Chapitre 2 - Potentiel électrique et condensateurs
Chapitre 2 - Potentiel électrique et condensateurs2.1 Travail et énergie2.1.1 Gravité vs. électrostatique2.1.2 Travail d'une force constanteDéfinition2.1.3 EnergieDéfinition2.1.4 Energie potentielle d'une forceDéfinition2.1.5 Gravité vs. électrostatiqueChamp gravifique2.1.6 Champ électrique2.1.7 Potentiel électriqueDéfinitionRemarques2.1.8 EquipotentiellesDéfinitionPropriété2.1.9 Différence de potentiel2.1.10 Energie d'une charge dans un champ électrique2.1.11 L'électronvolt comme unité d'énergie2.2 Condensateurs2.2.1 Concept de capacité2.2.2 Condensateur plan2.2.3 Condensateur cylindrique2.2.4 Association de condensateursCondensateurs en sérieCondensateurs en parallèle2.2.5 Condensateurs avec diélectriquesObservation macroscopiqueCondensateur planCondensateur cylindrique2.3 Diélectriques2.3.1 Description microscopique des diélectriques
2.1 Travail et énergie
2.1.1 Gravité vs. électrostatique
Le mouvement d'une charge
Une masse
Une charge
La seule différence majeure entre ces deux forces est que la gravitation n'est que attractive tandis que la force électrique peut aussi être répulsive.
=> L'accélération d'une masse à la surface de la Terre est toujours dirigée vers le bas.
2.1.2 Travail d'une force constante
Le travail d'une force mesure sa contribution à un déplacement.
Définition
Le travail
Le travail est une grandeur scalaire et son unité est le joule
Il est positif si
2.1.3 Energie
Définition
L'énergie est une grandeur physique abstraite qui demeure en quantité constante dans un système isolé (ne peut ni être créée, ni être détruite, elle se transforme). Elle peut se présenter sous forme cinétique, potentielle, chimique, thermique ou électromagnétique.
Si l'énergie
Energie = capacité d'effectuer un travail
2.1.4 Energie potentielle d'une force
Si une force
Définition
Dans le cas d'une force conservative, il existe une fonction
2.1.5 Gravité vs. électrostatique
Champ gravifique
Travail de
2.1.6 Champ électrique
Travail de
Cela montre que le travail
2.1.7 Potentiel électrique
Soit
avec
On a alors :
Définition
Soit
l'unité est le Volt
Remarques
- L'expression
- Le potentiel augmente quand on remonte une ligne de champ électrique et diminue quand on descend le long de celle-ci (indépendamment de
2.1.8 Equipotentielles
Définition
Tous les points de l'espace qui on le même potentiel électrique
Propriété
En tout point de l'espace, une surface équipotentielle est normale à la ligne de champ électrique passant par le point en question.
2.1.9 Différence de potentiel
Différence de potentiel entre deux points
Tension électrique entre deux points
Si
où
2.1.10 Energie d'une charge dans un champ électrique
Soit une charge
On suppose que la seule force qui s'exerce sur elle est la force électrique
D'après le théorème de l'énergie cinétique :
La variation de l'énergie cinétique d'une charge
En effet,
2.1.11 L'électronvolt comme unité d'énergie
L'unité SI de l'énergie est le Joule
Dans les problèmes liés à l'électrodynamique, l'énergie acquise ou perdue par une particule chargée se mesure avec des valeurs de d'un ordre de grandeur de
Ce n'est donc pas une unité très pratique en électromagnétisme.
On introduit alors une nouvelle unité, appelée électronvolt, définie par l'énergie acquise par un électron depuis le repos, par une différence de potentiel d'un volt :
2.2 Condensateurs
2.2.1 Concept de capacité
On appelle condensateur tout composant électrique constitué de deux conducteurs, appelés armatures, séparés par un isolant.
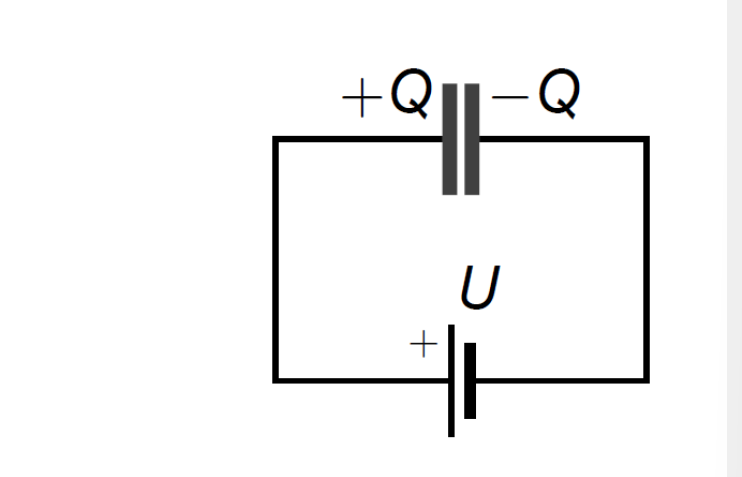
En appliquant une tension sur le condensateur (deux potentiels différents sur les armatures = différence de potentiel), on amène une charge
Dans cette configuration, les charges restent mieux en place : la perte de charges est limitée. Le condensateur peut donc être considérée comme un stockeur de charges.
La quantité de charges
La constante de proportionnalité
La capacité d'un condensateur dépend de la taille et de la géométrie des armature ainsi que du milieu isolant entre les armatures.
2.2.2 Condensateur plan
Les armatures sont planes et parallèles. Elles ont la même surface
La capacité d'un condensateurs plan est donnée par :
2.2.3 Condensateur cylindrique
Les armatures sont constituées de deux cylindres coaxiaux : le conducteur intérieur est un cylindre de longueur
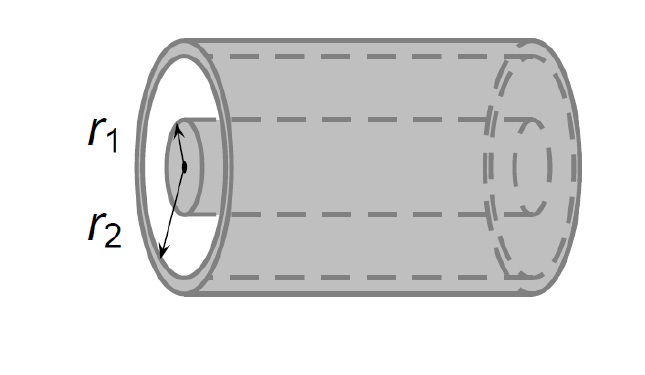
On suppose
La capacité d'un condensateur cylindrique est alors donnée par :
2.2.4 Association de condensateurs
Condensateurs en série
Chaque condensateur porte une charge
Condensateurs en parallèle
La tension
2.2.5 Condensateurs avec diélectriques
Un diélectrique est un milieu dans lequel les électrons ne peuvent pas se déplacer de manière macroscopique : c'est donc un isolant électrique
Observation macroscopique
Quand on introduit un diélectrique entre les armatures d'un condensateur, on observe que sa capacité augmente.
Sans diélectrique, sa capacité vaut
Avec un diélectrique, la charge entre les armatures ne change pas. En revanche, la tension va diminuer et vaudra
Dans ce cas, la capacité vaut :
On définit alors
Condensateur plan
Condensateur cylindrique
2.3 Diélectriques
2.3.1 Description microscopique des diélectriques
Entre les deux armatures d'un condensateur règne un champ électrique
Avec un diélectrique avec molécules polaires (eau) : les moments dipolaires des molécules ont tendance à s'orienter selon
Avec un diélectrique avec molécules non polaires : le champ extérieur crée des dipôles induits dans le diélectrique.
Dans les deux cas, les dipôles produisent un champ électrique induit
Plus
Un bon diélectrique n'est pas forcément un bon isolant :
Bon isolant
Bon diélectrique