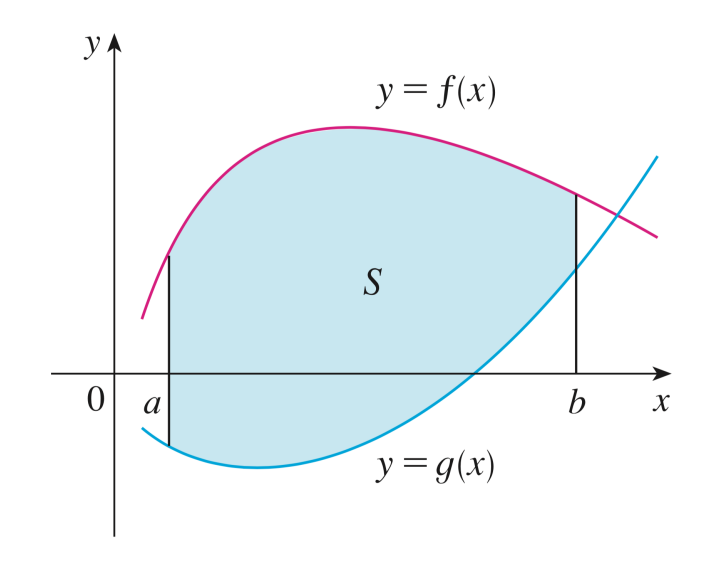
Soient \(f,g : \space [a,b] \longmapsto \mathbb{R}\) deux fonctions continue par morceaux telles que \(f(x) \geq g(x) \space \forall x \in [a,b]\). Soit
\[ S = \left\{ (x,y) \in \mathbb{R}^2 \space \vert \space a \leq x \leq b, \space g(x) \leq y \leq f(x) \right\} \]
la région bornée située entre les graphes de \(f\) et de \(g\) ainsi qu’entre les droites verticales d’équations \(x=a\) et \(x=b\). Alors l’aire \(A\) de la région \(S\) est donnée par :
\[ \boxed{\int_a^b \left(f(x) - g(x) \right) dx} \]

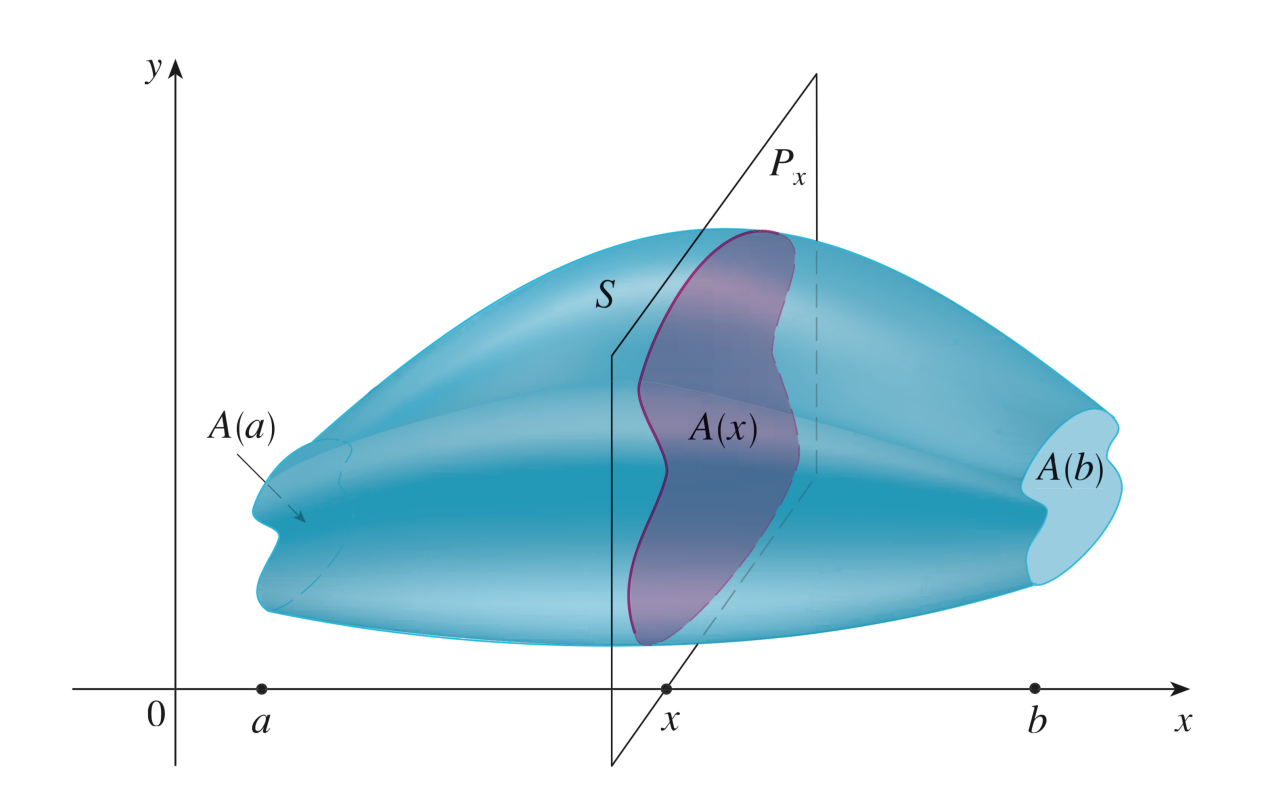
Soit \(S \subset \mathbb{R}^3\) un solide se trouvant entre \(x=a\) et \(x=b\) et soit \(P_x\) le plan perpendiculaire à l’axe \(x\) passant par le point \(x\). Soit \(A(x)\) l’aire de la section transversale \(S \cap P_x\). Le volume de \(S\) est alors défini par :
\[ \boxed{V=\int_a^b A(x)dx} \]
Un solide de révolution est un solide obtenu par rotation d’une région bornée du plan autour d’une droite.
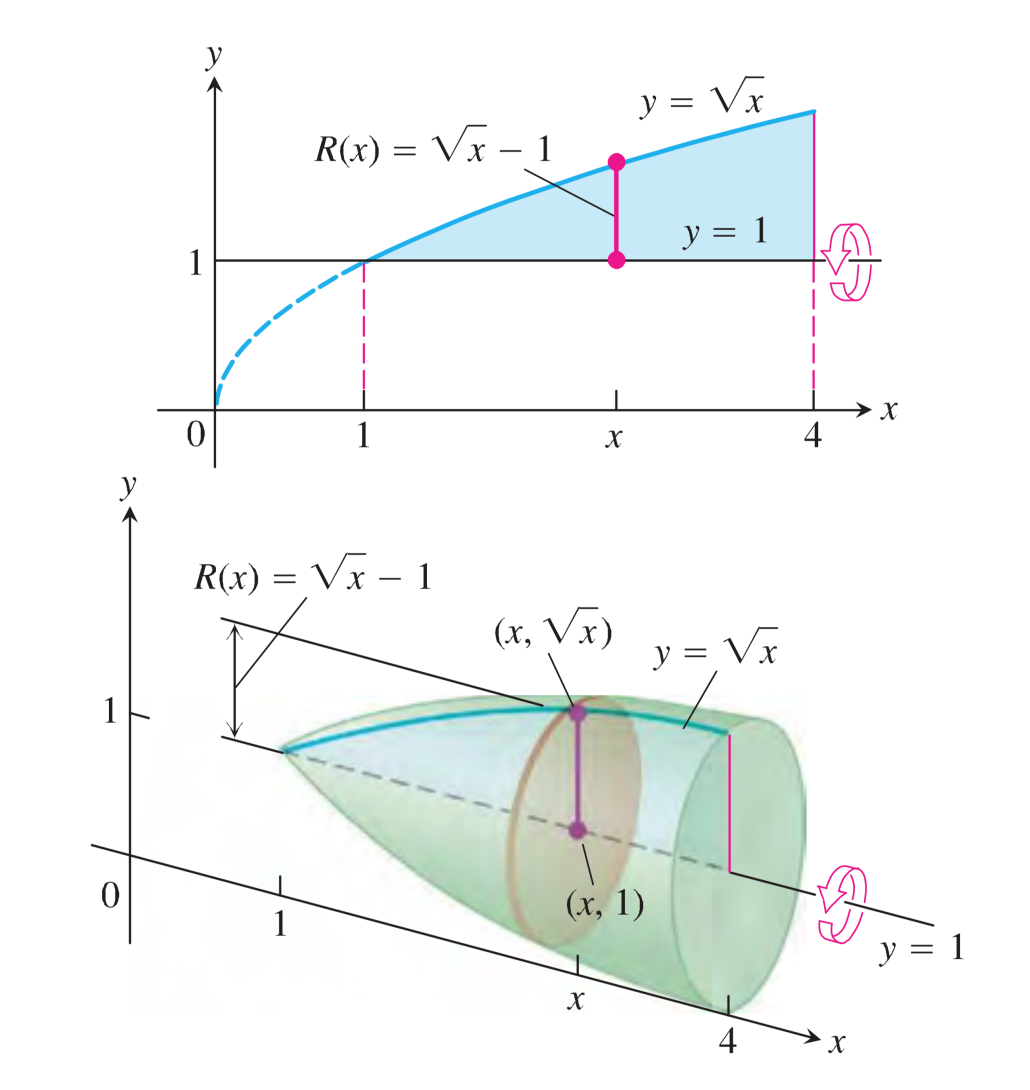
On fait tourner autour de la droite d’équation \(y=1\) la région bornée comprise entre la courbe d’équation \(y=\sqrt{x}\) et les droites d’équations \(y=1\) et \(x=4\). On cherche à calculer le volume du solide de révolution ainsi obtenu.
L’aire des sections transversales est donnée par :
\[ A(x) = \pi \cdot (R(x))^2 = \pi (\sqrt{x} -1) ^2 = \pi (x - 2\sqrt{x} + 1) \]
Ainsi, le volume est donné par :
\[ \begin{align*} V&=\int_1 ^4 A(x) dx = \int_1^4 \pi (x - 2\sqrt{x} + 1) dx\\ &= \pi \left[ \frac{1}{2} x^2 - \frac{4}{3} x^{3\over 2} + x \right]_1^4 = \frac{7}{6}\pi \end{align*} \]
Soit une courbe d’équation \(y=f(x)\) où \(f:\space [a,b]\longmapsto \mathbb{R}\) est une fonction dérivable dont la dérivée \(f'\) est continue par morceaux. La longueur de cette courbe est donnée par :
\[ \boxed{L=\int_a^b \sqrt{1+ ( f'(x)) ^2}\space \mathrm{d}x} \]
Une surface de révolution est une surface obtenue par une rotation d’une courbe d’équation \(y=f(x)\) autour d’une droite.

Soit une courbe d’équation \(y=f(x)\) où \(f:\space [a,b] \longmapsto [0,+\infty[\) est une fonction dérivable positive dont la dérivée \(f'\) est continue par morceaux. Soit \(S\) la surface de révolution obtenue après rotation de la courbe autour de l’axe \(x\). L’aire de \(S\) est donnée par :
\[ \boxed{A = \int _a^b 2\pi f(x) \sqrt{1 + \left( f'(x) \right)^2} \space\mathrm{d}x} \]
Exported with pandoc 2.9.2.1 on Wed Apr 27 2022 at 13:58:59 CEST. @ylked
All informations are given without warranty. All rights reserved ©