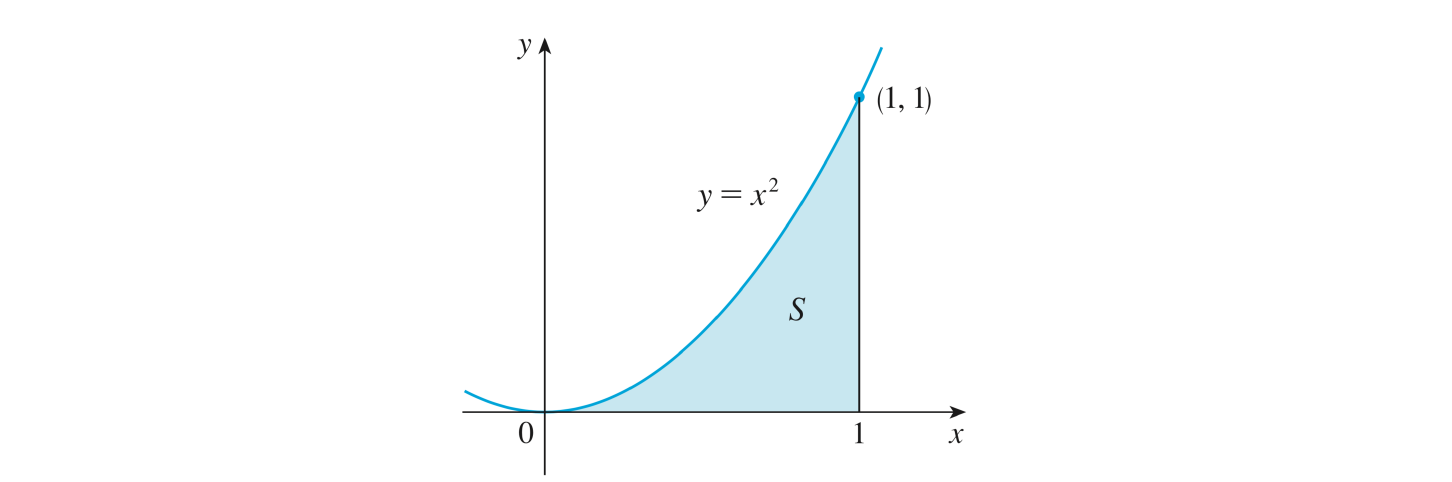
Soit la région
\[ S = \left\{ (x,y) \in \mathbb{R}^2 \vert \space 0 \leq x \leq 1 , 0 \leq y \leq x^2\right\} \]
de tous les points compris entre l’axe \(x\), la parabole d’équation \(y=x^2\) et les droites verticales d’équations \(x=0\) et \(x=1\). On cherche à déterminer l’aire \(A\) de la région \(S\).

Il est possible de subdiviser la région \(S\) en plusieurs rectangles (dont l’aire vaut base x hauteur) afin d’approximer l’aire \(A\).
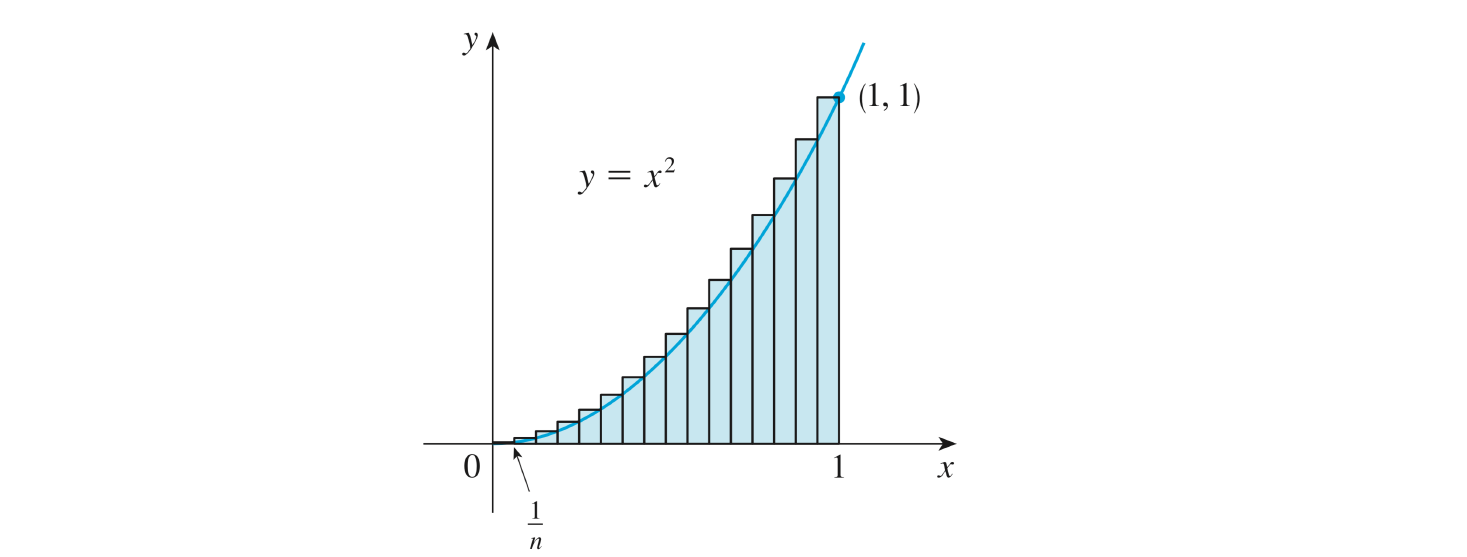
On représente dans le tableau suivant la valeur des approximations de l’aire \(A\) en fonction du nombre \(n\) de rectangles. On note \(G_n\) l’approximation à gauche et \(D_n\) l’approximation à droite.

On remarque que les approximations \(G_n\) sont croissantes tandis que \(D_n\) sont décroissantes. Toutes les deux semble tendre vers la même valeur \(\frac{1}{3}\) à mesure que \(n\) augmente. On définit alors l’aire \(A\) de la région \(S\) comme étant :
\[ A = \lim_{n\rightarrow\infty} G_n = \lim_{n\rightarrow\infty} D_n = \frac{1}{3} \]
En procédant de manière analogue à l’exemple 4.1.1, on peut calculer l’aire de la région :
\[ S = \left\{\left( x,y\right) \in \mathbb{R} ^2 \vert \space a \leq x \leq b, \space 0\leq y \leq f(x) \right\} \]
comprise entre l’axe \(x\), les droites verticales d’équations \(x=a\) et \(x=b\) et le graphe d’une fonction \(f\) continue et positive quelconque.
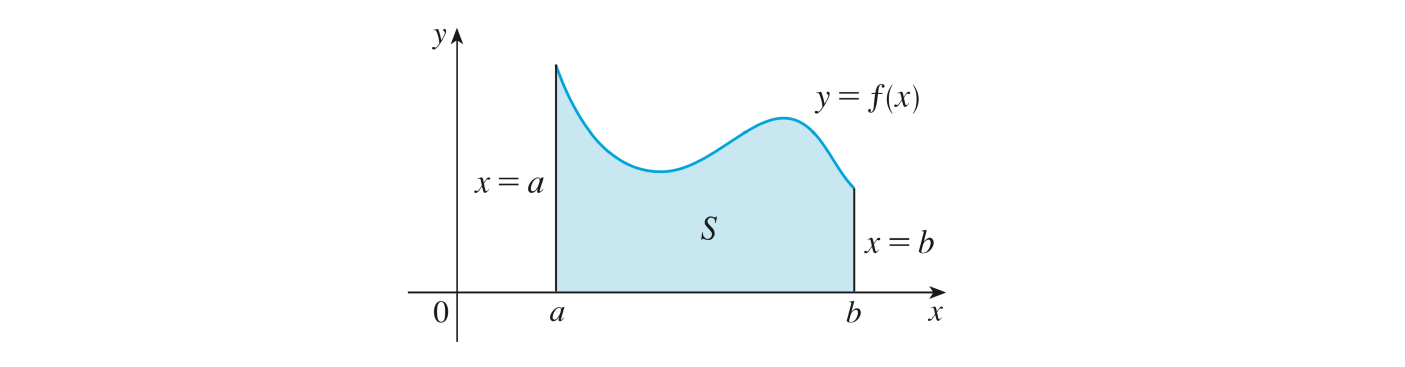
On décompose la surface \(S\) en \(n\) sous-intervalles de même largeur :
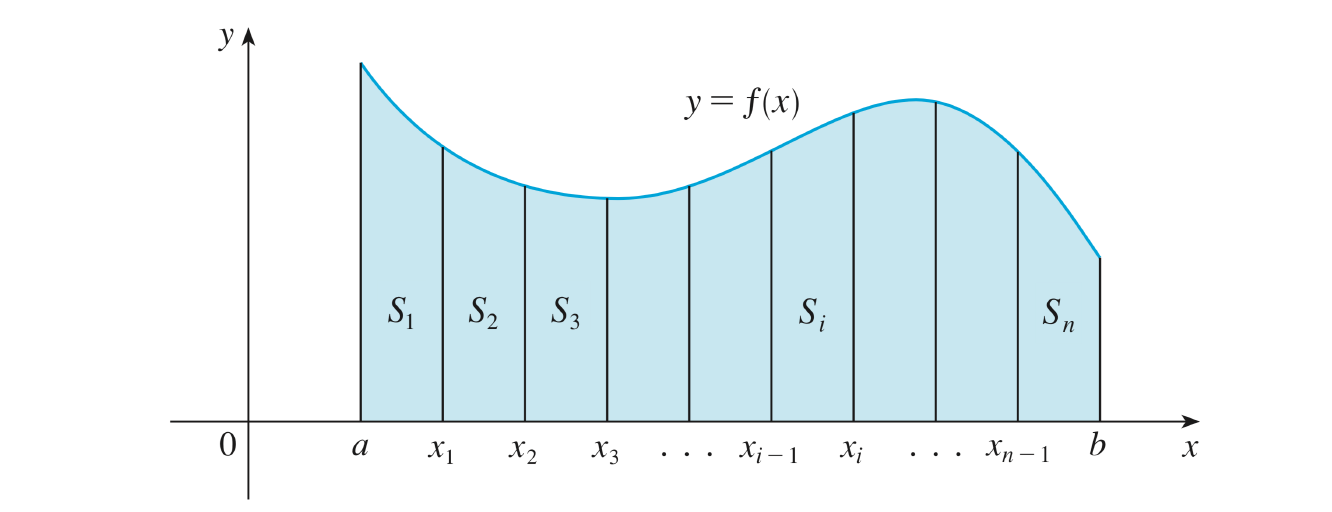
Comme la longueur totale de l’intervalle \(\left[a,b\right]\) vaut \(b-a\), chaque sous-intervalle aura une largeur définie par :
\[ \Delta x = \frac{b-a}{n} \]
Les \(n\) sous-intervalles sont alors définis par :
\[ [x_0,x_1], [x_1,x_2], [x_2,x_3], ..., [x_{n-1} ,x_n] \]
où
\[ \begin{align} x_0 &= a\\ x_1 &= a + \Delta x\\ x_2 &= a + 2\Delta x\\ \vdots\\ x_n &= a + n\Delta x = a + n \cdot \frac{b-a}{n} = b \end{align} \]
L’approximation de l’aire à droite de la région \(S\) est donnée par la somme des \(n\) rectangles \(S_1,S_2, ... ,S_n\), des rectangles de même largeur et de hauteur égale au coin supérieur droit de chaque tranche :
\[ D_n = f(x_1) \cdot \Delta x + f(x_2) \cdot \Delta x + ... + f(x_n) \cdot \Delta x = \sum_{i=1}^{n} f(x_i) \cdot \Delta x \]
L’aire totale \(A\) de la surface \(S\) est alors définie comme étant la limite des approximations à droite (ou à gauche) \(D_n\) lorsque \(n\rightarrow \infty\) :
\[ \boxed{ \quad \begin{align} A &= \lim_{n\rightarrow \infty} \left( \sum_{i=1}^{n} f(x_i) \cdot \Delta x \right) \end{align} \quad} \]
Une fonction \(f : [a,b] \longmapsto \mathbb{R}\) est dite continue par morceaux si elle possède au plus un nombre fini de points en lesquels elle est discontinue mais pour lesquels les limites à gauche et à droite existent et ne sont pas infinies.
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. L’intégrale définie de \(f\) entre \(a\) et \(b\) est le nombre noté et défini par :
\[ \int_a^b f(x)\mathrm{d}x = \lim_{n\rightarrow \infty} \left( \sum_{i=1}^{n} f(x_i) \cdot \Delta x \right) \]
où
\[ \begin{align} x_0 &= a\\ x_1 &= a + \Delta x\\ x_2 &= a + 2\Delta x\\ \vdots\\ x_n &= a + n\Delta x = a + n \cdot \frac{b-a}{n} = b \end{align} \]
Dans le cas où la fonction \(f\) prend à la fois des valeurs positives et négatives, alors la somme \(\sum_{i=1}^{n} f(x_i) \cdot \Delta x\) additionne les aires au dessus de l’axe \(x\) et soustrait les aires en dessous.
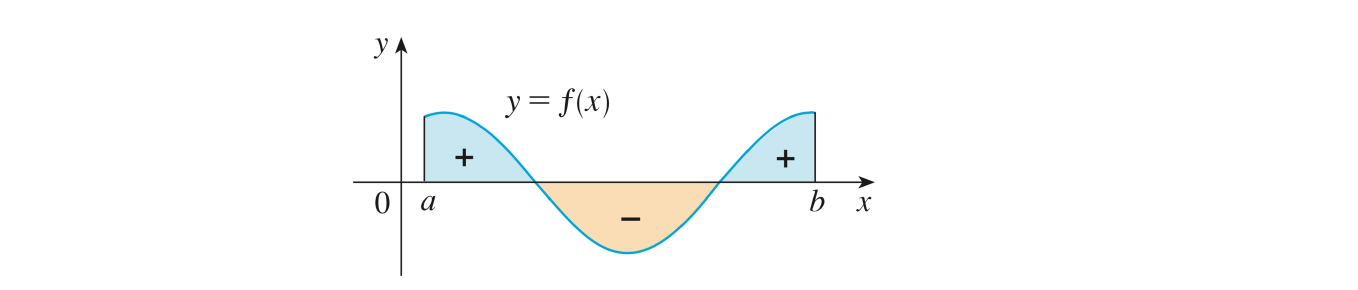
Soit \(f : [a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. On a alors :
\[ \boxed{ \quad \int_b^a f(x)\mathrm{d}x = -\int_a^b f(x)\mathrm{d}x \quad} \]
Pour toute fonction telle que \(f(a)\) existe, on a :
\[ \boxed{ \quad \int_a^a f(x)\mathrm{d}x = 0 \quad} \]
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux et soit \(c \in \mathbb{R}\) une constante. Alors :
\[ \boxed{ \quad \int_a^b c \cdot f(x) \mathrm{d}x = c \cdot \int_a^b f(x)\mathrm{d}x \quad} \]
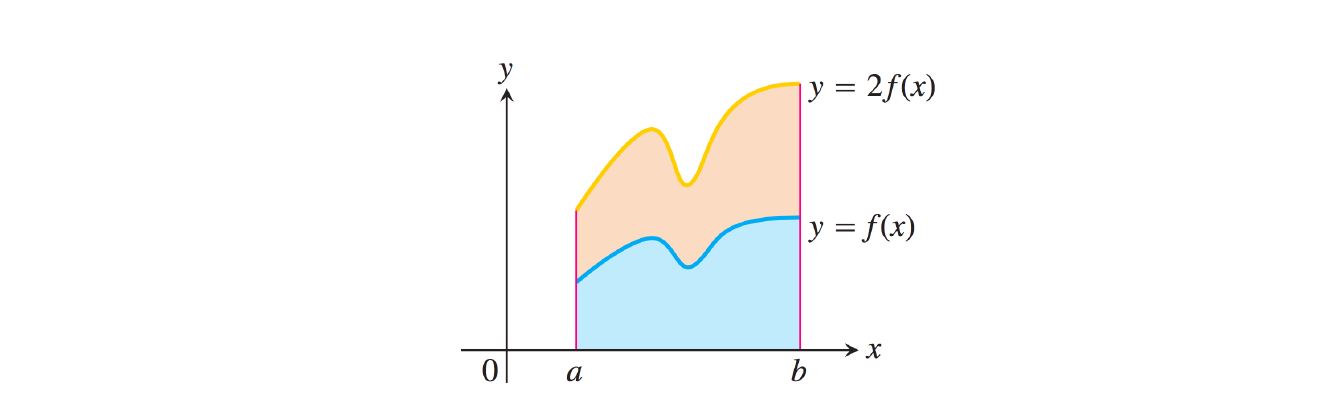
Soient \(f,g : [a,b] \longmapsto \mathbb{R}\) deux fonctions continues par morceaux. Alors
\[ \boxed{ \quad \int_a^b \left(f(x) + g(x)\right) \mathrm{d}x = \int_a^b f(x) \mathrm{d}x + \int_a^b g(x)\mathrm{d}x \quad} \]
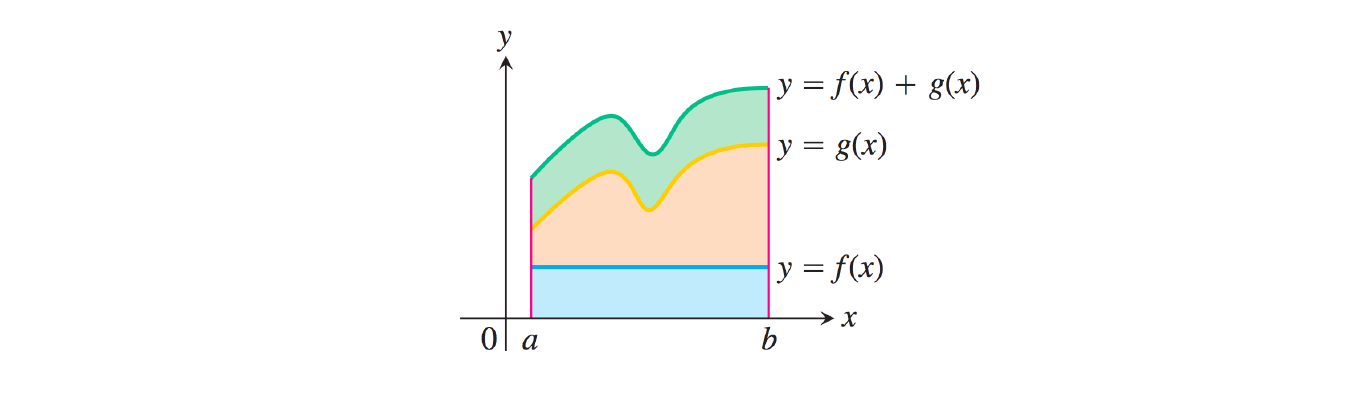
Soit \(f:[a,c] \longmapsto \mathbb{R}\) une fonction continue par morceaux et soit \(b \in [a,c]\). Alors :
\[ \boxed{ \quad \int_a^c f(x)\mathrm{d}x = \int_a^b f(x) \mathrm{d}x + \int _b^c f(x)\mathrm{d}x \quad} \]
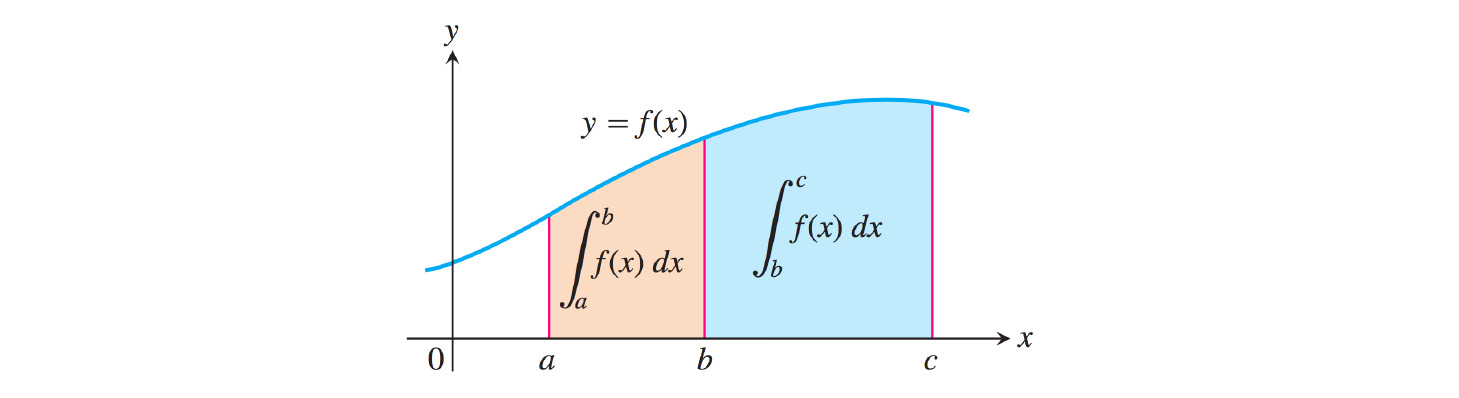
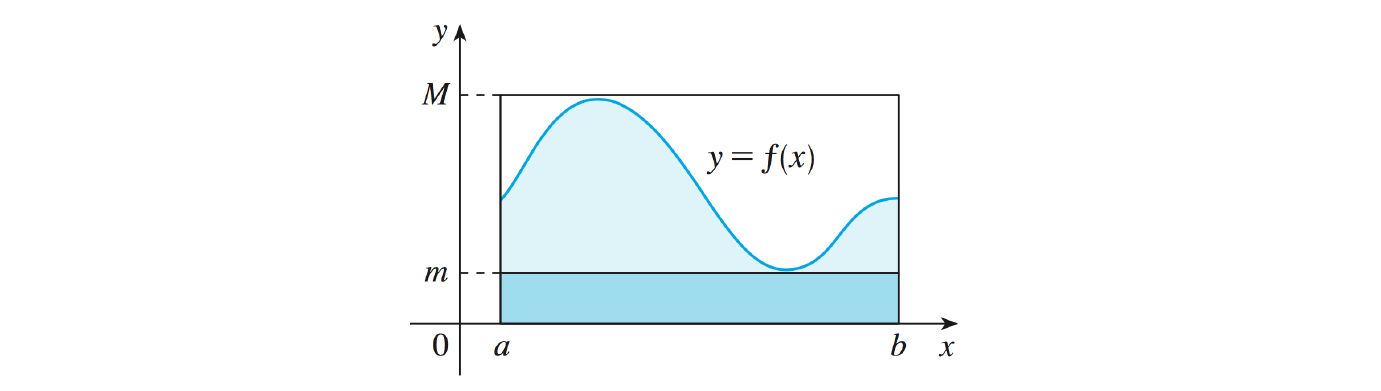
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux telle que \(\forall x \in [a,b]\), on a \(m \leq f(x) \leq M\). Alors :
\[ \boxed{ \quad m(b-a) \leq \int_a^b f(x)\mathrm{d}x \leq M(b-a) \quad} \]
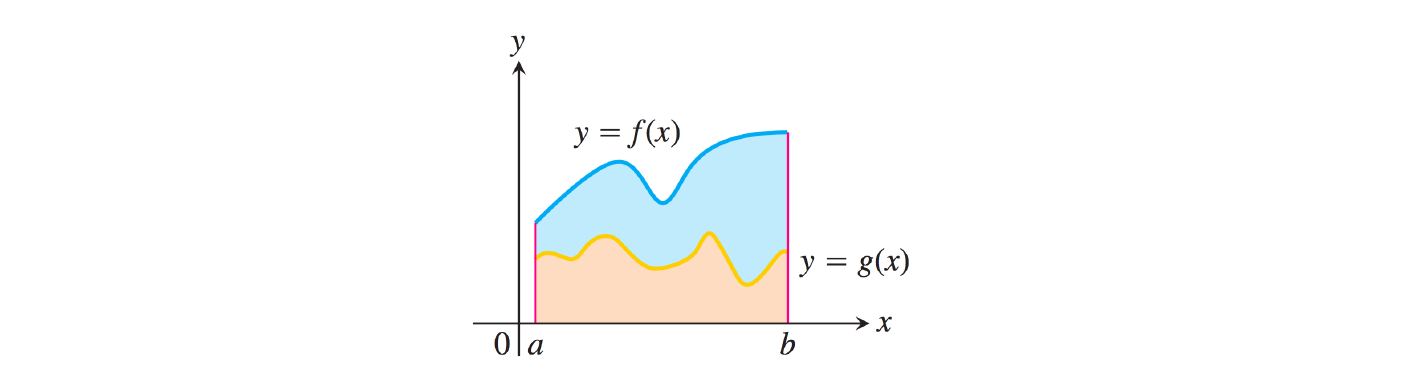
Soient \(f,g:[a,b] \longmapsto \mathbb{R}\) deux fonction continues par morceaux telles que \(f(x) \geq g(x) \quad \forall x \in [a,b]\). Alors :
\[ \boxed{ \quad \int_a^b f(x) \mathrm{d}x \geq \int_a^b g(x)\mathrm{d}x \quad} \]
Soit \(f:[-a,a] \longmapsto \mathbb{R}\) une fonction continue par morceaux.
Si \(f\) est paire, alors :
\[ \boxed{ \quad \int_{-a}^a f(x) \mathrm{d}x = 2\int_{0}^af(x)\mathrm{d}x \quad} \]
Si \(f\) est impaire, alors :
\[ \boxed{ \quad \int_{-a}^a f(x)\mathrm{d}x = 0 \quad} \]
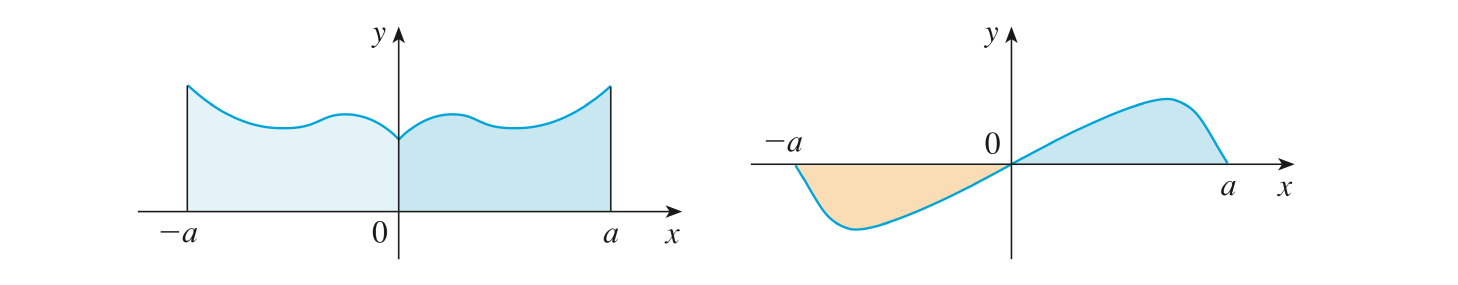
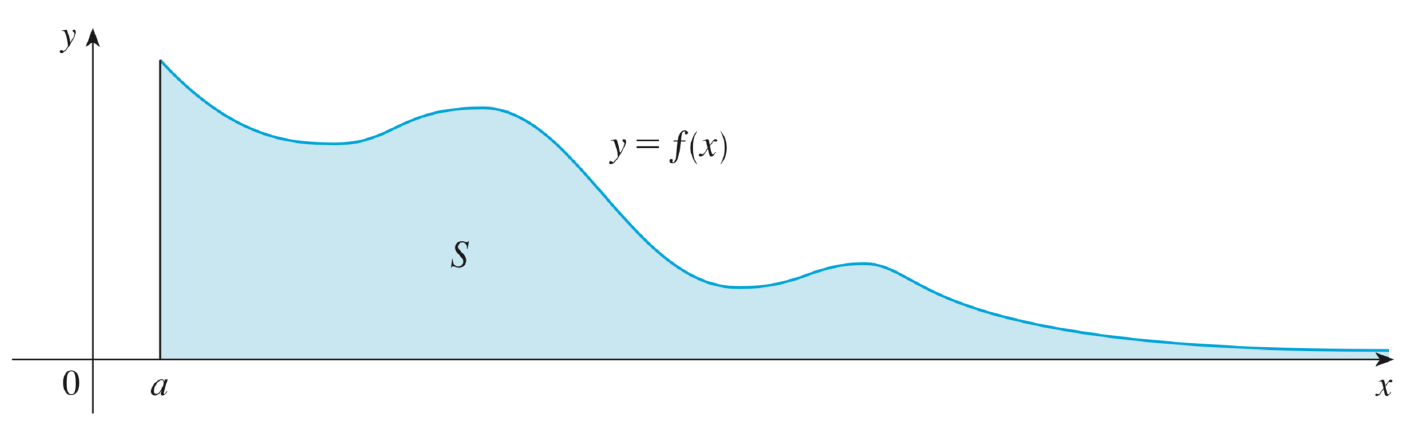
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. Soit la fonction :
\[ A(x) = \int_a^xf(t)dt \]
La variable est ici la borne supérieure de l’intégrale définie. Ainsi, pour chaque valeur de \(x \in [a,b]\) , on obtient une valeur \(A(x)\), \(A\) est donc bien une fonction de \(x\).
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. Alors la fonction
\[ A(x) = \int_a^x f(t)dt \]
est dérivable et sa dérivée vaut
\[ A'(x) = f(x) \]
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. Une primitive de \(f\) est une fonction \(F:[a,b] \longmapsto \mathbb{R}\) telle que \(F'(x) = f(x) \space, \quad \forall x \in [a,b]\).
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux et soit \(F\) une primitive de \(f\). Alors toutes les primitives de \(f\) sont de la forme :
\[ F(x) + C \]
Où \(C \in \mathbb{R}\) est une constante.
Le théorème nous dit alors que toutes les primitives d’une même fonction ne diffèrent que d’une constante.
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux. L’intégrale indéfinie de \(f\) est l’ensemble de toutes les primitives de \(f\) et est noté :
\[ \int f(x)\mathrm{d}x \]
Soient \(f,g : [a,b] \longmapsto \mathbb{R}\) deux fonctions continues par morceaux. Alors :
\[ \begin{align*} 1. & \quad\int \left( f(x) + g(x) \right)\mathrm{d}x = \int f(x)\mathrm{d}x + \int g(x)\mathrm{d}x\\\\ 2. & \quad \int \lambda \cdot f(x)\mathrm{d}x = \lambda \cdot \int f(x)\mathrm{d}x \end{align*} \]
\[ \boxed{ \quad \begin{align*} 1. \quad& \int x^n \mathrm{d}x = \frac{x^{n+1}}{n+1} + C \quad\text{ si } n \neq 1 \\\\ 2. \quad & \int \frac{1}{x} \mathrm{d}x = \ln{\vert x \vert} + C \\\\ 3. \quad & \int e^x \mathrm{d}x = e^x + C \\\\ 4. \quad & \int a^x \mathrm{d}x = \frac{a^x }{\ln a} + C \\\\ 5. \quad & \int \sin x \mathrm{d}x = -\cos x + C \\\\ 6. \quad & \int \cos x \mathrm{d}x = \sin x + C \\\\ 7. \quad & \int \frac{1}{\sin ^2 x}\mathrm{d}x = \tan x + C \\\\ 8. \quad & \int \frac{1}{x^2 + 1} \mathrm{d}x = \arctan x + C \\\\ 9. \quad & \int \frac{1}{\sqrt{1-x^2}}\mathrm{d}x = \arcsin x + C \end{align*} \quad} \]
Soit \(f:[a,b] \longmapsto \mathbb{R}\) une fonction continue par morceaux et soit \(F:[a,b] \longmapsto \mathbb{R}\) une primitive de \(f\). Alors
\[ \boxed{ \quad \int_a^b f(x) \mathrm{d}x = F(b) - F(a) \quad} \]
Soit \(f\) une fonction continue par morceaux et soit \(g\) une fonction dérivable ayant une dérivée continue par morceaux. Alors :
\[ \boxed{ \quad \int f(g(x))\cdot g'(x) \mathrm{d}x = \int f(u)du \quad} \]
où \(u=g(x)\) et \(du = g'(x)\mathrm{d}x\).
Soit \(f\) une fonction continue par morceaux et soit \(g\) une fonction dérivable ayant une dérivée continue par morceaux. Alors :
\[ \boxed{ \quad \int_a^b f(g(x)) \cdot g'(x)\mathrm{d}x = \int_{g(a)} ^{g(b)} f(u)du \quad} \]
Soient \(u\), \(v\) deux fonctions dérivables ayant des dérivées continues par morceaux. Alors :
\[ \boxed{ \quad \int u \cdot v'\space \mathrm{d}x = u \cdot v - \int u' \cdot v \space \mathrm{d}x \quad} \]
En appliquant le TFC2 à la formule d’intégration par parties, on obtient le théorème suivant :
Soient \(u,v : [a,b] \longmapsto \mathbb{R}\) deux fonctions dérivables ayant des dérivées continues par morceaux. Alors :
\[ \boxed{\quad \int_a ^b u \cdot v' \space \mathrm{d}x = u \cdot v {\Big|_{a}} ^b - \int _a ^b u' \cdot v \space \mathrm{d}x \quad} \]
Il n’existe pas de méthode directe pour intégrer une toute fonction rationnelle. Cependant, on connait l’intégrale indéfinie de certaines fonctions rationnelles particulières :
\[ \begin{align} & \int \frac{1}{ax + b} \mathrm{d}x = \frac{1}{a}\cdot \ln \vert ax + b \vert + C \\\\ & \int \frac{1}{x^2 + a^2}\mathrm{d}x = \frac{1}{a} \cdot \arctan{\left( \frac{x}{a}\right)} + C \end{align} \]
L’idée est alors de décomposer toute fonction rationnelle en une somme de fonction rationnelles d’une des deux formes ci-dessus. On appelle cette décomposition la décomposition en éléments simples.
Soit \(f\) une fonction rationnelle telle que :
\[ f(x) = \frac{P(x)}{Q(x)} \]
Si \(\deg P \geq \deg Q\), on effectue la division polynomiale pour écrire \(f\) sous la forme suivante :
\[ f(x) = S(x) + \frac{R(x)}{Q(x)} \]
où \(\deg R < \deg Q\)
Ensuite, il faut factoriser au maximum le dénominateur \(Q(x)\)
Si \(Q(x)\) se factorise en un produit de \(k\) facteurs de degré 1 tous distincts :
\[ Q(x) = (a_1 x + b_1)(a_2 x + b_2) ... (a_k x + b_k) \]
il faut chercher des constantes \(A_1, \space A_2, ... , A_k\) telles que
\[ \frac{R(x)}{Q(x)} = \frac{A_1}{a_1 x + b_1} + \frac{A_2}{a_2 x + b_2} + ... + \frac{A_k}{a_k x + b_k} \]
Si un des facteurs de \(Q(x)\) est un facteur de multiplicité \(r\) du type \((a_i x + b_i) ^r\) , on ajoute à la décomposition en éléments simples les éléments suivants :
\[ \frac{A_1}{a_i x + b_i} + \frac{A_2}{(a_i x+ b_i)^2} + ... + \frac{A_r}{(a_i x + b_i)^r} \]
Si un des facteurs de \(Q(x)\) est un facteur irréductible du type \((ax^2 + bx + c)\) où \(b^2 -4ac < 0\) , on ajoute à la décomposition en facteurs simples le terme suivant :
\[ \frac{Ax + B}{ax^2 + bx + c} \]
Si un des facteurs de \(Q(x)\) est un facteur irréductible de multiplicité \(r\) du type \((ax^2 + bx + c)^r\) où \(b^2-4ac<0\) , on ajoute à la décomposition en éléments simples les termes suivants :
\[ \frac{A_1x + B_1}{ax^2 + bx + c} + \frac{A_2x + B_2}{(ax^2 + bx + c)^2} + ... + \frac{A_kx + B_k}{(ax^2 + bx + c)^r} \]
Simplifier l’intégrande autant que possible.
Cherche un changement de variable évident.
Chercher des facteurs \(u\) et \(v'\) évidents pour intégrer par parties.
Si l’intégrande est une fonction rationnelle, utiliser la méthode de décomposition en éléments simples.
Essayer à nouveau :
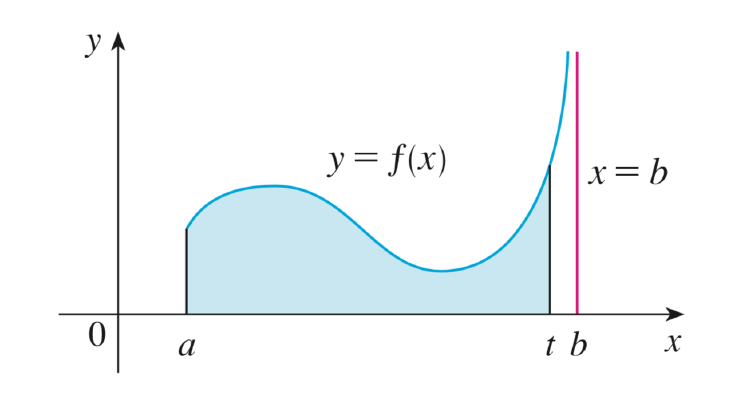
Soit \(f : \mathbb{R} \longmapsto \mathbb{R}\) une fonction continue par morceaux. Alors :
\[ \int _a ^{+\infty} f(x) dx = \lim_{t\rightarrow +\infty}\int _a^t f(x) dx \]
et
\[ \int _{-\infty} ^{b} f(x) dx = \lim_{t\rightarrow -\infty}\int _t^b f(x) dx \]
(si ces limites existent). De plus, si pour une certaine valeur \(a \in \mathbb{R}\) , les intégrales impropres suivante existent :
\[ \int _{-\infty}^a f(x)dx \quad \text{ et } \quad \int_a^{+\infty} f(x)dx \]
alors :
\[ \int_{-\infty}^{+\infty}f(x)dx = \int _{-\infty}^a f(x)dx + \int_{a}^{+\infty} f(x)dx \]
Soit \(f\) une fonction possédant en \(x=b\) une discontinuité de type infini et soient \(a<b<c\). Alors :
\[ \int _a^b f(x)dx = \lim _{t\rightarrow b^-} \int _a^t f(x) dx \]
et
\[ \int _b^c f(x)dx = \lim _{t\rightarrow b^+} \int _t ^c f(x)dx \]
(Si ces limites existent). De plus, si les intégrales impropres ci-dessus existent, alors :
\[ \int _a^c f(x)dx = \int _a^b f(x)dx + \int _b ^c f(x) dx \]
Exported with pandoc 2.9.2.1 on Thu Mar 17 2022 at 13:10:26 CET. @ylked
All informations are given without warranty. All rights reserved ©