
[TOC]
On cherche à définir la tangente à une courbe quelconque.
Soit une courbe d’équation \(y=f(x)\). On désire alors trouver la pente \(m\) de la tangente à la courbe en un point \(P(a, f(a))\). On choisi alors un point \(Q(x, f(x))\) proche de \(P\) et on calcule la pente \(m_{PQ}\) de la sécante passant par \(P\) et \(Q\).
On a alors : \[
m_{P,Q} = \frac{f(x)-f(a)}{x-a}
\] 
En faisant tendre \(Q\) vers \(P\), on fait tendre la pente de la sécante vers la pente de la tangente en \(P\).
Ainsi, la pente \(m\) de la limite vaut : \[
m = \lim_{x\rightarrow a}m_{PQ} = \lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}
\] 
La droite tangente au graphe de la fonction \(f\) au point \(P(a, f(a))\) est la droite passant par \(P\) et de pente : \[ \boxed{ \quad m = \lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a} \quad} \] (Dans le cas où cette limite existe).
Soit \(f : D \longmapsto \R\) une fonction et soit \(a \in D\). La dérivée de la fonction \(f\) en \(a\) est notée \(f'(a)\) et est définie par : \[ \boxed{ \quad f'(a) = \lim_{x\rightarrow a} \frac{f(x)-f(a)}{x-a} \quad} \] On voit alors que :
La dérivée \(f'(a)\) d’une fonction \(f\) en \(a\) est égale à la pente de la tangente au graphe de \(f\) au point \(P(a, f(a))\).
Soit \(f : D \longmapsto \R\) une fonction et soit \(a \in D\). Alors : \[ f'(a) = \lim_{x\rightarrow a} \frac{f(x)-f(a)}{x-a} = \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} \] (Dans le cas où ces limites existent).
Considérons un objet se déplaçant en ligne droite. La position \(s\) de l’objet au temps \(t\) est donnée par \(s=f(t)\).
La fonction \(f\) est appelée la fonction position de l’objet. Durant l’intervalle de temps \(\Delta t = h\) entre \(t=a\) et \(t=a + h\), la variation de la position de l’objet est donnée par \[
\Delta s = f(a+h)-f(a)
\] 
La vitesse moyenne de l’objet sur cette intervalle de temps est donnée par : \[ v_{moy} = \frac{\Delta s}{\Delta t} = \frac{f(a+h)-f(a)}{h} \] En faisant tendre \(h\) vers 0, on obtient la vitesse instantanée \(v(a)\) de l’objet au temps \(t=a\).
Soit \(f(t)\) la fonction décrivant la position au temps \(t\) d’un objet se déplaçant en ligne droite. La vitesse instantanée \(v(a)\) de l’objet au temps \(t=a\) est donnée par : \[ \boxed{ \quad v(a) = \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} = f'(a) \quad} \]
La vitesse instantanée \(v(a)\) d’un objet au temps \(t=a\) est égale à la dérivée \(f'(a)\) de la fonction position \(f\) au temps \(t=a\).
Soit \(f\) une fonction. La fonction dérivée de \(f\) (ou dérivée de \(f\)) est la fonction notée \(f'\) et définie par : \[ \boxed{ \quad f'(x) = \lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h} \quad} \]
Une fonction \(f\) est dérivable en \(a\) si et seulement si \(f'(a) \in \R\).
Cela signifie qu’elle est dérivable en \(a\) si la limite suivante existe et est différente de \(\pm \infty\) : \[ f'(a) = \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} \]
Une fonction \(f\) est dérivable en \(a\) si le graphe de \(f\) possède une tangente non verticale en \(x=a\).
Si une fonction \(f\) est dérivable en \(a\), alors elle est continue en \(a\).
Si une fonction n’est pas continue en \(a\), elle n’est pas dérivable en \(a\).
Attention : la réciproque est fausse :
Il existe des fonctions continues en \(a\) non dérivable en \(a\).
Soit \(f\) une fonction non dérivable en un point \(x=a\). On dit que \(f\) possède :
Un point de non dérivabilité de type discontinuité si :
\(f\) est discontinue en \(a\).
Un point de non dérivabilité de type point anguleux si
la dérivée \(f'\) possède une discontinuité de type saut en \(a\).
Un point de non dérivabilité de type point à tangente verticale si
la dérivée \(f'\) possède une discontinuité de type infinie en \(a\).
Il existe différentes notations pour les dérivées. La dérivée d’une fonction \(y=f(x)\) peut se noter : \[ f'(x) = y' = \frac{df}{dx} = \frac{dy}{dx} \] L’évaluation de la fonction dérivée en un point \(x=a\) se note alors : \[ f'(a) = y'(a) = \frac{df}{dx}\Bigg|_ {x=a} = \frac{dy}{dx} \Bigg | _ {x=a} \]
Soit \(f : D \longmapsto \R\) une fonction et soit \(I \sub D\) un intervalle.
La fonction \(f\) est dite croissante sur l’intervalle \(I\) si \[ f(x_1) \leq f(x_2) \quad\text{lorsque } x_1 < x_2 \text{ et } x_1,x_2 \in I \] La fonction \(f\) est dite décroissante sur l’intervalle \(I\) si \[ f(x_1) \geq f(x_2) \quad\text{lorsque } x_1 < x_2 \text{ et } x_1,x_2 \in I \]
Soit \(f : D \longmapsto \R\) une fonction dérivable et soit \(I\sub D\) un intervalle.
Si \(f'(x) \geq 0\quad \forall x \in I\) , alors \(f\) est croissante sur \(I\).
Si \(f'(x)\leq 0 \quad \forall x \in I\) , alors \(f\) est décroissante sur \(I\).
La dérivée d’une fonction \(f\) constante vaut \(f'(x)=0\).
Soit \(f\) une fonction puissance de la forme \(f(x)=x^n, \quad n \in \N\).
La fonction dérivée de \(f\) est alors donnée par : \[ \boxed{ \quad \frac{d}{dx} x^n = nx^{n-1} \quad} \]
On se rend compte que le théorème 3.3.2 reste valable pour toute fonction de la forme \(f(x)=x^s , \quad s \in \R\).
Soit \(f\) une fonction puissance de la forme \(f(x)=x^s, \quad s \in \R\).
La fonction dérivée de \(f\) est alors donnée par : \[ \boxed{ \quad \frac{d}{dx} x^s = sx^{s-1} \quad} \]
Soient \(f\) et \(g\) deux fonctions et \(c \in \R\) une constante. Alors : $$ \[\begin{align} &1. \quad \frac{d}{dx} [c \cdot f(x)] = c \cdot \frac{d}{dx} f(x) \\\\ &2. \quad \frac{d}{dx} [f(x) + g(x)] = \frac{d}{dx} f(x) + \frac{d}{dx} g(x) \end{align}\] $$
Pour trouver la fonction dérivée d’une fonction polynomiale, il suffit alors de la décomposer en une somme de fonctions puissances et de les dériver individuellement.
La dérivée d’une fonction exponentielle est proportionnelle à la fonction elle-même
La dérivée de la fonction exponentielle naturelle \(e^x\) est la fonction exponentielle naturelle elle-même : \[
\boxed{ \quad
\frac{d}{dx} e^x = e^x
\quad}
\] 
La dérivée de la fonction exponentielle \(a^x\) vaut : \[ \boxed{ \quad \frac{d}{dx} a^x = \ln (a) \cdot a^x \quad} \]
Dans le tableau suivant sont listées les dérivées de certaines fonctions élémentaires.
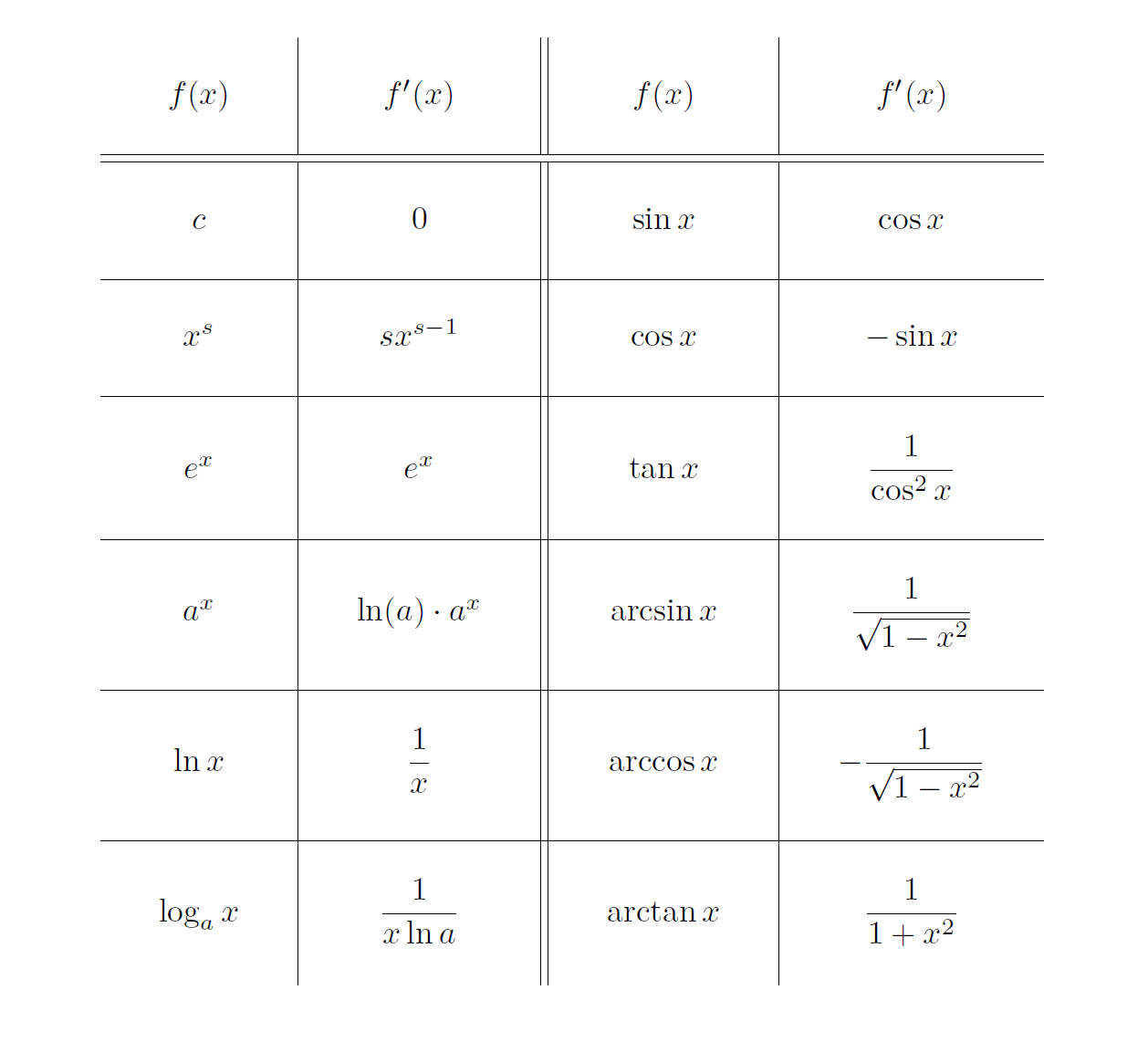
Contrairement à la dérivée d’une somme, la dérivée d’un produit n’est pas le produit des dérivées !
Soient \(u\) et \(v\) deux fonctions dérivables. Alors \[ \boxed{ \quad (u \cdot v)' = u' \cdot v + u \cdot v' \quad} \]
Soient \(u\) et \(v\) deux fonctions dérivables. Alors \[ \boxed{ \quad \left(\frac{u}{v}\right)' = \frac{u' \cdot v - u \cdot v'}{v^2} \quad} \]
Soient \(u\) une fonction dérivable en \(x\) et \(u\) une fonction dérivable en \(v(x)\). Alors la fonction composée \(u \circ v\) est dérivable en \(x\) et on a : \[ \boxed{ \quad \left( u \circ v\right)'(x) = u'(v(x)) \cdot v'(x) \quad} \] Le théorème 3.5.1 affirme que la dérivée d’une fonction composée est égale à la dérivée de la fonction extérieure multipliée par la dérivée de la fonction intérieure.
| intitulé | expression |
|---|---|
| produit fonction-constante | \((c \cdot u)'= c \cdot u'\) |
| somme | \((u+v)' = u' + v'\) |
| produit | \((u \cdot v)' = u' \cdot v + u \cdot v'\) |
| quotient | $() = $ |
| composition de fonctions | \((u \circ v)'(x) = u'(v(x)) \cdot v'(x)\) |

Si \(f\) est une fonction dérivable, alors la fonction dérivée \(f'\) est elle-même une fonction qui pourrait être dérivable à son tour. Si c’est le cas, on obtient en dérivant \(f'\) une nouvelle fonction \(f''\) appelée deuxième dérivée de \(f\).
Soit \(f\) une fonction dérivable dont la dérivée \(f'\) est elle même dérivable. La deuxième dérivée de \(f\) est la fonction notée \(f''\) qui est la dérivée de \(f'\).
Dans la notation de Leibniz, on note : \[ \frac{d^2f}{dx^2} \]
Soit \(f\) une fonction deux fois dérivable sur un intervalle \(I\). On dit que :
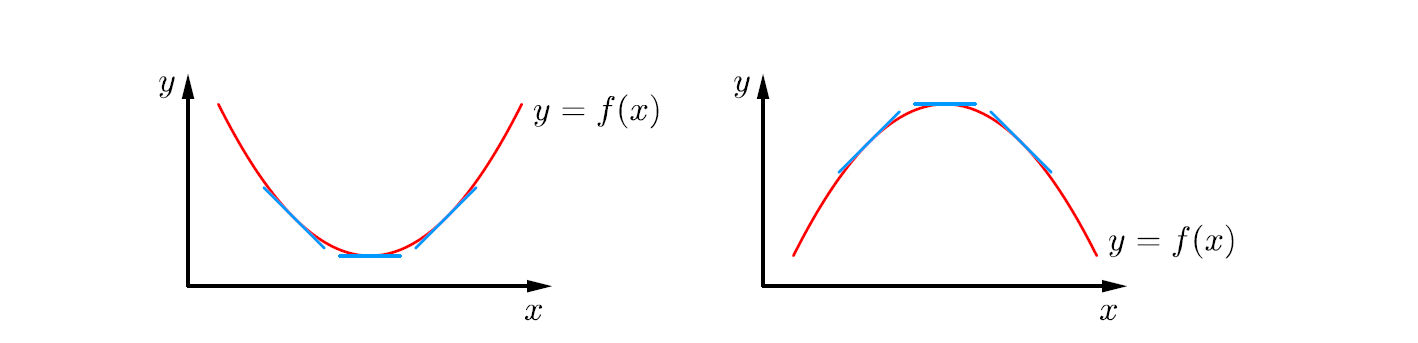
Sur la figure suivante est représenté le graphe d’une fonction \(f\) qui est convexe sur l’intervalle \([a,b]\) et qui est concave sur l’intervalle \([b,c]\). Le point \(P(b,f(b))\) est donc l’endroit où la fonction passe de convexe à concave. Un tel point est appelé un point d’inflexion. On constate que le graphe de la fonction traverse sa tangente en un tel point.
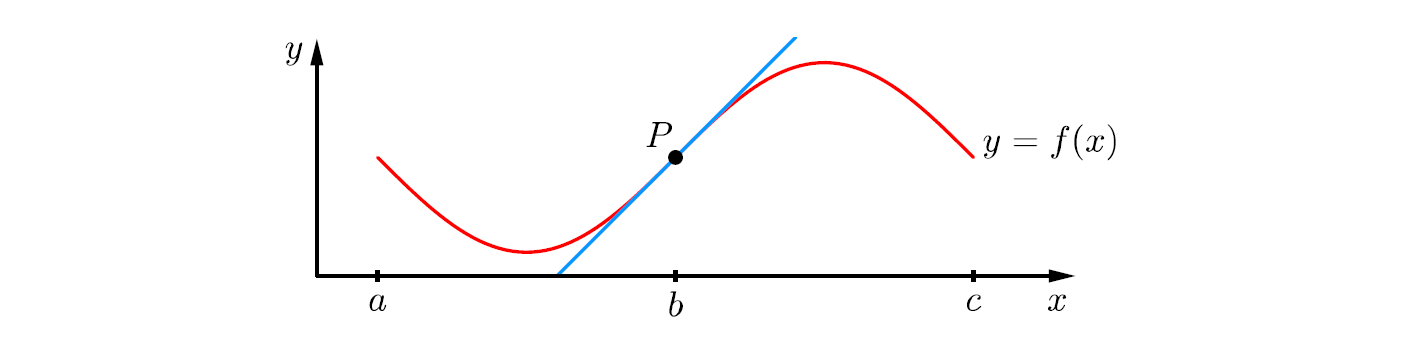
Soit \(f : D \longmapsto \R\) une fonction possédant une tangente en un point \(c \in D\). On dit que \(f\) possède un point d’inflexion en \(x=c\) si \(f\) passe de convexe à concave ou de concave à convexe en \(x=c\).
Cette définition implique que pour posséder un point d’inflexion en un point, la fonction doit posséder une tangente en ce même point (c’est-à-dire y être dérivable ou y posséder un point de non dérivabilité de type tangente verticale).
. $$ Attention : la réciproque est fausse ! \(f''(c) = 0\) n’implique pas l’existence d’un point d’inflexion en \(x=c\). Il faut pour cela que \(f''(c)\) change de signe en \(x=c\).
Dans le chapitre 3, on a utilisé les limites pour définir et calculer des dérivées. Nous allons voir qu’on peut aussi utiliser les dérivées pour calculer les limites.
Soient \(f\) et \(g\) deux fonctions dérivables en \(a\) telles que \(g'(x) \neq 0\) pour \(x\) proche de \(a\) (sauf peut-être en \(x=a\)). Supposons que \[ \lim_{x\rightarrow a} f(x) = 0 \quad \text{ et } \quad \lim_{x\rightarrow a} g(x) = 0 \] ou que \[ \lim_{x\rightarrow a} f(x) = \pm \infty \quad \text{ et } \quad \lim_{x\rightarrow a} g(x) = \pm \infty \] Alors \[ \boxed{ \quad \lim_{x\rightarrow a} \frac{f(x)}{g(x)} = \lim_{x\rightarrow a} \frac{f'(x)}{g'(x)} \quad} \] On remarque alors d’abord que la règle de l’Hospital dit que la limite qu’un quotient de fonction est égale à la limite du quotient des dérivées si et seulement si on a une forme indéterminée de type “0/0” ou de type “\(\infty/\infty\)” Si ce n’est pas le cas, la règle ne s’applique pas !
On voit aussi que la règle est aussi valable pour les limites à gauche ou à droite ainsi que pour les limites à l’infini.
Il est également possible d’utiliser indirectement la règle de l’Hospital pour les formes indéterminées de type “\(0 \cdot \infty\)” ou “\(\infty - \infty\)”. Dans ce cas, il suffit d’abord de transformer l’expression en une forme indéterminée “0/0” ou de type “\(\infty/\infty\)”, puis d’appliquer la règle de l’Hospital.
\[ \lim_{x\rightarrow 0^+} x \ln x = \lim_{x\rightarrow 0^+} \frac{\ln x}{x^{-1}} = \lim_{x\rightarrow 0^+} \frac{(\ln x)'}{(x^{-1})'} = \lim_{x\rightarrow 0^+} \frac{x^2}{x} \stackrel{x \neq 0}{=} \lim_{x\rightarrow 0^+} -x = 0 \]
On a jusqu’à présent appris à calculer la pente de la tangente au graphe d’une fonction. La variable \(y\) était alors explicitement exprimée en fonction de la variable \(x\). Il existe pourtant des courbes, qui ne sont pas des fonctions, pour lesquelles la relation entre les différentes variables s’exprime de manière implicite.
Soit l’équation \(x^2 + y^2 = 25\). Calculer \(\frac{dy}{dx}\).
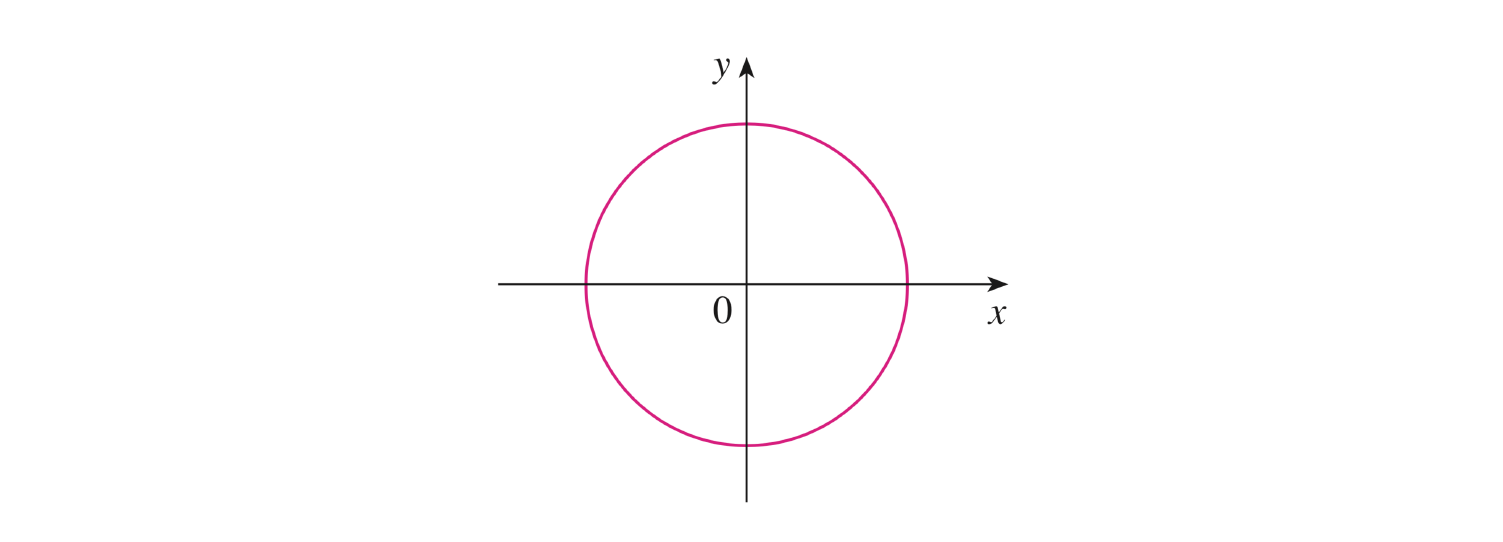
En dérivant l’équation \(x^2 + y^2 = 25\) par rapport à la variable \(x\) des côtés du signal égal, on obtient : \[ 2x + \frac{d}{dx} y^2 = 0 \] Pour dériver le terme \(y^2\) par rapport à la fonction \(x\), on considère \(y\) comme une fonction dépendant de \(x\), ce qui fait de \(y^2\) une composition de fonctions : \[ f(x) = y^2 = u(v(x)) \\\\ \begin{array}{ll} u(x) = x^2 & u'(x) = 2x \\ v(x) = y & v'(x) = y' \end{array} \] La règle de dérivation des fonctions composée donne alors : \[ (u(v(x)))' = u'(v(x)) \cdot v'(x) = 2y \cdot y' \] On obtient alors : \[ 2x + 2y \cdot y' = 0 \\ \Leftrightarrow \\ y' = \frac{dy}{dx} = - \frac{x}{y} \]
Le calcul des dérivées de certaines fonctions comportant des produits, des quotients et des puissances peut être souvent fortement simplifié en prenant des logarithmes. Cette méthode s’appelle la dérivation logarithmique.
Dériver logarithmiquement la fonction suivante : \[ f(x) = \frac{x^{\frac{3}{4}} \sqrt{x^2 +1} }{(3x + 2)^5} \] On applique la marche à suivre : $$ \[\begin{align} 1. \quad & y = \frac{x^{\frac{3}{4}} \sqrt{x^2 +1} }{(3x + 2)^5} \\\\ 2. \quad & \ln y = \ln{\left( \frac{x^{\frac{3}{4}} \sqrt{x^2 +1} }{(3x + 2)^5} \right)} \\\\ 3. \quad & \ln y = \ln (x^{\frac{3}{4}}) + \ln \left( (x^2 + 1)^{\frac{1}{2}} \right) - \ln \left((3x + 2)^5\right) \\ & \ln y = \frac{3}{4} \ln x + \frac{1}{2} \ln(x^2 + 1) - 5\ln(3x + 2) \\\\ 4. \quad & \frac{1}{y} \cdot y' = \frac{3}{4} \cdot \frac{1}{x} + \frac{1}{2} \cdot \frac{1}{x^2+1} \cdot 2x -5 \cdot \frac{1}{3x+2} \cdot 3 \\\\ 5. \quad & y' = y\left( \frac{3}{4x} + \frac{x}{x^2+1} - \frac{15}{3x+2} \right) \\\\ 6. \quad & f'(x) = \left( \frac{x^{\frac{3}{4}} \sqrt{x^2 +1} }{(3x + 2)^5} \right) \cdot \left ( \frac{3}{4x} + \frac{x}{x^2+1} - \frac{15}{3x+2}\right) \end{align}\] $$
Soit \(y\) une quantité dépendant d’une autre quantité \(x\), la dépendance étant de la forme \(y=f(x)\), où \(f\) est une fonction. Lorsque \(x\) varie de \(x_1\) à \(x_2\), sa variation est donnée par : \[ \Delta x = x_2-x_1 \] La variation de \(y\) qui en résulte est alors donnée par : \[ \Delta y = f(x_2) - f(x_1) \] On appelle taux de variation moyen de \(y\) par rapport à \(x\) sur l’intervalle \(\left[x_1,x_2\right]\) le quotient suivant : \[ \boxed{ \quad \frac{\Delta y}{\Delta x} = \frac{f(x_2)-f(x_1)}{x_2-x_1} \quad} \] Ce taux de variation moyen peut être interprété comme la pente de la sécante \(PQ\) au graphe de \(f\) passant par les points \(P(x_1, f(x_1))\) et \(Q(x_2,f(x_2))\). En faisant tendre \(x_2\) vers \(x_1\), on obtient le taux de variation instantané de \(f\) au point \(x = x_1\).

Le taux de variation instantané d’une fonction \(f\) par rapport à \(x\) en \(x_1\) est défini par : \[ \boxed{ \quad taux_{variation,inst} = \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{x_2 \rightarrow x_1} \frac{f(x_2)-f(x_1)}{x_2-x_1} = f'(x_1) \quad} \]
Il existe différentes interprétation pour le même concept de dérivée :
Il est parfois plus simple de déterminer un certain taux de variation, lui-même dépendant d’un autre. Par exemple, lorsqu’on gonfle un ballon, son volume et son rayon augmentent tout deux en fonction du temps. Ainsi, si on veut déterminer le taux de variation instantané du volume du ballon, il est en général plus facile de calculer le taux de variation du rayon dans un premier temps, puis d’en déduire ensuite celui du volume par calculs.
C’est le principe des taux de variations liés ; on calcule un certain taux de variation en fonction d’un autre, lié, supposé plus simple à déterminer.
Soit \(f\) une fonction dérivable en un point \(a\). La linéarisation de \(f\) centrée en \(a\) est la fonction affine \(L(x)\) dont le graphe est la tangente au graphe de \(f\) en \(a\). L’approximation linéaire de \(f\) centrée en \(a\) est l’approximation de \(f\) par sa linéarisation centrée en \(a\) : \[ \boxed{ \quad f(x) \cong L(x) \quad} \quad\text{ pour $x$ proche de $a$} \]
Soit la fonction \(f\) définie par : \[ f(x) = (1+x)^k \space , \quad k \in \R \] On cherche l’expression algébrique de la linéarisation centrée en \(0\) de la fonction \(f\).
On a : \[ f'(x) = k(1+x)^{k-1} \space , \quad f'(0) = k \] Comme de plus, \(f(0) = 1\), l’expression algébrique de la linéarisation est donnée par : \[ L(x) = kx + 1 \] L’approximation linéaire de \(f\) centrée en \(0\) est alors donnée par : \[ (1+x)^k \cong kx + 1 \space , \quad\text{pour $x$ proche de $0$} \]
Soit \(f:D \longmapsto \R\) une fonction et soit \(a \in D\). La variation absolue de \(f\) sur l’intervalle \(\left[ \space a \space ; \space a+\Delta x \right]\) est définie par : \[ \boxed{ \quad \Delta y = f(a + \Delta x) - f(a) \quad} \] La variation relative de \(f\) sur l’intervalle \(\left[ \space a \space ; \space a+\Delta x \right]\) est définie par : \[ \boxed{ \quad \frac{\Delta y}{y} = \frac{f(a+\Delta x)-f(a)}{f(a)} \quad} \] Si la fonction \(f\) est dérivable, on peut utiliser l’approximation linéaire de \(f\) centrée en \(a\) pour obtenir une approximation de la variation absolue \(\Delta y\). Sur la figure suivante, on peut approximer la fonction \(f\) sur l’intervalle \(\left[ \space a \space ; \space a+\Delta x \right]\) par : \[ \Delta y \cong f'(a) \cdot \Delta x \] Pour \(\Delta x\) proche de \(0\).
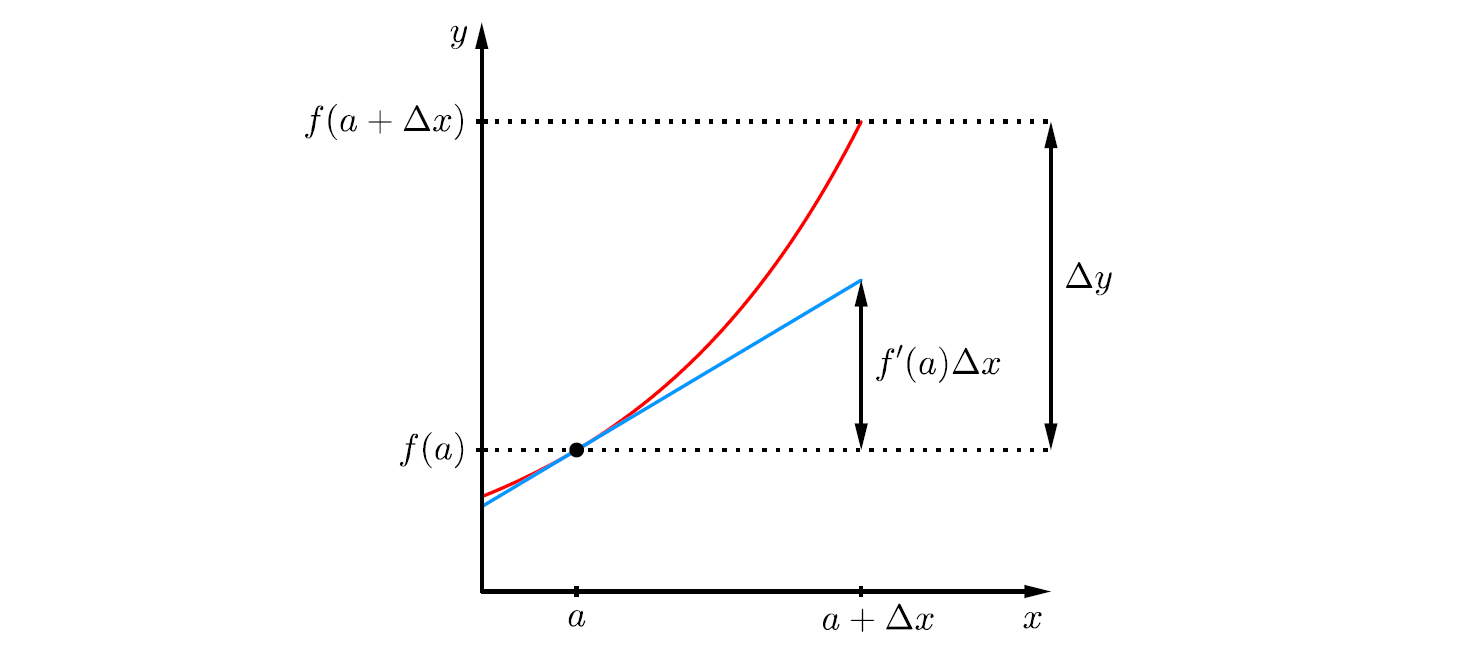
Supposons qu’on ait effectué une mesure \(x=a \pm \Delta x\). Alors l’incertitude absolue \(\Delta y\) induite sur \(y\) par la relation \(y= f(x)\) peut être approximée par : \[ \boxed{ \quad \Delta y \cong \abs{f'(a)} \cdot \Delta x \quad} \]
Soit \(f : D \longmapsto \R\) une fonction dérivable et soit \(a \in D\).
Si \(f=u + v\) est une somme de deux fonction \(u\) et \(v\), alors les variations absolues s’additionnent : \[ \boxed{ \quad \Delta y \cong \Delta u + \Delta v \quad} \]
Si \(f=u \cdot v\) est un produit de deux fonctions \(u\) et \(v\), alors les variations relatives s’additionnent : \[ \boxed{ \quad \frac{\Delta y}{y} \cong \frac{\Delta u}{u} + \frac{\Delta v}{v} \quad} \]
Soit \(f\) une fonction satisfaisant les trois hypothèses suivantes :
Alors il existe un nombre \(c \in ]a,b[\) tel que \(f'(c) = 0\).
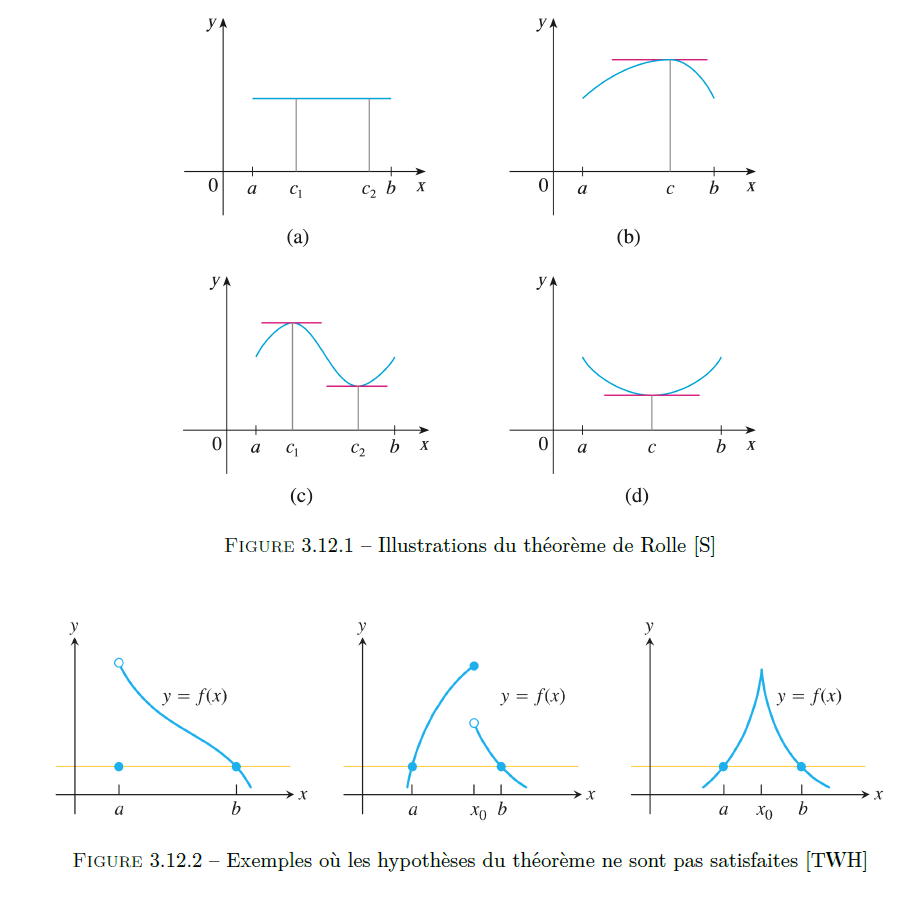
Soit \(f\) une fonction satisfaisant les deux hypothèses suivantes :
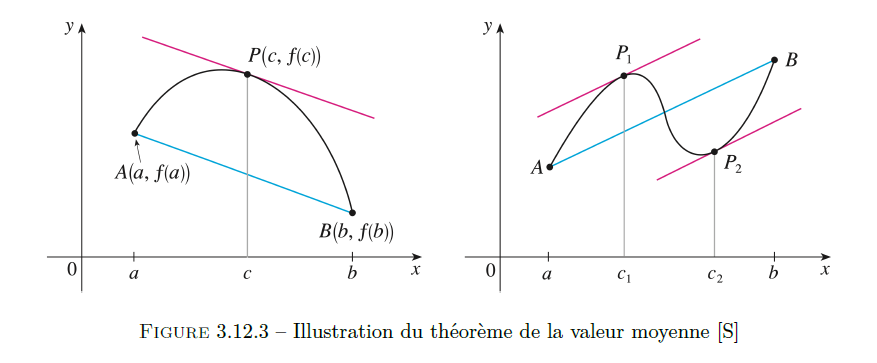
Alors il existe un nombre \(c \in ]a,b[\) tel que \[
f'(c) = \frac{f(b)-f(a)}{b-a}
\] 
Exported with pandoc 2.9.2.1 on Thu May 19 2022 at 15:46:25 CEST. @ylked
All informations are given without warranty. All rights reserved ©