Chapitre 2 - Limites

2.1 Définition des limites

2.1.1 Définition intuitive des limites

Définition 2.1.3

Soit $f$$f$ une fonction. On dit que "la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ est égale à $L$$L$" si les valeurs de $f(x)$$f(x)$ s'approchent de $L$$L$ lorsque $x$$x$ s'approche de $a$$a$, sans être égal à $a$$a$. On écrit alors :

Ce qui se passe en $x=a$$x=a$ ne joue aucun rôle dans la valeur de $L$$L$. $f$$f$ n'a même pas besoin d'être définie en $a$$a$. Tout ce qui compte est la valeur $L$$L$ vers laquelle $f$$f$ tend quand $x$$x$ tend vers $a$$a$.

Exemple 2.1.4

Soit $f$$f$ la fonction définie par :

dont le graphe est représenté ci-dessous :

Lorsque $t$$t$ tend vers 0 par la gauche, $f(t)$$f(t)$ tend vers 0 mais lorsque $t$$t$ tend vers 0 par la droite, $f(t)$$f(t)$ tend vers 1. Ainsi

En effet, il n'existe pas un nombre unique $L$$L$ vers lequel $f(t)$$f(t)$ tend quand $t$$t$ tend vers 0.

2.1.2 Limites à gauche et à droite

Définition 2.1.7

Soit $f$$f$ une fonction. La limite à gauche de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ est la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ avec $x<a$$x<a$. On l'écrit :

De manière analogue, on définit : la limite à gauche de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ est la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ avec $x<a$$x<a$. On l'écrit :

Théorème 2.1.9

Soit $f$$f$ une fonction. Alors :

2.1.3 Limites infinies

Définition 2.1.10

Soit $f$$f$ une fonction. On dit que "la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ est égale à l'infini" si les valeurs de $f(x)$$f(x)$ deviennent arbitrairement grandes lorsque $x$$x$ s'approche de $a$$a$, sans être égal à $a$$a$. Dans ce cas, on écrit :

De manière analogue, on dit que "la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers $a$$a$ est égale à moins l'infini" si les valeurs de $f(x)$$f(x)$ deviennent arbitrairement négativement grandes lorsque $x$$x$ s'approche de $a$$a$, sans être égal à $a$$a$​. Dans ce cas, on écrit

Définition 2.1.11

Soit $f$$f$ une fonction. Si l'une des six conditions ci-dessous est vérifiée :

on dit alors que la droite verticale d'équation $x=a$$x=a$ est une asymptote verticale de $f$$f$.

2.1.5 Limites à l'infini

Définition 2.1.12

Soit $f$$f$ une fonction. On dit que "la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers l'infini est égale à $L$$L$" si les valeurs de $f(x)$$f(x)$ s'approchent de $L$$L$ lorsque les valeurs de $x$$x$ deviennent arbitrairement grandes. Dans ce cas, on écrit :

De manière analogue, on dit que "la limite de $f(x)$$f(x)$ lorsque $x$$x$ tend vers moins l'infini est égale à $L$$L$" si les valeurs de $f(x)$$f(x)$ s'approchent de $L$$L$ lorsque les valeurs de $x$$x$ deviennent arbitrairement négativement grandes. Dans ce cas, on écrit :

Définition 2.1.13

Soit $f$$f$ une fonction. Si l'une des deux conditions ci-dessous est vérifiée :

On dit alors que la droite horizontale d'équation $y=L$$y=L$ est une asymptote horizontale de $f$$f$.

2.2 Calcul de limites polynomiales et rationnelles

2.2.1 Règles de calcul

Théorème 2.2.1

Supposons que les limites suivantes existent :

Alors :

Théorème 2.2.2

On a

Théorème 2.2.5

Soit une fonction polynomiale ou rationnelle et soit $a\in D_f$$a \in D_f$ un point du domaine de définition de $f$$f$. Alors :

Si $f$$f$ est une fonction polynomiale ou rationnelle, il est alors très simple de calculer la limite en un point $a$$a$ du domaine de définition : il suffit de remplacer $x$$x$ par $a$$a$.

2.2.2 Formes indéterminées de type "0/0"

Définition 2.2.7

Une limite

est une forme indéterminée de type "0/0" si

Pour déterminer la valeur d'une limite de forme indéterminée de type "0/0", il faut simplifier le numérateur et le dénominateur par le facteur $(x-a)$$(x-a)$ !

2.2.3 Récapitulation

Pour calculer la valeur d'une limite de la forme :

Où $f$$f$ est une fonction polynomiale et rationnelle, on peut appliquer la méthode suivante :

1. La valeur appartient au domaine de définition

Si $a\in D_f$$a \in D_f$, alors

2. Dénominateur nul et numérateur constant non-nul

Si la limite est de la forme

Elle peut alors soit tendre vers $\pm \mathrm{\infty }$$\pm \infty$, soit ne pas exister.

Si elle tend vers $\pm \mathrm{\infty }$$\pm\infty$, il faut alors déterminer le signe de l'infini.

3. Forme indéterminée "0/0"

Si la limite est de la forme

Il faut alors simplifier le numérateur et le dénominateur par le facteur $(x-a)$$(x-a)$ avant de calculer la limite (on devrait alors pouvoir remplacer $x$$x$ par $a$$a$).

2.3 Continuité

2.3.1 Définition

Définition 2.3.1

Une fonction $f$$f$ est dite continue en $a$$a$ si

Si $f$$f$ n'est pas continue en $a$$a$, on dit qu'elle est discontinue en $a$$a$.

Cette définition dit qu'une fonction est continue en $a$$a$ si on peut calculer $\underset{x\to a}{lim}f(x)$$\lim_{x\rightarrow a}f(x)$ en remplaçant $x$$x$ par $a$$a$ dans l'expression algébrique de $f$$f$.

De manière graphique, cela signifie que quand $x$$x$ tend vers $a$$a$, les valeurs de $f(x)$$f(x)$ tendent vers $f(a)$$f(a)$.

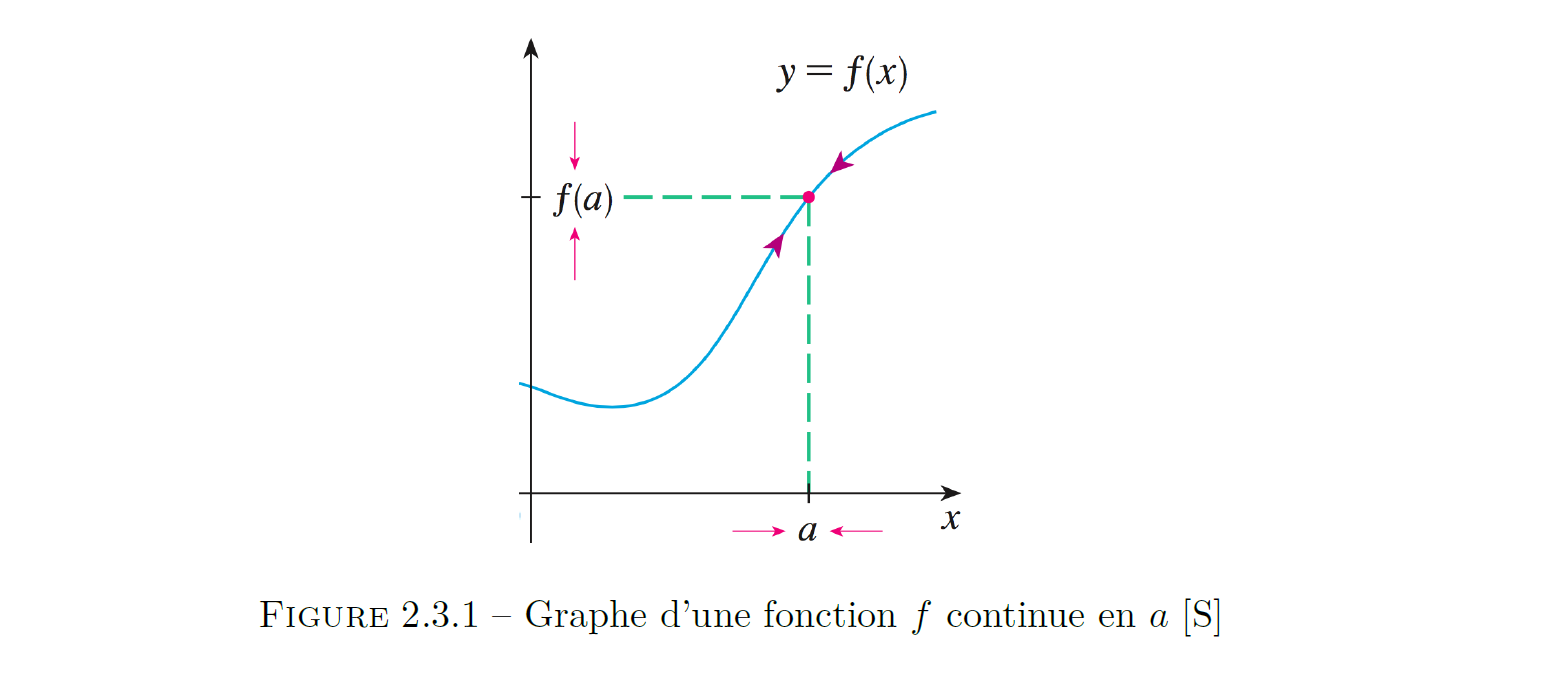
La définition implique alors :

Si une seule de ces conditions n'est pas satisfaite en $a$$a$, alors $f$$f$ est discontinue en $a$$a$.

Ce qui se passe en $x=a$$x=a$ est donc crucial pour la continuité de $f$$f$ en $a$$a$.

Définition 2.3.2

Une fonction $f$$f$ possède en $x=a$$x=a$ :

1. Une discontinuité de type trou si

   $$\underset{x\to a}{lim}f(x)\in \mathbb{R}\text{ mais }f(a)\text{ n’existe pas}$$

2. Une discontinuité de type trou-saut si

   $$\underset{x\to a}{lim}f(x)\in \mathbb{R}\text{ mais }\underset{x\to a}{lim}f(x)\ne f(a)$$

3. Une discontinuité de type saut si

   $$\underset{x\to a}{lim}f(x)\text{ n’existe pas mais }\underset{x\to a^{-}}{lim}f(x)\in \mathbb{R}\text{ et }\underset{x\to a^{+}}{lim}f(x)\in \mathbb{R}$$

4. Une discontinuité de type infini si

   $$\underset{x\to a}{lim}f(x)=\pm \mathrm{\infty }\text{ ou }\underset{x\to a^{-}}{lim}f(x)=\pm \mathrm{\infty }\text{ ou }\underset{x\to a^{+}}{lim}f(x)=\pm \mathrm{\infty }$$

Définition 2.3.5

Une fonction est dite continue à gauche en $a$$a$ si

et continue à droite en $a$$a$ si

Définition 2.3.7

Une fonction est dite continue sur un ensemble $A$$A$ si elle est continue $\mathrm{\forall }a\in A$$\forall a \in A$.

Liste de fonctions continues

Théorème 2.3.9

Les fonctions suivantes sont continues en tout point de leurs domaines de définition :

1. Les fonctions puissances : $x^n$$x^n$
2. Les fonctions racines : $\sqrt[n]{x}$$\sqrt[n]{x}$
3. Les fonctions polynomiales : $a_n{x}^n+...+a_{1}x+a_0$$a_nx^n+...+a_1x + a_0$
4. Les fonctions rationnelles : $\frac{p(x)}{q(x)}$$\frac{p(x)}{q(x)}$ où $p(x)$$p(x)$ et $q(x)$$q(x)$ sont des polynômes
5. La fonction valeur absolue : $\left|x\right|$$\abs{x}$
6. Les fonctions exponentielles : $a^x$$a^x$
7. Les fonctions logarithmiques : $lo{g}_{a}x$$log_a x$
8. Les fonctions trigonométriques : $\sin x$$\sin x$, $\cos x$$\cos x$, $\tan x$$\tan x$
9. Les fonctions trigonométriques inverses : $\arcsin x$$\arcsin x$, $\arccos x$$\arccos x$, $\arctan x$$\arctan x$

Théorème 2.3.10

Soient $f$$f$ et $g$$g$ deux fonctions continues sur leurs domaines de définition. Alors les fonctions suivantes sont également continues sur leurs domaines de définition.

1. $f+g$$f+g$
2. $f-g$$f-g$
3. $f\cdot g$$f \cdot g$
4. $f\cdot g^{-1}$$f \cdot g^{-1}$
5. $f\circ g$$f\circ g$

2.3.3 Utilisation de la continuité dans le calcul de limites

Théorème 2.3.14

Soit $f$$f$ une fonction continue en $b$$b$ et $g$$g$ une fonction telle que

Alors

Exemple 2.3.15

Calculer

La fonction $\arctan$$\arctan$ est continue en n'importe quel point de son domaine de définition $D=\mathbb{R}$$D=\R$

Par le théorème 2.3.14, on a

2.4 Calcul des limites à l'infini

2.4.1 Arithmétique de l'infini

Il est important de connaitre par cœur les quatre formes indéterminées :

2.4.2 Limites à l'infini des puissances

Théorème 2.4.1

Soit

une fonction puissance. Alors :

1. Si $n$$n$ est impair, $\underset{x\to -\mathrm{\infty }}{lim}f(x)=-\mathrm{\infty }$$\lim_{x\rightarrow -\infty}f(x)=-\infty$ et $\underset{x\to +\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }$$\lim_{x\rightarrow +\infty}f(x)=+\infty$
2. Si $n$$n$ est pair, $\underset{x\to -\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }$$\lim_{x\rightarrow -\infty}f(x)=+\infty$ et $\underset{x\to +\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }$$\lim_{x\rightarrow +\infty}f(x)=+\infty$

2.4.3 Limites à l'infini des polynômes

Soit :

un polynôme de degré $n$$n$. Alors

Ce théorème affirme que le comportement à l'infini d'un polynôme est le même que celui de son terme dominant $a_n{x}^n$$a_nx^n$.

2.4.4 Limites à l'infini des fonctions rationnelles

Théorème 2.4.5

Soit

une fonction rationnelle. Alors

Ce théorème affirme que le comportement à l'infini d'une fonction rationnelle est le même que celui du quotient des termes dominants $a_m{x}^m$$a_mx^m$ et $b_n{x}^n$$b_nx^n$ du numérateur et du dénominateur.

Théorème 2.4.7

Soit

une fonction rationnelle. Alors

2.4.5 Limites à l'infini d'autres types de fonctions

Exemple 2.4.9