Chapitre 1 - Fonctions
Chapitre 1 - FonctionsFonctions et graphesDéfinition d'une fonctionDéfinition 1.1.1 : Graphe d'une fonctionDéfinition 1.1.3 : Théorème 1.1.6Domaine de définition et ensemble imageDéfinition 1.1.7Définition 1.1.11Opérations sur les fonctionsTranslations, dilatations, compressions et symétriesThéorème 1.2.1Théorème 1.2.3Parité des fonctionsDéfinition 1.2.5Définition 1.2.6Composition de fonctionsDéfinition 1.2.9Fonctions quadratiquesDéfinitionDéfinition 1.3.1Formes développéeThéorème 1.3.2Théorème 1.3.3Forme factoriséeThéorème 1.3.51.
Fonctions et graphes
Définition d'une fonction
Définition 1.1.1 :
une fonction
D est l'ensemble de départ de la fonction
Graphe d'une fonction
Définition 1.1.3 :
Soit
Le graphe de la fonction
Théorème 1.1.6
Une courbe dans le plan est une fonction ssi aucune droite verticale ne coupe la courbe plus d'une fois.
Domaine de définition et ensemble image
Définition 1.1.7
Si non précisé, le domaine de définition d'une fonction
Définition 1.1.11
L'ensemble image d'une fonction
Opérations sur les fonctions
Translations, dilatations, compressions et symétries
Théorème 1.2.1
Soit
Théorème 1.2.3
Soit
Parité des fonctions
Définition 1.2.5
Soit
On dit que
Définition 1.2.6
Soit
On dit que
Composition de fonctions
Définition 1.2.9
Soient
La fonction composée de
Le domaine de définition de la composition vaut alors :
Fonctions quadratiques
Définition
Définition 1.3.1
Une fonction
Dans la pratique on écrit l'expression sous trois formes différentes :
- développée :
- factorisée :
- canonique :
On voit que le coefficient
→ Si
→ Si
Formes développée
Théorème 1.3.2
Soit
Soit
Théorème 1.3.3
Soit
Le sommet du graphe de
passe inévitablement par ce point. Cela implique que la coordonnée du sommet vaut
Forme factorisée
La forme dite factorisée sous la forme
Théorème 1.3.5
Soit
1.
On peut alors factoriser
2.
On peut factoriser la fonction
3.
On ne peut alors pas factoriser
Forme canonique
La forme canonique permet de facilement dessiner le graphe de la fonction.
En effet, on constate qu'on obtient la parabole
- Une translation horizontale de
- Une homothétie verticale d'un facteur
- Une translation verticale de
Le sommet de la parabole se trouve alors en
Fonctions polynomiales
Définition
Définition 1.4.1
Un polynôme de degré
Où
Les nombres
Racines et factorisation de polynômes
Théorème 1.4.3
Soit
Si le facteur
Théorème 1.4.5
Si
procédure pour factoriser
par exemple
on trouve une racine simple
on divise
On détermine le quotient en sachant que :
Pour notre exemple :
Théorème 1.4.7
Un polynôme
- polynômes de degré 1 de type
- polynômes de degré 2 de type
Equations polynomiales
Pour résoudre une équation polynomiale, il suffit de la réécrire sous la forme
exemple
Inéquations polynomiales
Etapes pour la résolution d'inéquations polynomiales :
- Mettre tous les termes du même côté
- Factoriser au maximum
- Faire une étude de signe
- En déduire la solution
Fonction rationnelles
Définition
Définition
Une fonction rationnelles est une fonction de la forme :
Où
La fonction rationnelles la plus simple est la fonction
Son domaine de définition est
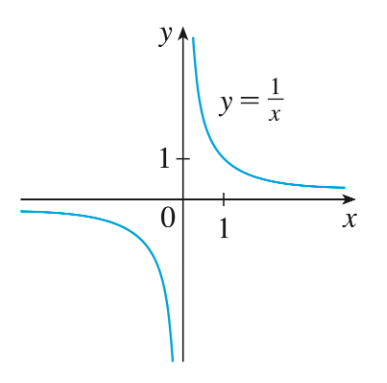
En utilisant les transformations géométriques, il est possible, à partir de la fonction
Equations rationnelles
L'idée générale est de se ramener à une équation polynomiale en multipliant l'équation par les dénominateurs.
Il faut en revanche faire attention aux conditions d'existences, càd exclure les divisions par zéro ou les racines de nombres négatifs de l'ensemble solution.
Marche à suivre pour résoudre une équation rationnelle
- Déterminer les conditions d'existence
- Se ramener à une équation polynomiale
- Résoudre l'équation polynomiale
- En déduire l'ensemble solution
Ne pas oublier de vérifier que les solutions satisfont les conditions d'existence!
Inéquations rationnelles
L'idée générale est de mettre tous les termes du même côté de l'inégalité, puis de faire une étude de signe.
Il ne faut pas se ramener à une inéquation polynomiale en multipliant l'inégalité par les dénominateurs
En effet, on sait que lorsque l'on multiplie ou divise par une valeur négative, on doit changer le signe de l'inégalité. Or, on n'a aucun moyen de connaitre le signe du dénominateur avant d'avoir entièrement résolu l'inéquation (sauf cas spécifiques).
Marche à suivre pour résoudre une inéquation rationnelle
- Déterminer les conditions d'existence
- Mettre tous les termes du même côté de l'inégalité
- Réécrire le membre non-nul comme une seule fonction rationnelle
- Factoriser le numérateur et le dénominateur jusqu'à obtenir des polynômes premiers entre eux.
- Effectuer une étude de signe
- Déduire l'ensemble solution
Fonctions exponentielles
Propriété des puissances
Soit une fonction exponentielle du type
Si
Si
Si
Si
Fonctions exponentielles
Définition 1.6.1
Soit
Dans la figure suivante, on a représenté les graphes de fonctions exponentielles
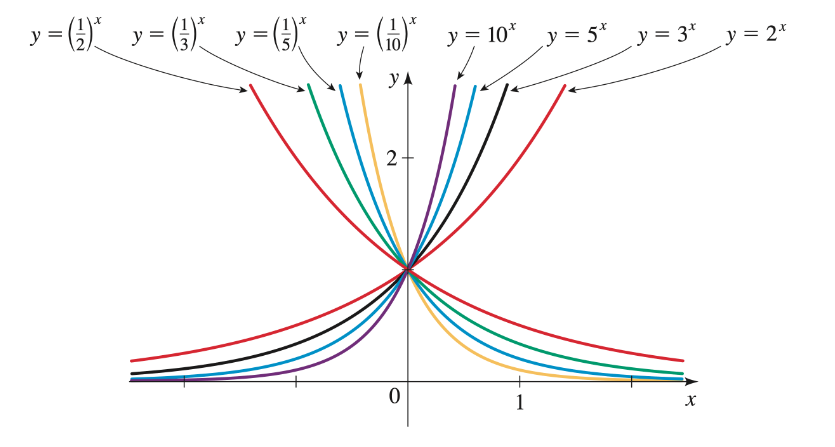
On peut alors distinguer essentiellement trios types de fonctions exponentielles en fonction de la valeur de la base
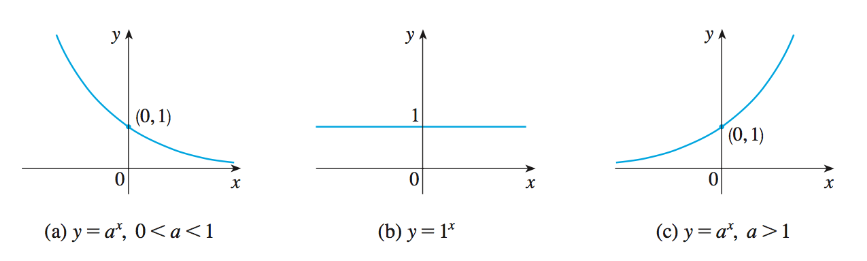
Fonction exponentielle naturelle
De toutes les bases possibles, il y en a une qui convient particulièrement au calcul différentiel : il s'agit du nombre d'Euler
En effet, la dérivée fonction
On appelle alors la fonction
Règles de calcul des puissances
Théorème 1.6.4
Soient
Equations et inéquations exponentielles (partie 1)
Contrairement aux équations et inéquations polynomiales ou rationnelles, il n'existe pas de marche à suivre systématique pour résoudre une équation ou inéquation exponentielle.
En revanche, il peut être utile d'exploiter le fait que :
Fonctions inverses
Inversibilité
Définition
Une fonction
Théorème
Une fonction
Fonctions inverses
Définition
Soit
Théorème
Soit
Graphe d'une fonction inverse
Par la définition, on a
Ainsi, un point
Or les points
Ceci explique le théorème suivant :
Théorème
Soit
Détermination de l'expression algébrique de
Si
- Ecrire
- Résoudre l'équation en
- Permuter
Fonctions logarithmiques
Définition
On voit que la fonction exponentielle
Définition 1.8.1
Soit
Théorème 1.8.2
On a :
Ainsi, lorsque
Théorème 1.8.4
On a
Logarithme naturel
On a vu au chapitre que l'exponentielle de base de nombre d'Euler
On a aussi :
et
Dans le cas particulier où
Règles de calcul des logarithmes
Théorème 1.8.5
Soit
Equations et inéquations logarithmiques
Comme pour les équations exponentielles, il n'existe pas de marche à suivre précise pour résoudre des équations logarithmiques.
En revanche, il peut être utile d'exploiter le fait que
Car les fonctions
Il faut par contre faire attention aux conditions d'existence :
Théorème 1.8.8
- Si
- Si
Prendre un logarithme de base
dans une inéquation change le sens de l'inégalité
Equations et inéquations exponentielles (partie 2)
Grâce aux logarithmes, on a tous les outils pour résoudre les équation (ou inéquation) exponentielles quelconques sous la forme
Exemple
Résoudre l'équation
Solution :
Ainsi l'ensemble solution vaut :
Fonctions trigonométriques
Mesure des angles en radians
Définition 1.9.1
La mesure d'un angle
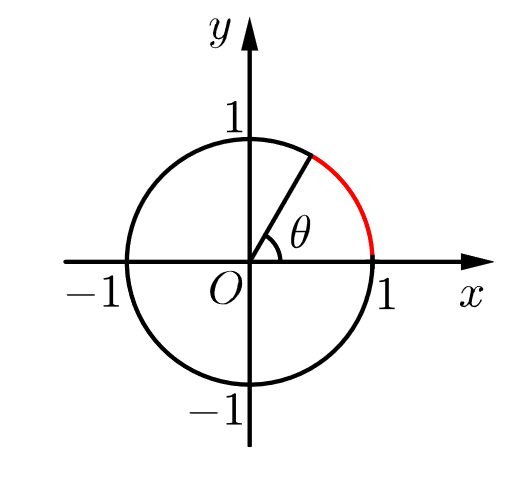
Par convention, les angles sont positifs quand on les mesure dans le sens anti-horaire et négatif dans le sens horaire.
Définition des fonctions trigonométriques
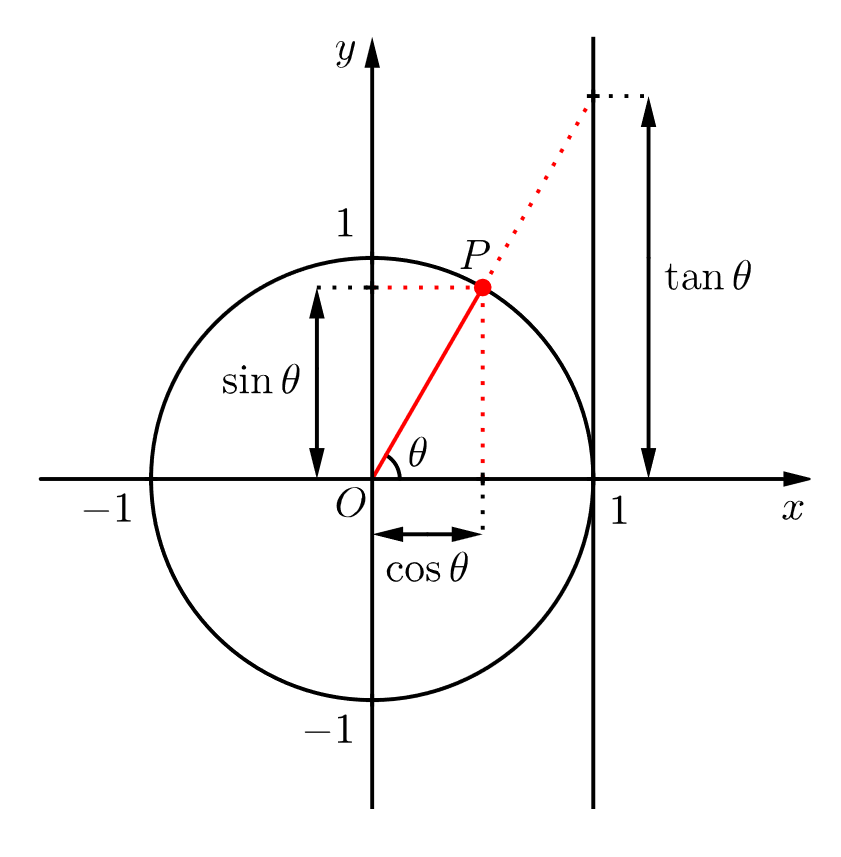
Définition 1.9.2
Soit
- On appelle cosinus de
- On appelle sinus l'ordonnée de
- On appelle tangente de
Théorème 1.9.3
Dans le tableau suivant sont représentées les valeurs exactes des fonctions trigonométriques pour quelques valeurs d'angle.

Théorème 1.9.4
→ Ces identités sont à connaitre par cœur!
Graphes des fonctions trigonométriques
En analyse, dans les fonctions trigonométriques, les angles se mesurent toujours en radians.
Les fonctions
Le domaine de définition des fonctions
L'ensemble image des fonctions
Graphe de la fonction
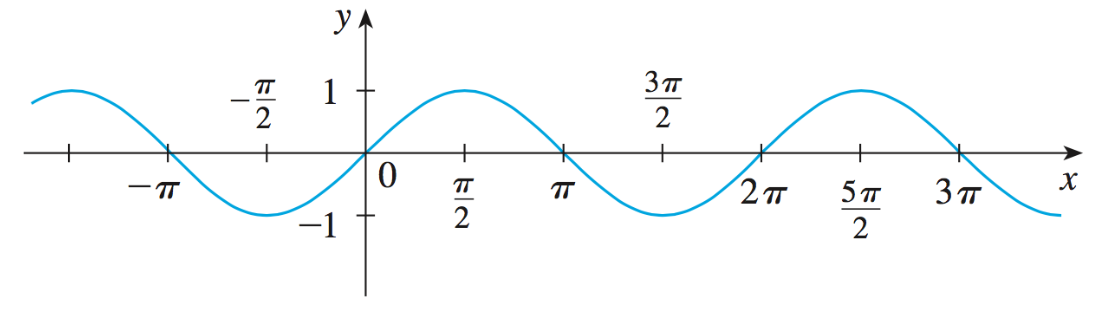
Graphe de la fonction
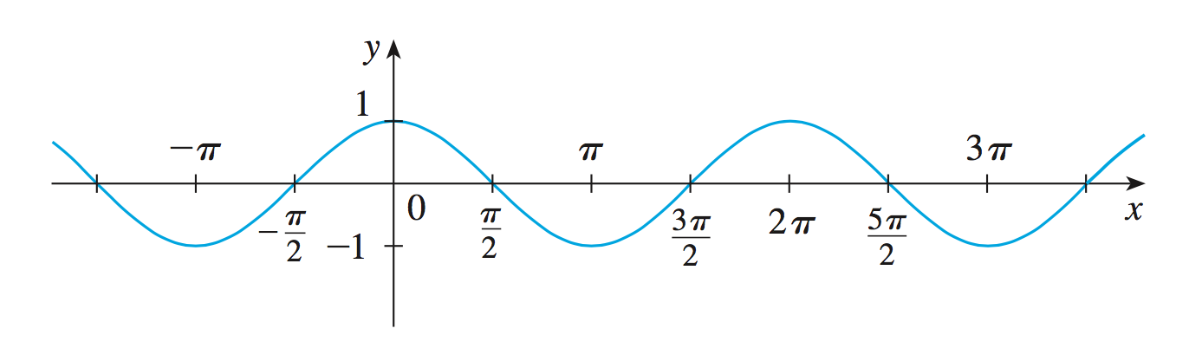
Le domaine de définition de la fonction
L'ensemble image de la fonction
Graphe de la fonction
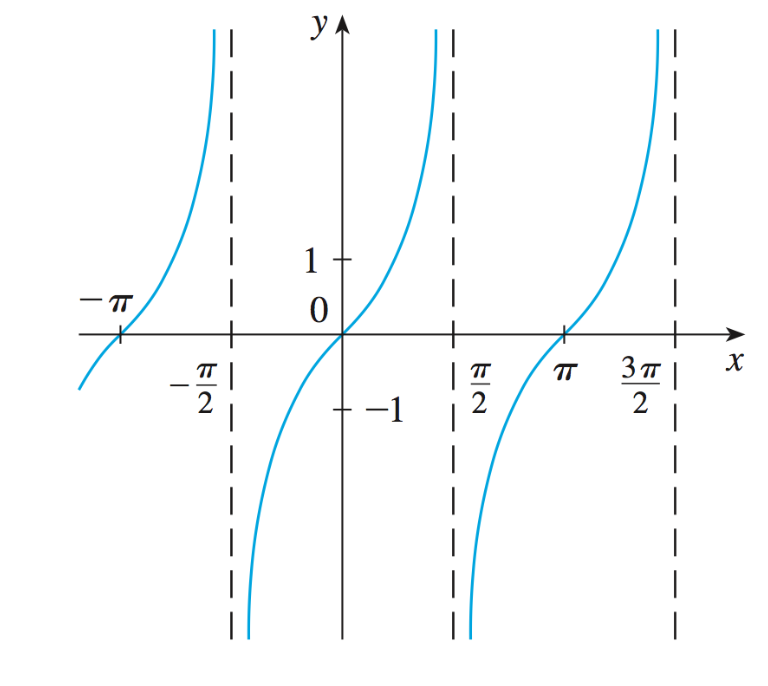
Remarque : Les fonctions sinus et tangentes sont impaires tandis que la fonction cosinus est paire.
Fonctions trigonométriques inverses
Les fonctions trigonométriques telles quelles ne sont pas injectives/inversibles. (Il existe une infinité de même valeur de cos/sin/tan pour un même angle
Définition 1.9.8
La fonction arcsinus, notée
A un nombre réel
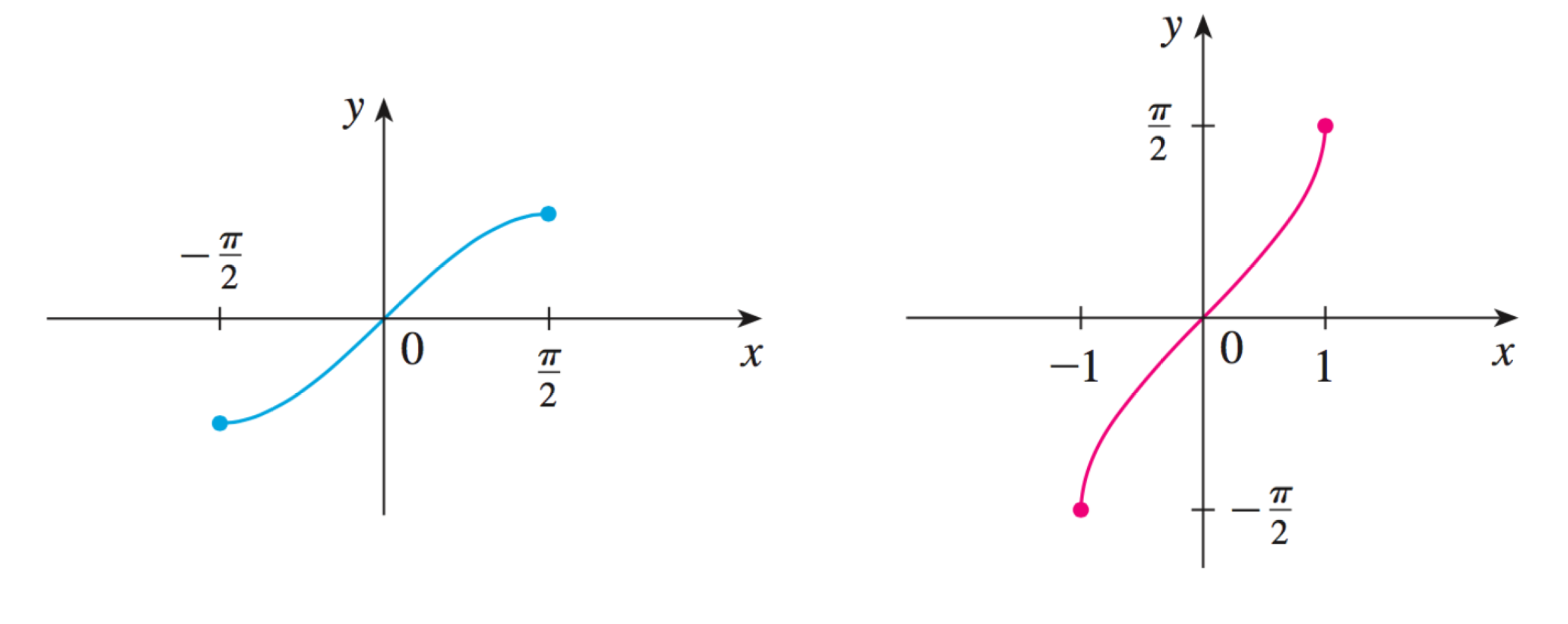
Le domaine de définition de la fonction
L'ensemble image de la fonction
Théorème 1.9.9
Les fonctions
Définition 1.9.10
La fonction arccosinus, notée
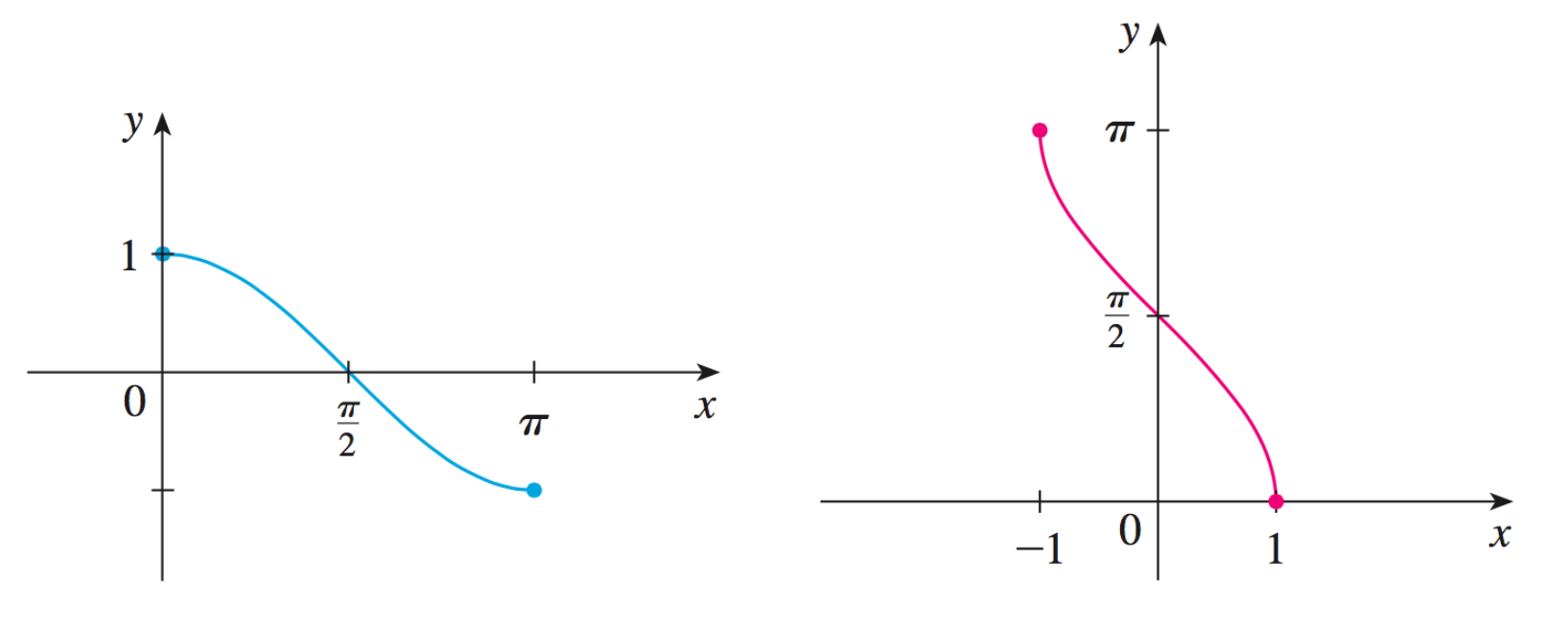
Le domaine de définition de la fonction
L'ensemble image de la fonction
Définition 1.9.11
La fonction arctangente, notée
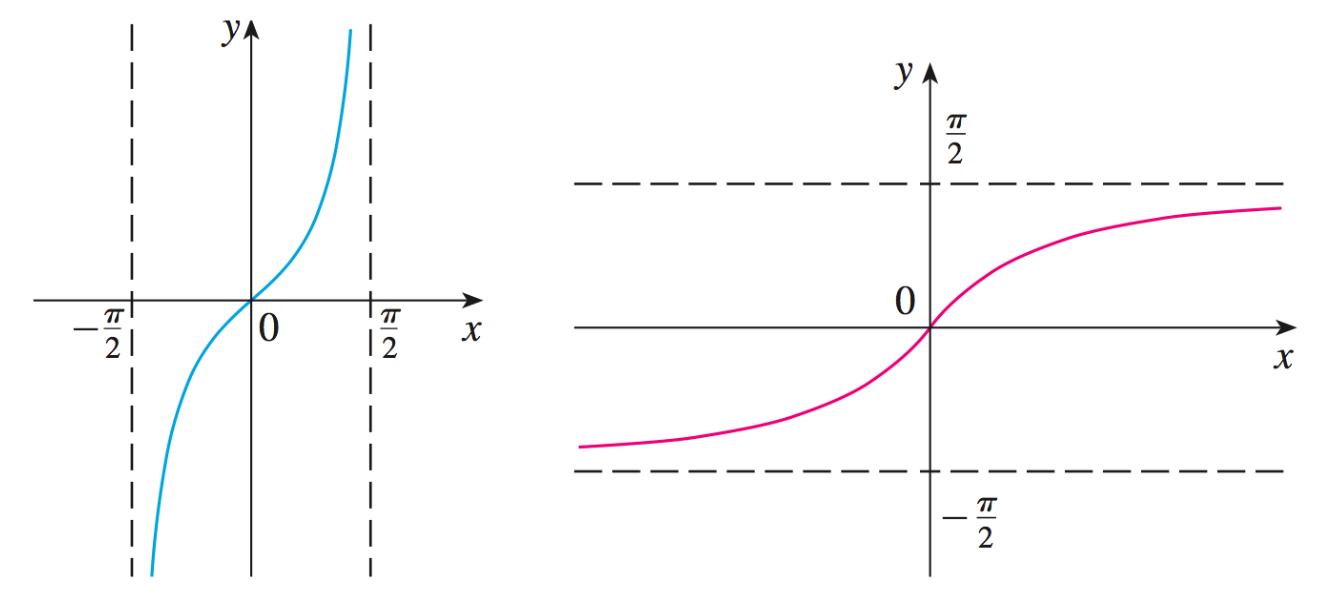
Le domaine de définition de la fonction
L'ensemble image de la fonction
Equations et inéquations trigonométriques
Les seules équations trigonométriques que l'on sait vraiment résoudre sont les équations de la forme
Il faut toujours faire attention aux conditions d'existence !
Fonctions définies par morceaux
On appelle les fonctions définies par morceaux, les fonctions dont l'expression algébrique diffère selon la partie du domaine de définition considéré.
Exemples
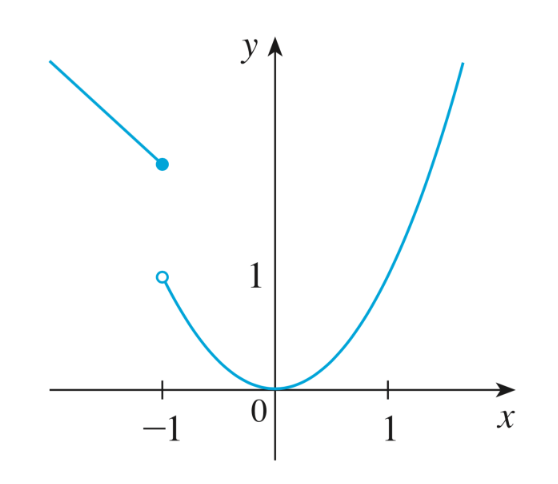
Exemple 1.10.1
Soit la fonction
Cette notation signifie que pour
Valeur absolue
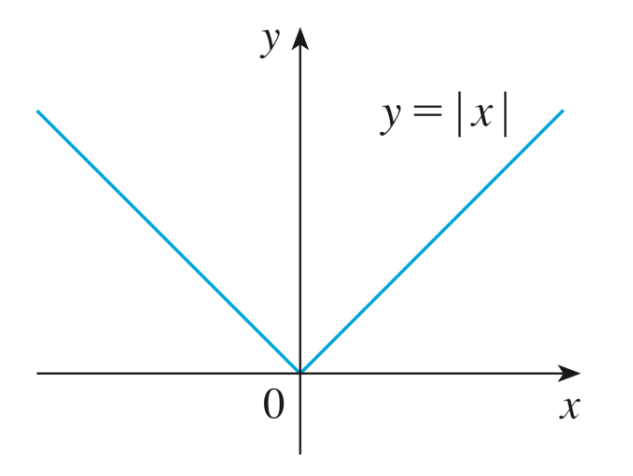
Définition 1.10.4
La fonction valeur absolue, notée
Si
Théorème 1.10.7
Soient
Théorème 1.10.8
Soit
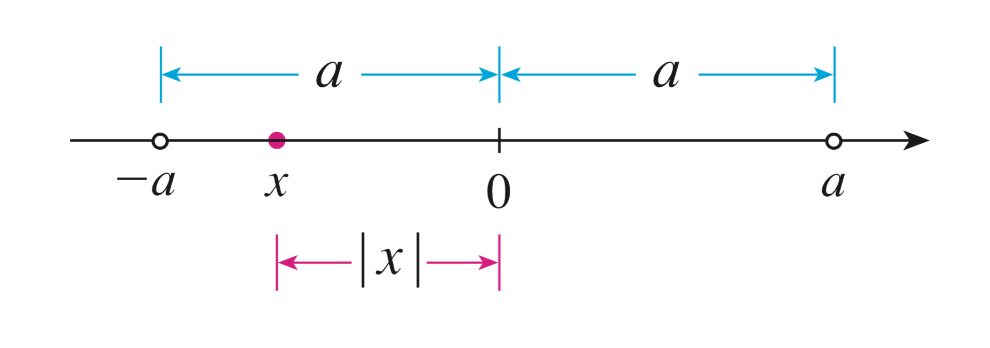
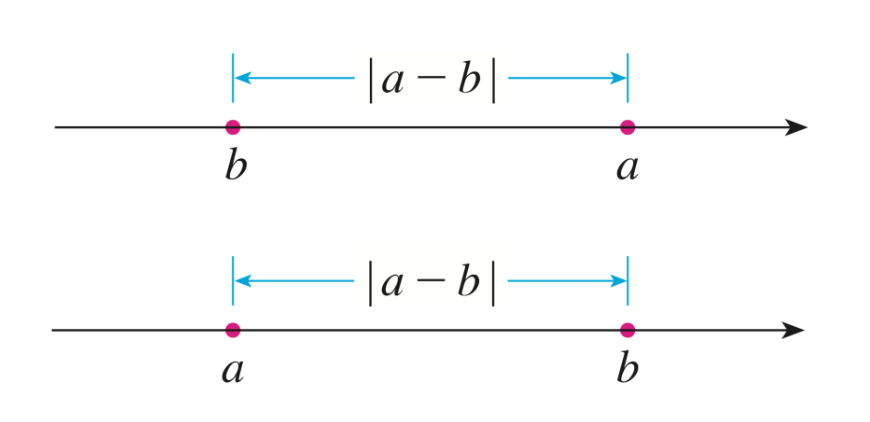
Théorème 1.10.9
Soient
Exemple 1.10.11
Résoudre l'inéquation
On se base sur le théorème 1.10.8 :
On a alors :