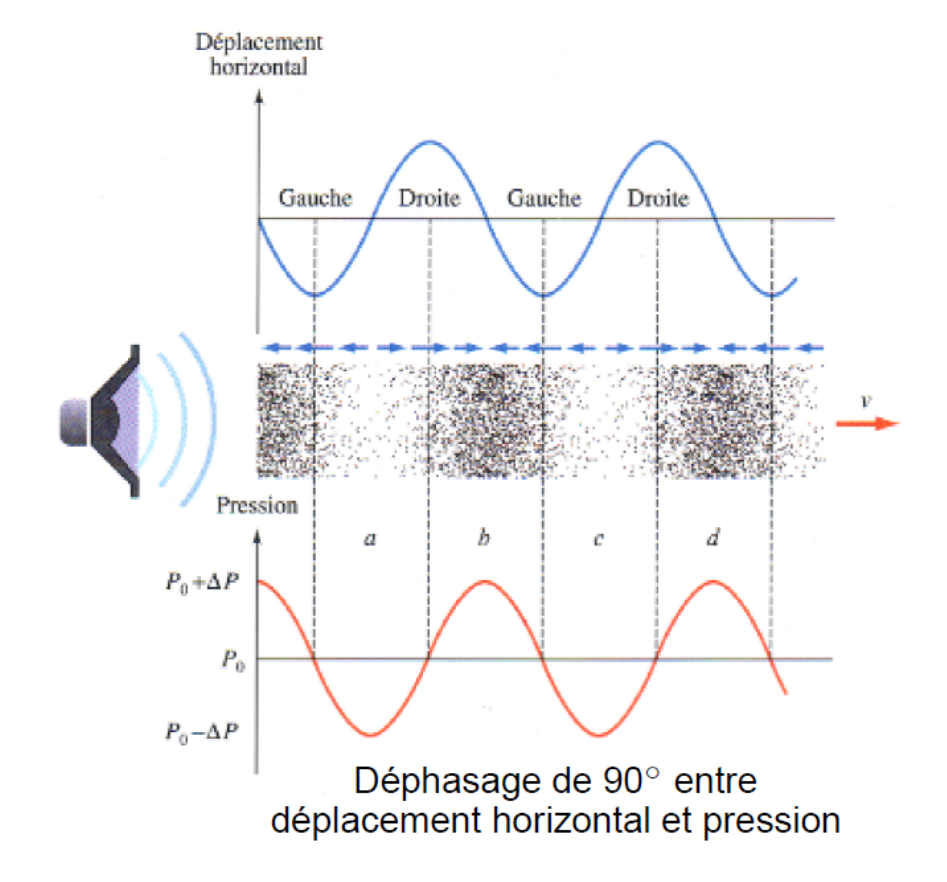
On appelle onde sonore ou son, toute onde mécanique longitudinale, indépendamment du type de milieu matériel dans lequel elle se propage.
C’est donc une différence de pression qui va se propager.
Sans milieu matériel, elle ne peut alors pas se déplacer !
A l’équilibre, la pression et la densité de l’air sont uniformes.
Lors du passage d’une onde, il y a une fluctuation de la densité et donc de la pression de l’air. La variation de la pression vaut : \(\Delta P_{max} \cong 1 \space Pa\)
La vitesse du son \(v_{son}\) ne dépend pas de la pression mais de la température :
\[ v_{son} \cong 20 \sqrt{\theta} \quad ms^{-1} \]
Où \(\theta\) est la température de l’air en Kelvin \([K]\)

Les ondes stationnaires peuvent être produites dans une colonne d’air, p.ex dans un tuyau.
On en distingue deux types :
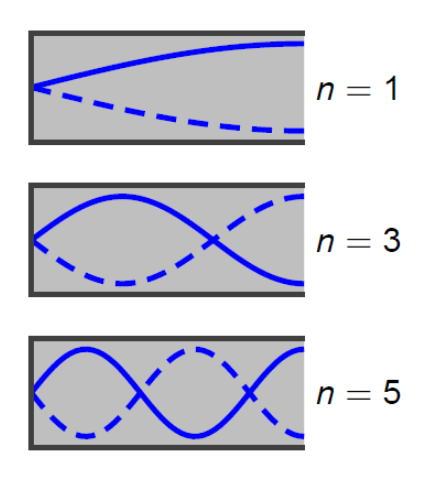
Caractéristiques des ondes aux extrémités du tuyau fermé :
La longueur d’onde et la fréquence des ondes stationnaires dans un tuyau fermé de longueur \(L\) sont alors :
\[ \boxed{ \lambda _n ={4L\over n} } \]
\[ \boxed{ f_n = {n\cdot v_{son}\over 4L}} \]
Avec \(n \geq 1\) impair.
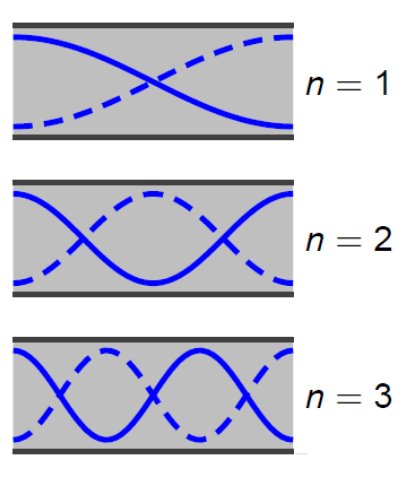
Il y a à chacune des deux extrémités ouvertes un ventre de déplacement et un noeud de pression.
La longueur d’onde et la fréquence des ondes stationnaires dans un tuyau ouvert de longueur \(L\) sont alors données par :
\[ \boxed{\lambda_n = {2L \over n}} \]
\[ \boxed{f_n = {n \cdot v_{son} \over 2L}} \]
Avec \(n\in \mathbb{N}^*\)
On appelle battement, la superposition de la partie temporelle de deux ondes sonores progressives de fréquences \(f_1\) et \(f_2\) proches.
\[ y_1(t) = A\sin(2\pi f_1 t) \quad \text{ et } \quad y_2(t) = A\sin(2\pi f_2 t) \]
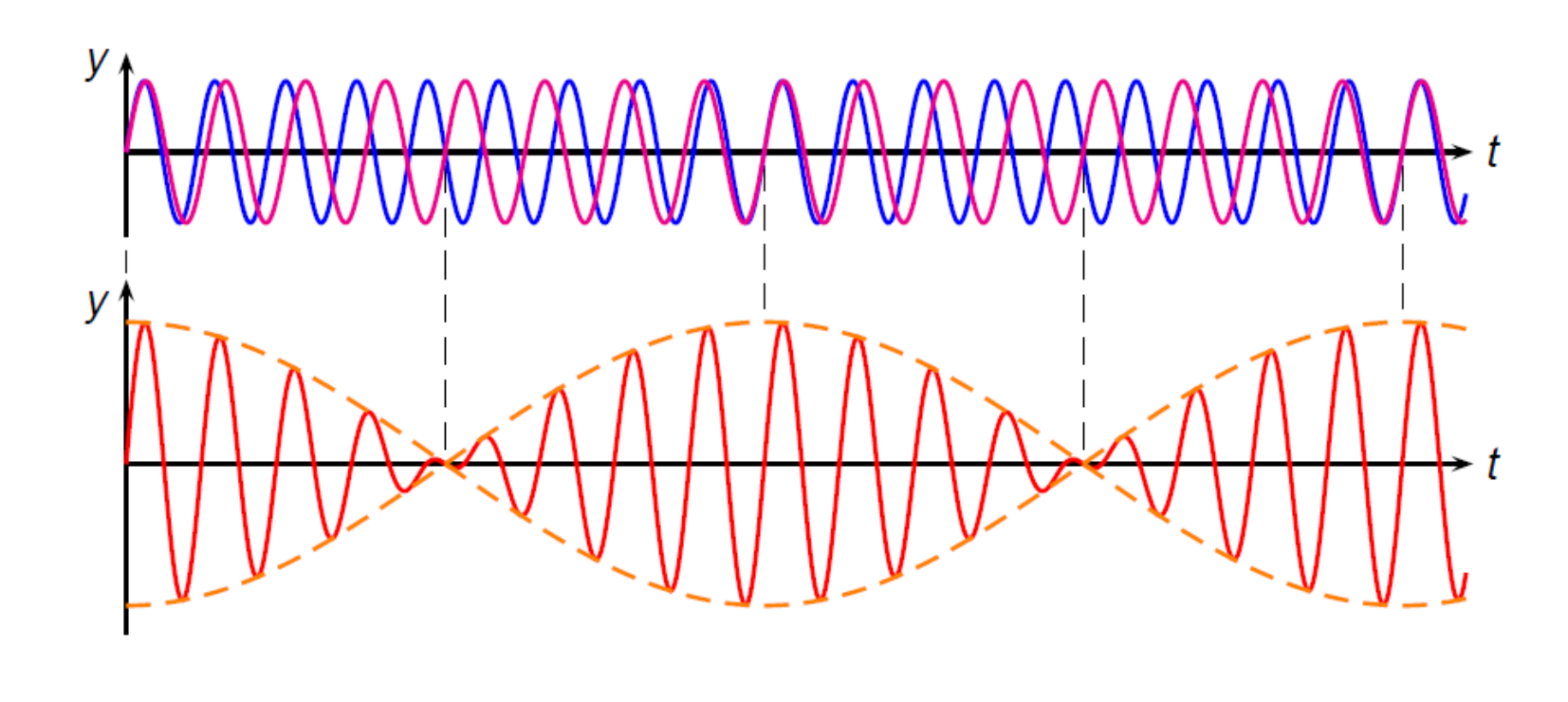
L’onde résultante est alors donnée par :
\[ \boxed{ y_{tot}(t) = y_1(t) + y_2(t) = 2A\cos\left(2\pi \frac{f_1-f_2}{2}t\right)\cdot \sin\left( 2\pi \frac{f_1 + f_2}{2}t \right)} \]
La fréquence de battement est quant à elle donnée par :
\[\boxed{ f_{bat} = \vert f_1 - f_2 \vert} \]
L’intensité d’une onde est égale à l’énergie incidente de l’onde par unité de temps et par unité d’aire \(S\) normale à la direction de propagation.
\[ \boxed{I = {P\over S}} \]
(unité : \(Wm^{-2}\))
Pour une oreille normale, on parle de :
L’intensité variant d’un facteur \(10^{12}\) entre ces valeurs, on introduit une échelle logarithmique :
\[ \boxed{\beta = 10\log{\frac{I}{I_0}}} \]
Où \(I\) est l’intensité mesurée et \(I_0\) une intensité de référence.
En prenant \(I_0 = 10^{-12} Wm^{-2}\), le seuil de sensation douloureuse correspond à
\[ \beta = 10\log(10^{12}) = 120 \space dB \]
L’addition des sources se fait au niveau de l’intensité, par sur les dB.
Deux haut-parleurs produisant chacun un niveau sonore de 80 dB, ne donnerons pas un niveau sonore de 160 dB au total !
On a :
\[ I_{1HP} = 10^8 \cdot 10^{-12} = 10^{-4} Wm ^{-2} \quad\Rightarrow\quad I_{tot} = 2\cdot I_{1HP} = 2\cdot 10^{-4} Wm^{-2} \]
Le niveau sonore perçu par l’auditeur sera donc de :
\[ \beta _{2HP} = 10\log{\frac{2\cdot 10^{-4}}{I_0}} = 83 \space dB \]
Définition
On appelle effet Doppler le phénomène de disparité qui se manifeste entre la fréquence perçue et la fréquence de vibration d’une source lorsqu’il y a un mouvement relatif entre la source et l’observateur.
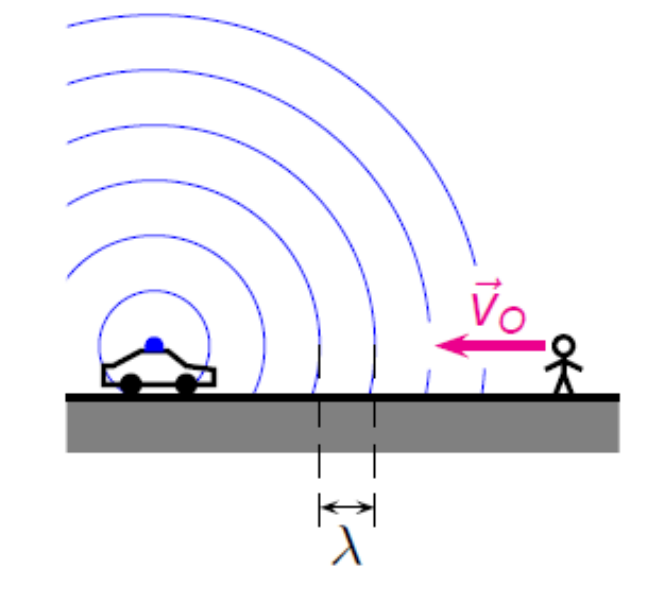
Si la vitesse de l’observateur \(\vec{v}_o\) est dirigée vers la source, la vitesse des ondes sonores semble être de norme \(v'=v + v_o\) , où \(v\) est la vitesse réelle des ondes.
La fréquence perçue \(f'\) semble plus élevée :
\[ f' = {v' \over \lambda} = {v'\over v} f = \frac{v + v_o}{v} f \]
où \(\lambda\) est la longueur d’onde et \(f={v\over \lambda}\)
Si \(\vec{v}_o\) est dirigée à l’opposé de la source, la vitesse des ondes sonores semble être de norme \(v' = v-v_o\) et la fréquence perçue \(f'\) semble plus basse :
\[ f' = {v' \over \lambda} = {v'\over v} f = \frac{v - v_o}{v} f \]
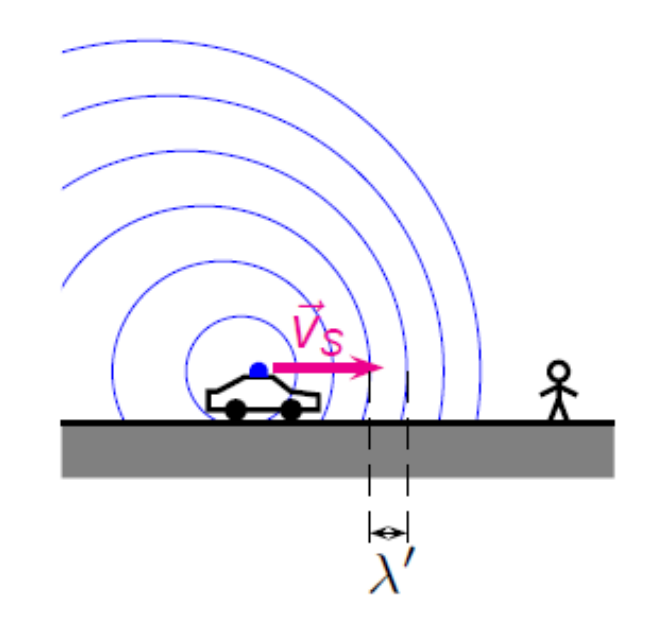
Si la vitesse de la source \(\vec{v}_s\) est dirigée vers l’observateur, la longueur d’onde semble valoir \(\lambda' = {v-v_s\over f}\), où \(v\) est la vitesse de l’onde et \(f\) la fréquence de la source.
La fréquence perçue semble alors plus élevée :
\[ f' = {v\over\lambda'} = {v\over v-v_s} f \]
Si \(\vec{v}_s\) est dirigée à l’opposée de l’observateur, la longueur d’onde semble valoir \(\lambda' = {v+v_s\over f}\).
La fréquence perçue semble alors plus basse :
\[ f' = {v\over \lambda'} = {v\over v+v_s} f \]
Effet Doppler
Soient respectivement \(v_s\) et \(v_o\) les vitesses de la source et de l’observateur par rapport au milieu ambiant. Alors la fréquence perçue \(f'\) par l’observateur est
\[ \boxed {f' = \frac{v\pm v_o}{v\mp v_s} f } \]
Où \(v\) est la vitesse des ondes et \(f\) la fréquence de la source.
L’expression donnant \(f'\) en fonction de \(f\) n’est plus valable si \(v_s>v\) (on aurait sinon une fréquence négative, ce qui n’a pas de sens physique).
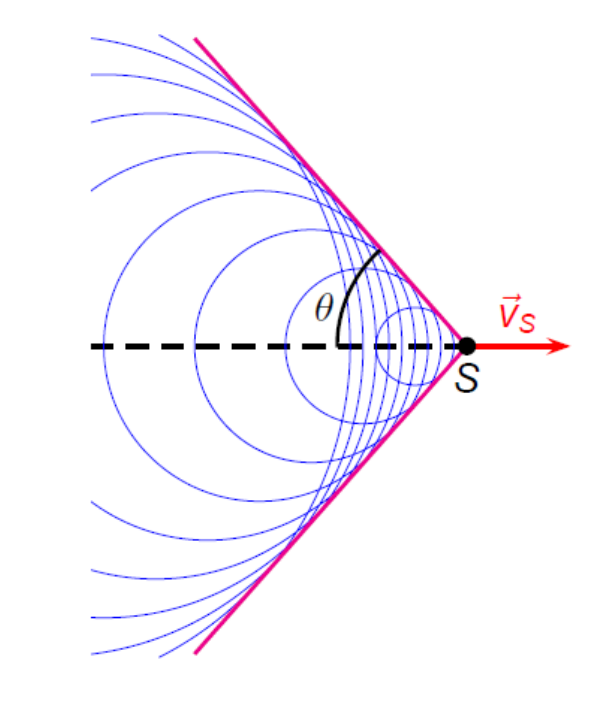
Dans ce cas, la source se trouve à l’extérieur, devant les fronts d’onde émis. On dit qu’elle a passé le mur du son.
Les fronts d’onde ont pour enveloppe la paroi d’une cône.
Sur cette surface conique se concentre l’énergie sonore, il y a formation d’une onde de choc.
L’angle \(\theta\) entre la surface conique et la direction de propagation de la source est donnée par :
\[ \sin\theta = {v_{son}\over v_{source}} \]
Exported with pandoc 2.9.2.1 on Thu Apr 14 2022 at 15:11:21 CEST. @ylked
All informations are given without warranty. All rights reserved ©