Tout objet solide est formé d’un grand nombre d’atome liés entre eux par des forces électriques. La force résultante des forces électriques que subit tout atome dans un objet solide se comporte comme une force de rappel d’un ressort. On peut alors représenter les atomes comme liés entre eux par des ressorts.
Définition
Une onde mécanique est une perturbation d’un milieu, par rapport à un état d’équilibre, se propageant sans transport de matière.
Une perturbation peut être momentanée ou périodique ; Dans le cas d’une perturbation momentanée, on parle d’impulsion.
L’expérience montre que la vitesse de propagation d’une onde dans un milieu matériel : - dépend des propriétés de ce milieu - ne dépend peu ou pas de la source des ondes
La propagation d’une onde est assurée par l’élasticité du milieu. L’étude des forces d’élasticité permet de déterminer la vitesse de propagation.
On considère une impulsion qui se propage à une vitesse \(v\) dans une corde. Soient : - \(F\) la tension dans la corde - \(\mu\) la masse linéique, i.e. la masse par unité de longueur de la corde
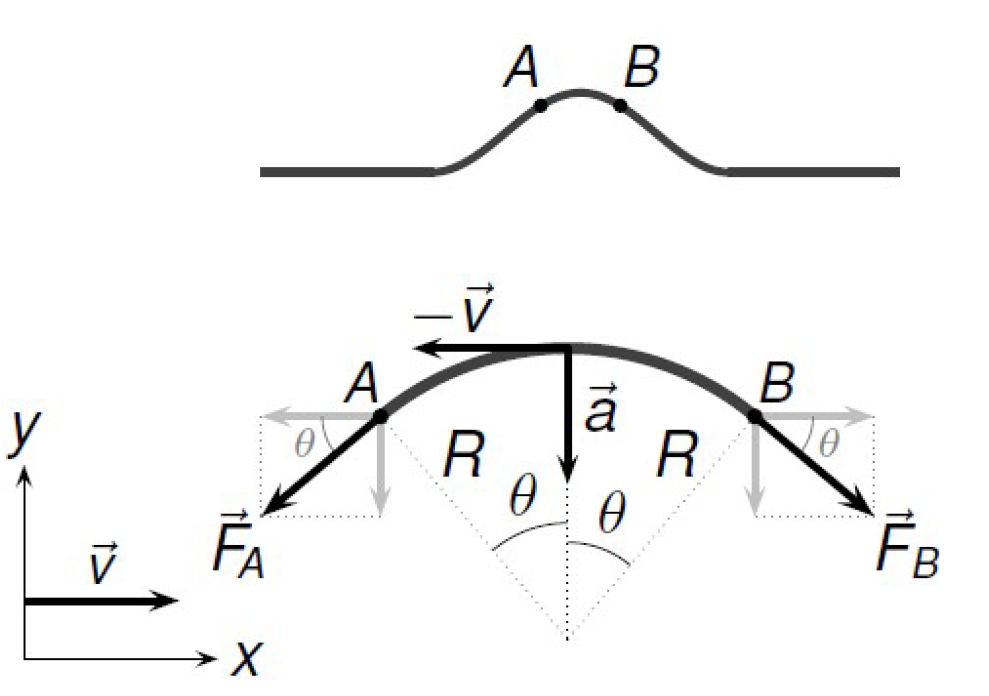
On se place dans un référentiel dans lequel l’impulsion parait immobile. Le référentiel avance donc avec une vitesse \(v\). On prend ensuite un morceau de corde \(AB\) au sommet de l’impulsion, suffisamment petit pour que qu’il puisse être assimilé à un arc de cercle.
On considère la figure suivante : 
En projetant les différents vecteurs sur l’axe \(y\) et en appliquant la deuxième loi de Newton,on a :
\[ F_A \cdot \sin\theta + F_B \cdot \sin\theta = ma \quad \Leftrightarrow \quad 2 F \sin\theta = m \cdot \frac{v^2}{R} \]
où \(R\) est le rayon de l’arc de cercle formé par le morceau de corde \(AB\), \(m\) sa masse et \(a\) son accélération. \(m\) peut d’ailleurs s’écrire comme \(m= \mu \cdot l\). En supposant \(\theta\) petit, \(\sin\theta \cong \theta\). En conséquence :
\[ 2 F \theta = \mu R 2 \theta \frac{v^2}{R} \quad \Leftrightarrow \quad F= \mu \cdot v^2 \]
et donc :
\[ \boxed{ v=\sqrt{\frac{F}{\mu}} } \]
\[ \boxed{ v = \sqrt{E \over \rho} } \]
Où \(E\) est le module d’élasticité de la tige et \(\rho\) sa masse volumique.
\[ \boxed{ v = \sqrt{1\over \kappa \rho} } \]
Où \(\kappa\) est le coefficient de compressibilité du liquide et \(\rho\) sa masse volumique.
Une fonction d’onde \(y(x,t)\) donne l’amplitude de l’onde à la position \(x\) au temps \(t\). Lorsque plusieurs ondes se chevauchent dans une même région, on dit qu’elles sont superposées.
Si l’amplitude est faible, alors la fonction d’onde totale \(y_{tot}\) en tout point est la somme des fonctions d’onde individuelles \(y_i\) :
\[ \boxed{ y_{tot} = \sum_{i=1}^n y_i } \]
On parle d’interférence lorsque plusieurs ondes d’un même type se superposent.
Interférences constructives : Les fonction d’onde sont de même signe ; le déplacement résultant est plus grand que celui de chaque onde. Interférence destructive : Les fonctions d’onde sont de signes opposés ; le déplacement résultant est plus petit que celui de chaque onde.
Quand le milieu dans lequel l’onde se propage change, l’onde est partiellement transmise et partiellement réfléchie.
Il y a alors deux cas de figure possibles :
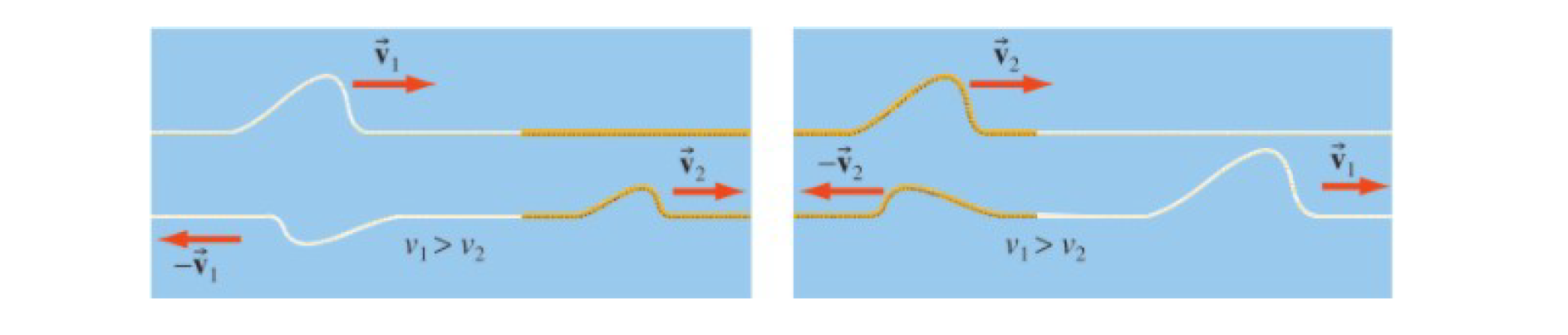
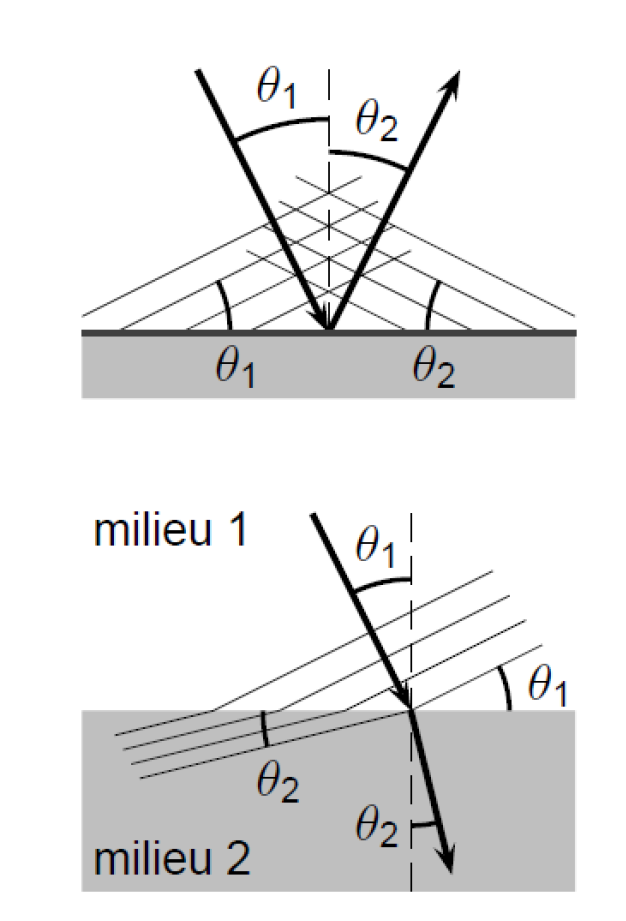
On s’intéresse au changement de direction d’une onde lorsqu’on change son milieu de propagation.
Les fronts d’onde (les lignes reliant les crêtes entre elles) permettent de définir un rayon incident et un rayon réfléchi. On a alors que :
\[ \theta _1= \theta _2 \]
Dans le cas d’ondes sonores, on parle d’écho.
Mathématiquement, une onde progressive peut être décrite par une fonction \(y\) de deux variables : la position \(x\) et le temps \(t\) Dans un référentiel en mouvement avec la perturbation, la perturbation peut être décrite comme une fonction \(g\) de la position : \(y' = g(x')\) Dans un référentiel fixe, la perturbation a la même forme mais elle se déplace à une vitesse de propagation \(v\) ; elle peut s’écrire comme une fonction \(h\) du temps et de la position : \(y = h(x, t)\)
On effectue une transformation entre les deux référentiels :
\[ \left\{ \begin{array}{ll} x' = x - vt \\ y' = y \end{array} \right. \text{ , où } \vec{v} = + v \cdot \vec{u}_x \]
L’onde peut alors s’écrire sous la forme :
\[ y=y'=g(x-vt) \]
En un point donné de la perturbation, \(x-vt=x'\) est constante. La dérivée de cette équation par rapport au temps donne \(\frac{\mathrm{d}x}{\mathrm{d}t} = v\) ce qui montre que la perturbation se propage donc à une vitesse \(v\). Cette vitesse correspond donc à la vitesse de propagation de l’onde.
On appelle fonction d’onde progressive toute fonction \((x,t) \longmapsto g(x \pm vt)\) qui aux deux variables position \(x\) et temps \(t\) fait correspondre l’expression \(g(x \pm vt)\), où \(g\) est une fonction de la variable \(x \pm vt\). On peut alors écrire :
\[ (x,t) \longmapsto x \pm vt \longmapsto g(x \pm vt) \]
Pour un point de coordonnées \(x\) fixe, on a \(y\) en fonction du temps \(t\) :
\[ y(t) = A \sin (\omega t + \varphi_1) \]
avec
Lien entre \(\omega\) et la période \(T\) de l’oscillation :
\[ \omega = \frac{2\pi}{T} = 2\pi \nu \]
où \(\nu = \frac{1}{T}\) est appelée fréquence (Aussi notée \(f\)).
Pour un instant \(t\) fixe, on a en \(y\) en fonction de la position \(x\) :
\[ y(x) = A\sin(kx + \varphi_2) \]
avec
On appelle longueur d’onde \(\lambda\) la distance entre deux crêtes.
Lien avec le nombre d’ondes :
\[ k = \frac{2\pi}{\lambda} \]
Lien entre la longueur d’onde \(\lambda\) et la période \(T\) :
\[ v = \frac{\lambda}{T} = \lambda \nu = \frac{\omega}{k} \]
\[ y(x,t) = A\sin(k(x \pm vt) + \varphi) = A\sin(kx \pm \omega t + \varphi) \]
On appelle onde stationnaire toute onde qui parait immobile.
Les points où la fonction d’onde stationnaire est nulle en tout temps sont appelés les nœuds
Les points où la fonction d’onde est extrémale sont appelés les ventres.
\[ \boxed{ y_{tot}(x,t) = y_1(x,t) + y_2(x,t) = 2A\cos(\omega t + \varphi')\cdot\sin(kx + \varphi) } \]
où \(\varphi=\frac{\varphi_1 + \varphi_2}{2}\) et \(\varphi'=\frac{\varphi_1-\varphi_2}{2}\).
La longueur d’onde et la fréquence des ondes stationnaires dans une core de longueur \(L\), fixée aux extrémités, sont :
\[ \boxed{ \lambda_n ={ 2L\over n} \quad \text{ et } \quad f_n ={ nv \over 2L }\quad n\in \mathbb{N}^* } \]
Où \(v\) est la vitesse de propagation des ondes dans la corde.
Exported with pandoc 2.9.2.1 on Mon Mar 21 2022 at 21:09:32 CET. @ylked
All informations are given without warranty. All rights reserved ©