Chapitre 5 - Oscillations

Oscillation

Définition

Une oscillation est une fluctuation périodique entre deux positions extrêmes autour d’une valeur d’équilibre.

Oscillation harmonique simple

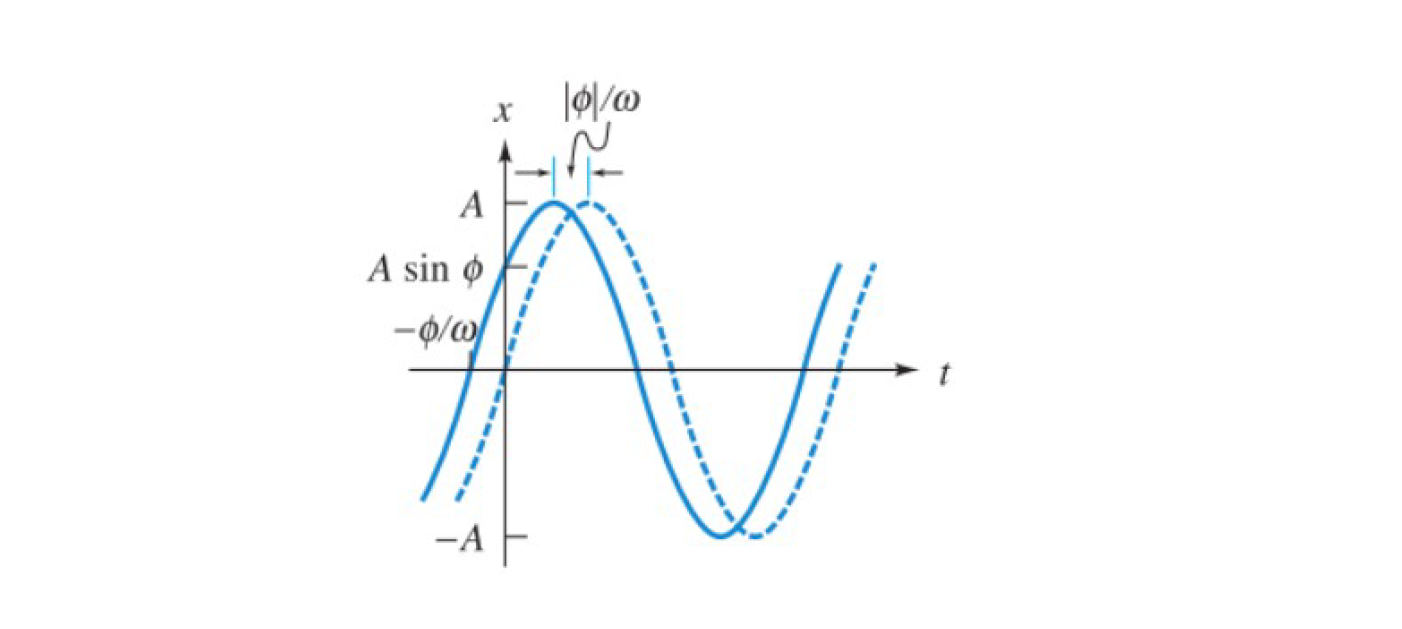
\[ \boxed{ \quad x(t) = A \sin (\omega t + \phi) \quad} \]

où $\phi$ est la phase initiale.

\[ T = \frac{2\pi}{\omega} \quad ,\quad f = \frac{1}{T} \]

Propriétés d’un oscillateur simple

L’amplitude $A$ est constante
La fréquence $f$ et la période $T$ sont indépendantes de l’amplitude
La dépendance temporelle de la grandeur fluctuante peut s’exprimer par une fonction sinusoïdale de fréquence unique.

Unités

L’amplitude $A$ a la même unité que la grandeur oscillante $x(t)$
La fréquence angulaire $\omega$ a comme unité le $rad s^{-1} $
La période $T$ a comme unité la seconde
La fréquence $f$ a comme unité le $Hz$
La constante de phase $\phi$ a comme unité le $rad$.

Vitesse et accélération

\[ \boxed{ \quad v_x(t) = \frac{dx}{dt} = \omega A \cos (\omega t + \phi) \quad} \]

\[ \boxed{ \quad a_x(t) = \frac{dv}{dt} = \frac{d^2 x}{dt ^2} = -\omega ^2 A \sin(\omega t + \phi) \quad} \]

Equation différentielle caractérisant les oscillations harmoniques simples

\[ \boxed{ \quad \frac{d^2x}{dt^2} + \omega ^2 x(t) = 0 \quad} \]

Remarques

L’équation précédente caractérise toutes les oscillations harmoniques simples.

Système bloc-ressort

Soit un système composé composé d’un ressort de constante $k$ et d’un bloc de masse $m$ glissant sans frottement. Le système est disposé tel que montré sur la figure ci-dessous :

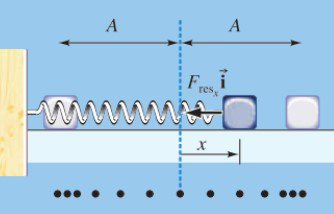
Le système décrit alors un mouvement harmonique simple, dont la pulsation et la période de l’oscillation sont :

\[ \boxed{ \omega = \sqrt{k \over m} } \]

\[ \boxed{ T={2\pi \over \omega} = 2\pi \sqrt{m\over k} } \]