Chapitre 3 - Travail et énergie

Chapitre 3 - Travail et énergieTravailDéfinitionTravail d'une force constante sur un trajet rectiligneDéfinitionForces produisant un travail nulCommentairesTravail totalTroisième loi de NewtonForce de frottementTravail effectué par une force variableTravail du poids sur un déplacement rectiligneTravail effectué par un ressortEffet du travail sur une particuleEnergie cinétique et puissanceEnergie cinétiqueThéorème de l'énergie cinétiquePuissancePuissance en fonction de l'énergieEnergie potentielleConcept d'énergie potentielleForces conservativesPropriétés d'une force conservativeEnergie potentielleDéfinitionFonctions énergie potentielleEnergie (et variation d'énergie) potentielle gravitationnelle à la surface de la terreEnergie (et variation d'énergie) potentielle d'un ressort idéalEnergie potentielle de plusieurs forcesEnergie mécaniqueConservation de l'énergie mécanique - forces conservativesConservation de l'énergie totaleEnergie mécaniqueConservation de l'énergie mécaniqueConservation de l'énergie mécanique - forces non conservativesSystème de particulesCentre de massePosition du centre de masseObjets homogènesObjets symétriques et homogènesObjets plansMouvement du centre de masseVitesse du centre de masseAccélération du centre de massePremière loi de Newton pour un système de particulesEnergie cinétique d'un système de particulesThéorème de l'énergie cinétique pour un système de particulesEnergie mécanique d'un système de particules

Travail

Définition

Le travail d'une force mesure sa contribution à un déplacement.

Travail d'une force constante sur un trajet rectiligne

Définition

$W$ par $\vec{F}$ $\vec{s}$ le long d'un trajet rectiligne est défini par :

W = \vec{F} \cdot \vec{s} = F \cdot s \cdot \cos θ

$\theta$ $\vec{F}$ $\vec{s}$ .

$J = N \cdot m$

Forces produisant un travail nul

Selon la définition, une force non-nulle peut produire un travail nul si :

$\cos\theta=0$ )
$s = 0$ )

Exemple :

Dans le cas d'un mouvement circulaire uniforme, la force centripète n'effectue aucun travail car elle est perpendiculaire au déplacement à chaque instant.

Une force peut donc causer une accélération sans pour autant effectuer un travail.

Commentaires

Travail total

\sum W = \sum {\vec{F}}_{i} \cdot {\vec{s}}_{i}

Troisième loi de Newton

$\vec{F}^{A\rightarrow B} = - \vec{F} ^{B\rightarrow A}$ , et que les points d'applications de chaque force subissent le même déplacement :

W^{A \to B} = - W^{B \to A}

Force de frottement

Comme elle s'oppose au déplacement, son travail est négatif.

W_{f} = f_{c} \cdot s \cdot \cos π = - f_{c} \cdot s

Travail effectué par une force variable

Le travail équivaut à l'aire sous la courbe de la force en fonction du déplacement, ce qui donne la définition suivante :

W = \int_{x_{1}}^{x_{2}} \vec{F} \cdot d \vec{r}

Travail du poids sur un déplacement rectiligne

On a donc

\vec{P} = m \vec{g} = - m g \cdot {\vec{e}}_{y}

et un déplacement quelconque s'exprime sous la forme :

\vec{s} = Δ x \cdot {\vec{e}}_{x} + Δ y \cdot {\vec{e}}_{y} + Δ z \cdot {\vec{e}}_{z}

Ainsi, le travail effectué par la force de gravité est donné par :

W_{g} = m \vec{g} \cdot \vec{s} = - m g \cdot {\vec{e}}_{y} \cdot (Δ x \cdot {\vec{e}}_{x} + Δ y \cdot {\vec{e}}_{y} + Δ z \cdot {\vec{e}}_{z}) = - m g \cdot Δ y

$\Delta y = y_f -y_i$ , on a

W_{g} = - m g \cdot (y_{f} - y_{i})

Le travail du poids dépend donc uniquement des coordonnées verticales initiale et finale et non du trajet suivi.

Travail effectué par un ressort

$\vec{F} _{res}$ exercée par un ressort est donnée par la loi de Hook :

F_{r e s} = - k d

$d$ est l'allongement du ressort par rapport à sa position de repos.

Le travail effectué par un ressort est donc donné par :

W_{r e s} = - \frac{1}{2} k \cdot (x_{f}^{2} - x_{i}^{2})

Le travail effectué par la force de rappel d'un ressort ne dépend donc que des positions initiale et finale.

Effet du travail sur une particule

Si une force effectue un travail non nul sur une particule, on s'attend à ce que la particule accélère.

Mais la vitesse et l'accélération sont des vecteurs alors que le travail est un scalaire. Il faut donc définir une grandeur scalaire qui varie sous l'effet du travail total.

$F$ $x$ . Ainsi

W = F_{x} \cdot Δ x = m \cdot a_{x} \cdot Δ x

$v^2_f = v_i^2 + 2a_x\Delta x$ $a_x\Delta x$ $W$ qui devient alors :

W = \frac{1}{2} m v_{f}^{2} - \frac{1}{2} m v_{i}^{2}

Energie cinétique et puissance

Energie cinétique

Le travail total sur une particule a pour effet de faire varier un scalaire appelé énergie cinétique.

E_{c i n} = \frac{1}{2} m v^{2}

L'énergie cinétique est l'énergie que possède une particule en vertu de sa vitesse.

Théorème de l'énergie cinétique

On peut exprimer le travail total sur une particule par :

\sum W = Δ E_{c i n}

$\sum W$ est le travail total effectué par toutes les forces agissant sur la particule.

Ce théorème est appelé théorème de l'énergie cinétique. Il met en relation l'énergie, une grandeur mesurée en une position, et le travail, mesuré le long d'un déplacement, donc entre deux positions.

Puissance

La puissance mécanique est définie comme une certaine quantité de travail par unité de temps :

P_{m o y} = \frac{Δ W}{Δ t}

$\Delta W$ $\Delta t$ .

watt $W = Js^{-1}$

La puissance d'une force a le même signe que son travail.

$P>0 \Rightarrow$ la force fournit de l'énergie au corps sur lequel elle s'exerce
$P<0 \Rightarrow$ la force retire de l'énergie au corps sur lequel elle s'exerce

$\Delta t \rightarrow 0$ :

P = \frac{d}{d t} W

$\vec{F}$ $d \vec{s}$ $dW = \vec{F} \cdot d \vec{s}$ $\vec{v} = \frac{d}{dt} \vec{s}$ $P=\frac{d}{dt} W = \vec{F} \cdot \frac{d}{dt} \vec{s}$ , on a alors :

P = \vec{F} \cdot \vec{v}

Puissance en fonction de l'énergie

A partir du théorème de l'énergie cinétique, on peut dire que :

\sum P = \frac{d}{d t} E_{c i n}

Donc un corps dont l'énergie cinétique est constante subit une puissance totale nulle.

Plus généralement, la puissance est le taux d'énergie transférée à un autre ou le taux de transformation de l'énergie d'une forme à une autre :

P = \frac{d}{d t} E

C'est la puissance instantanée en fonction de l'énergie.

Energie potentielle

Concept d'énergie potentielle

L'énergie potentielle est l'énergie attribuable aux positions relatives de deux ou de plusieurs particules en interaction.

Forces conservatives

On sait que le travail de la force de gravité ou la force de rappel d'un ressort ne dépend que des positions initiales et finales (et pas du trajet effectué).

On appelle ces forces des forces conservatives.

A l'inverse, le travail de de la force de frottement dépend de la longueur du parcours effectué.

On appelle ce type de forces des forces non conservatives.

Propriétés d'une force conservative

\begin{aligned} W_{C_{1} (A \to B)} = W_{C_{2} (A \to B)} \\ \Rightarrow W_{C (A \to A)} = 0 \end{aligned}

$C_1$ $C_2$ ont deux chemins différents ayants les mêmes points initiaux et finaux.

Il n'y a que peu de forces qui sont conservatives. On peut en dénombrer trois : la force de gravité, la force de rappel d'un ressort et la force électrique.

Energie potentielle

L'énergie potentielle ne peut être définie que pour une force conservative.

$m$ $h$ .

$W = -mg(y_f -y_i) = mgh$

$\Delta \mathcal{E}_{cin}=mgh$ .

$mgh$ .

$\mathcal{E}_{pot,i}-\mathcal{E}_{pot,f}=W_c$ $W_c$ est le travail effectué par la force conservative.

Définition

On définit la variation d'énergie potentielle en fonction du travail effectué par la force conservative correspondante :

Δ E_{p o t} = E_{p o t, f} - E_{p o t, i} = - W_{c}

Fonctions énergie potentielle

$W_g = -mg(y_f-y_i) = -(\mathcal{E}_{pot,f}-\mathcal{E}_{pot,i})$ , on en déduit les formules suivantes.

Energie (et variation d'énergie) potentielle gravitationnelle à la surface de la terre

E_{p o t, g} = m g y

Δ E_{p o t, g} = m g Δ y

$\mathcal{E}_{pot,g} = 0$ $y=0$ , position que l'on peut fixer arbitrairement.

Energie (et variation d'énergie) potentielle d'un ressort idéal

E_{p o t, r e s} = \frac{1}{2} k x^{2}

Δ E_{p o t, r e s} = \frac{1}{2} k (x_{f}^{2} - x_{i}^{2})

Energie potentielle de plusieurs forces

$\Delta\mathcal{E}_{pot}=-W_c$ $W_c$ représente le travail de toutes les forces conservatives.

Par exemple, pour un bloc remontant un plan incliné sous l'effet d'un ressort étiré, il subit alors pendant son trajet, le travail conservatif de la gravité et le travail conservatif du ressort. Le travail conservatif total vaut donc la somme de chaque travail conservatif :

\begin{aligned} W_{C} = W_{g} + W_{r e s} \\ \Rightarrow & E_{p o t} = E_{p o t, g} + E_{p o t, r e s} \\ \Rightarrow & Δ E_{p o t} = Δ E_{p o t, g} + Δ E_{p o t, r e s} \end{aligned}

Energie mécanique

Conservation de l'énergie mécanique - forces conservatives

Lorsque qu'une particule est soumise uniquement à des forces conservatives, on a :

\begin{matrix} \sum W = Δ E_{c i n} \\ Δ E_{p o t} = - W_{C} \\ \sum W = W_{C} \end{matrix}

Conservation de l'énergie totale

\begin{matrix} Δ E_{c i n} + Δ E_{p o t} = 0 \\ \Leftrightarrow \\ E_{c i n, f} + E_{p o t, f} = E_{c i n, i} + E_{p o t, i} \end{matrix}

Energie mécanique

E_{m e c} = E_{c i n} + E_{p o t}

Conservation de l'énergie mécanique

\begin{matrix} Δ E_{m e c} = 0 \\ \Leftrightarrow \\ E_{m e c, f} = E_{m e c, i} \end{matrix}

Conservation de l'énergie mécanique - forces non conservatives

Selon le théorème de l'énergie cinétique, la variation d'énergie cinétique d'une particule dépend de toutes les forces agissant sur la particule, y compris les forces non conservatives.

En séparant ces deux types de forces, le théorème de l'énergie cinétique devient :

\sum W = W_{C} + W_{N C} = Δ E_{c i n}

$\Delta\mathcal{E}_{pot}=-W_C$ , le théorème de l'énergie cinétique peut s'exprimer sous les formes suivantes :

\begin{matrix} Δ E_{c i n} + Δ E_{p o t} = W_{N C} \\ E_{c i n, f} + E_{p o t, f} = E_{c i n, i} + E_{p o t, i} + W_{N C} \\ Δ E_{m e c} = W_{N C} \end{matrix}

Système de particules

Jusqu'à présent, on a modélisé les corps comme étant des particules (des points matériels). Cela fonctionne uniquement pour des mouvements de translation.

Si le mouvement du corps fait intervenir des rotations ou des vibrations, il doit être considéré comme un système de particules.

Centre de masse

Un système est un ensemble bien défini de particules.

Il existe un seul point caractérisant la translation du système de particules dans son ensemble. Il s'appelle le centre de masse (CM).

$\vec{F}$ sur la tige en un point quelconque (a) ou (b), le système subit une rotation. Mais si on l'applique au centre de masse, le seul mouvement observé est une translation. Il se comporte alors comme une particule, comme si toute la masse était concentrée en un point : le centre de masse.

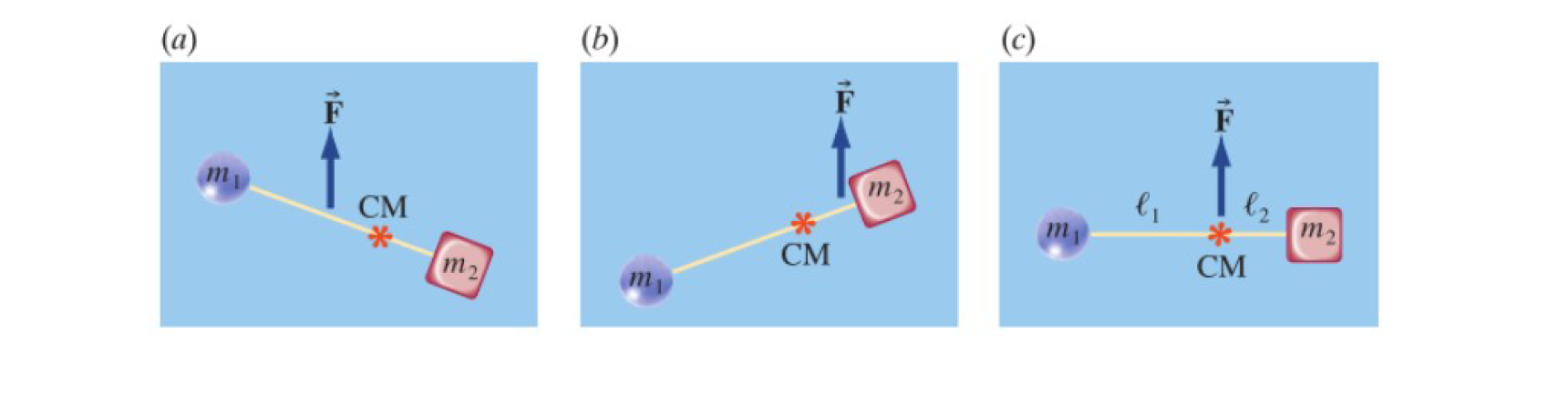
Position du centre de masse

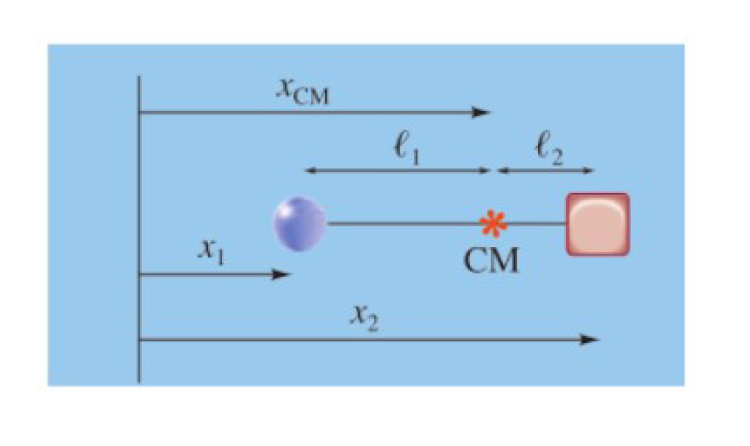
On peut exprimer la position du centre de masse sur la figure ci-dessus, de la manière suivante :

l_{1} = x_{C M} - x_{1} l_{2} = x_{2} - x_{C M}

$m_1 l_1 = m_2 l_2$ , alors :

x_{C M} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}}

$n$ particules en trois dimensions :

\begin{matrix} {\vec{r}}_{C M} = \frac{m_{1} {\vec{r}}_{1} + m_{2} {\vec{r}}_{2} + . . . + m_{n} {\vec{r}}_{n}}{m_{1} + m_{2} + . . . + m_{n}} = \sum_{i = 1}^{n} \frac{m_{i} {\vec{r}}_{i}}{m_{i}} \\ \Rightarrow {\vec{r}}_{C M} = \frac{1}{M_{t o t}} \cdot \sum_{i = 1}^{n} m_{i} {\vec{r}}_{i} \end{matrix}

Objets homogènes

Objets symétriques et homogènes

Le centre de masse se trouve alors au centre de celui-ci ou du moins sur un axe et/ou un plan de symétrie. Il n'y a donc pas besoin de recourir à l'équation pour trouver la position du centre de masse.

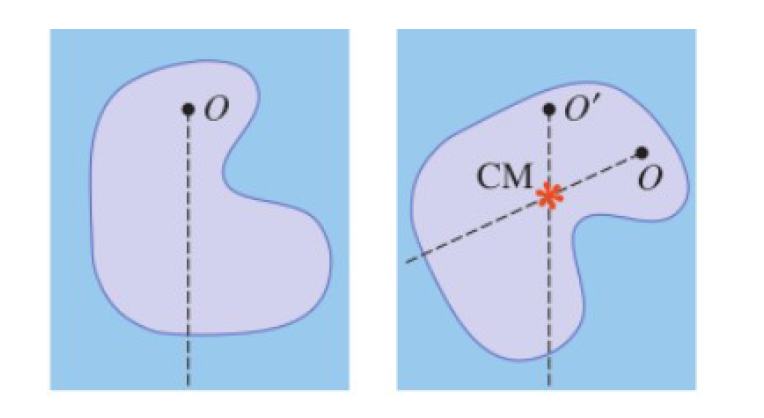
Objets plans

Expérimentalement, il suffit de suspendre l’objet par deux points différents et de tracer à chaque fois la verticale passant par ce point. Le CM se trouve à l’intersection des deux verticales.

Mouvement du centre de masse

Vitesse du centre de masse

{\vec{v}}_{C M} = \frac{1}{M} \cdot \sum_{i = 1}^{n} m_{i} {\vec{v}}_{i}

Accélération du centre de masse

\sum {\vec{F}}_{e x t} = M \cdot {\vec{a}}_{C M}

Première loi de Newton pour un système de particules

\sum {\vec{F}}_{e x t} = 0 \Rightarrow {\vec{a}}_{C M} = {\dot{\vec{v}}}_{C M} = 0

Energie cinétique d'un système de particules

On peut diviser l'énergie d'un système en deux termes : l'énergie du centre de masse et l'énergie par rapport au centre de masse, dite énergie relative.

^e $m_i$ $\vec{r} _i = \vec{r} _{CM} + \vec{r} _i'$ $\vec{r} _{CM}$ $\vec{r} _i'$ est la position de la particule par rapport au CM.

$\vec{v} _i = \vec{v} _{CM} + \vec{v} _i'$

$\mathcal{E}_{cin,i} = \frac{1}{2} m_iv_i^2$ $v_i^2=\vec{v} _i \cdot \vec{v} _i$ , alors :

E_{c i n, i} = \frac{1}{2} m_{i} (v_{C M}^{2} + v_{i}^{' 2} + 2 {\vec{v}}_{C M} \cdot {\vec{v}}_{i}^{'})

$\mathcal{E}_{cin} = \sum_{i=1}^n = \mathcal{E}_{cin,i}$ :

E_{c i n} = \underset{E_{c i n, C M}}{\underset{⏟}{\frac{1}{2} (\sum_{i = 1}^{n} m_{i}) v_{C M}^{2}}} + \underset{E_{c i n, r e l}}{\underset{⏟}{\sum_{i = 1}^{n} \frac{1}{2} m_{i} v_{i}^{' 2}}} + \underset{= 0}{\underset{⏟}{2 {\vec{v}}_{C M} \cdot (\sum_{i = 1}^{n} m_{i} {\vec{v}}_{i}^{'})}}

la dernière partie vaut la vitesse du CM par rapport à lui même, cela vaut donc 0.

L'énergie cinétique d'un système de particules est alors donnée par :

E_{c i n} = E_{c i n, C M} + E_{c i n, r e l}

Théorème de l'énergie cinétique pour un système de particules

$\sum W = \Delta \mathcal{E}_{cin}$ .

$\sum W_i = \Delta \mathcal{E}_{cin,i}$ à chaque particule et additionner toutes les équations obtenues.

\begin{aligned} \sum W = Δ E_{c i n} \\ \Rightarrow & \sum W_{i} = Δ E_{c i n, i} \\ \Rightarrow & \sum W = Δ E_{c i n, C M} + Δ E_{c i n, r e l} \end{aligned}

$\sum W\left( \vec{F}_{int} \right) \neq 0$ .

\Rightarrow \sum W_{i n t} + \sum W_{e x t} = Δ E_{c i n, C M} + Δ E_{c i n, r e l}

La sommes des travaux des forces externes est donc donnée par :

\begin{aligned} \sum W_{e x t} & = Δ E_{c i n, C M} + Δ E_{c i n, r e l} + Δ E_{p o t} \\ = Δ E_{c i n, C M} + Δ E_{i n t} \end{aligned}

Toute force intérieure est conservative (→ énergie potentielle) donc :

\begin{aligned} \sum W_{i n t} = - Δ E_{p o t, i n t} \\ \Rightarrow & E_{i n t} = E_{c i n, r e l} + E_{p o t, i n t} \end{aligned}

$\sum W _{ext} = \Delta\mathcal{E}_{cin,CM} + \Delta\mathcal{E}_{int}$ nous dit qu'un travail extérieur sur un système peut modifier l'énergie cinétique de translation du CM et l'énergie interne du système.

$W_{ext} = 0$ et donc :

Δ E_{c i n, C M} + Δ E_{i n t} = 0

Energie mécanique d'un système de particules

$\mathcal{E}_{mec,tot}$ $n$ particules par :

E_{m e c, t o t} = \sum_{i = 1}^{n} (E_{c i n, i} + E_{p o t, t o t, i})

$\mathcal{E}_{pot,tot,i}$ $i$ .

Lorsque toutes les forces en jeu sont conservatives, le théorème de l'énergie mécanique permet d'écrire

E_{m e c, t o t, B} = E_{m e c, t o t, A} \Leftrightarrow Δ E_{m e c, t o t} = 0

L'énergie mécanique d'un système peut également être subdivisée de la manière suivante :

\begin{aligned} E_{m e c, t o t} & = E_{m e c, C M} + E_{m e c, i n t} \\ = E_{c i n, C M} + E_{p o t, C M} + E_{c i n, r e l} + E_{p o t, i n t} \end{aligned}