Dynamique

De la cinématique à la dynamique

Cinématique $\Rightarrow$$\Rightarrow$ description du mouvement des corps

Dynamique $\Rightarrow$$\Rightarrow$ théorie des causes du mouvement

La théorie newtonienne de la dynamique se résume à trois lois du mouvement, ainsi qu'aux définitions des concepts de force et de masse.

Forces

Concept de force

Définition

On peut définir une force résultante comme toute action qui modifie la vitesse d'une particule. $\Rightarrow$$\Rightarrow$ induit une accélération

Si la résultante est nulle, une force isolée peut être définie comme toute action qui équilibre les autres forces présentes.

Effets de forces

Une force est une interaction entre deux objets. Il est impossible de pousser un objet sans qu'il pousse lui même contre nous.

La force est un concept, il est donc impossible de la voir. On peut toutefois observer et ressentir les effets que nous lui attribuons.

• Une force peut équilibrer d'autre forces ou modifier la vitesse d'une particule.
• Une force provoque presque toujours une déformation. Elle alors être momentanée ou permanente.

Au niveau macroscopique, on distingue deux types de forces :

• les forces de contact (frottements, contraintes)
• les actions à distances (gravité, force électrique, ...)

Quelques forces courantes et mesure

Voici une liste des principales forces macroscopiques que nous rencontrerons dans ce cours :

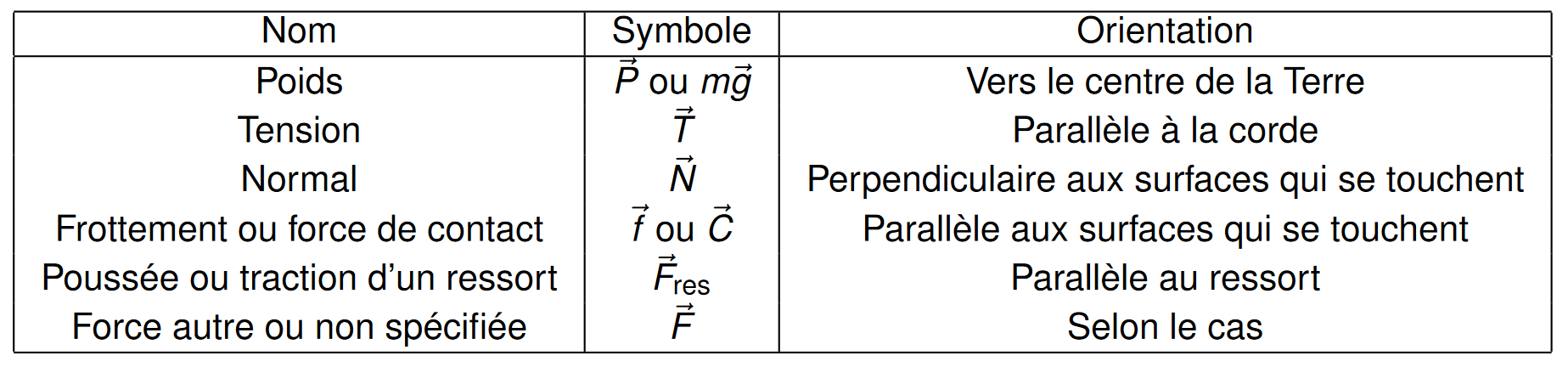
• Le poids est le nom donné à la force gravitationnelle exercée par la Terre sur les objets situés près de sa surface.
• La tension d'une corde est la force de traction exercée par chaque partie de la corde sur les parties voisines et par les extrémités de la corde sur les objets qui y sont attachés.
• La force normale est la force qui empêche deux objets de contact de s'interpénétrer.
• On essaiera de faire la distinction entre le frottement qui est la force qui ralenti deux objets qui glissent l'un contre l'autre ou qui empêche le mouvement d'un objet et la force de contact qui accélère des objets posées sur un camion ou tapis roulant par exemple.
• La force exercée par un ressort vaut $\overrightarrow{F}=-k\cdot \overrightarrow{\mathrm{\Delta }}l$$\vec{F} = -k \cdot \vec{\Delta} l$, où $k$$k$ est la constante de rappel du ressort et $\mathrm{\Delta }l$$\Delta l$ est l'allongement ou la compression du ressort. On voir que la force est opposée à ce dernier (le ressort essaie de retrouver son allongement initial)

Représentation vectorielle d'une force

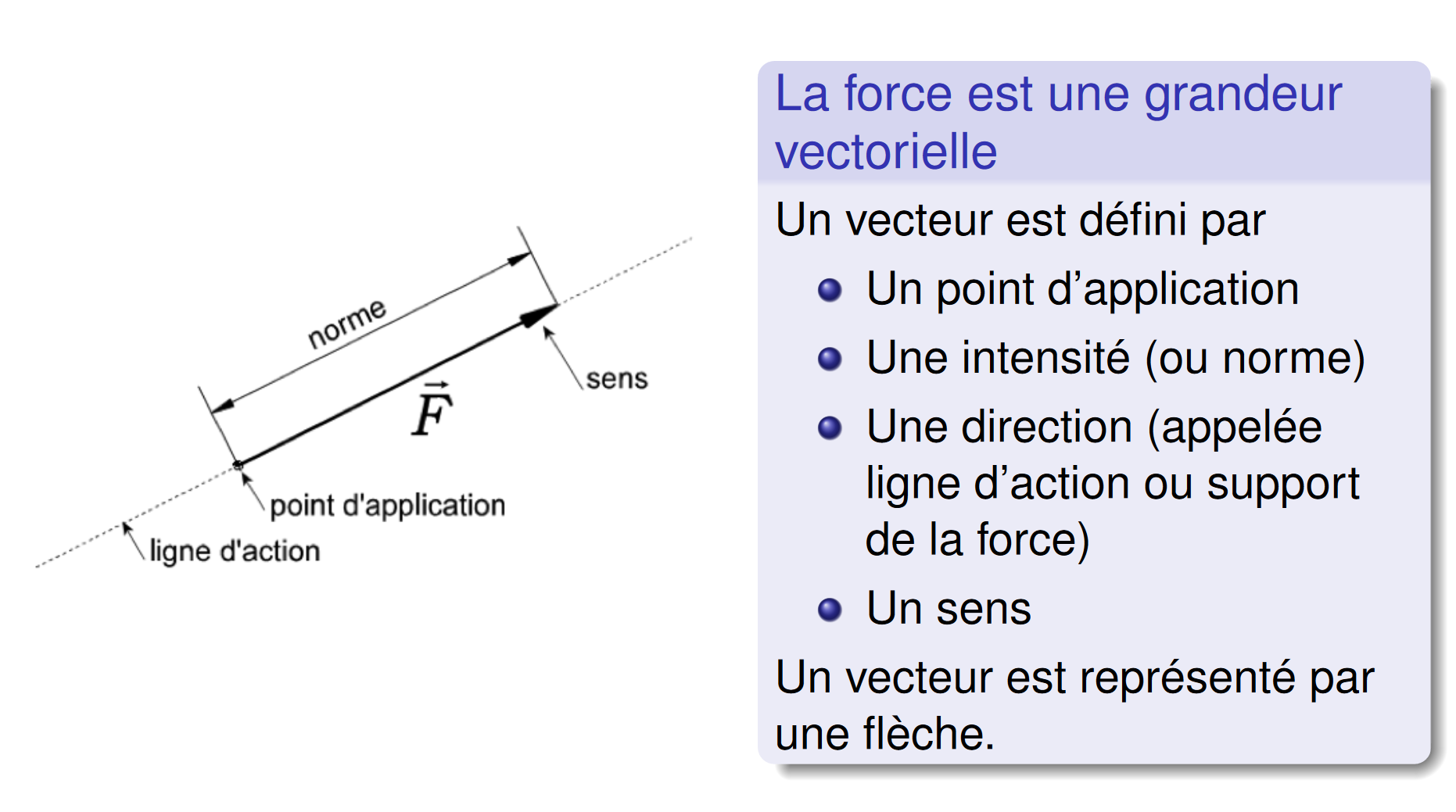
Types de vecteurs

• Vecteur lié (fixe) : vecteur associé à son point d'application
• Vecteur glissant : vecteur dont l'action n'est pas modifiée si on le déplace sur sa ligne d'action. Ce vecteur est lié à une droite (la ligne d'action)
• Vecteur libre : vecteur sans point d'application défini ou avec un point d'application sans importance car ne modifiant en rien l'action de celui-ci.

Les forces sont en général représentées par des vecteurs liés. Dans le cas du solide indéformable en statique, les vecteurs sont des vecteurs glissants.

Implication : une force peut être librement déplacée sur sa ligne d'action.

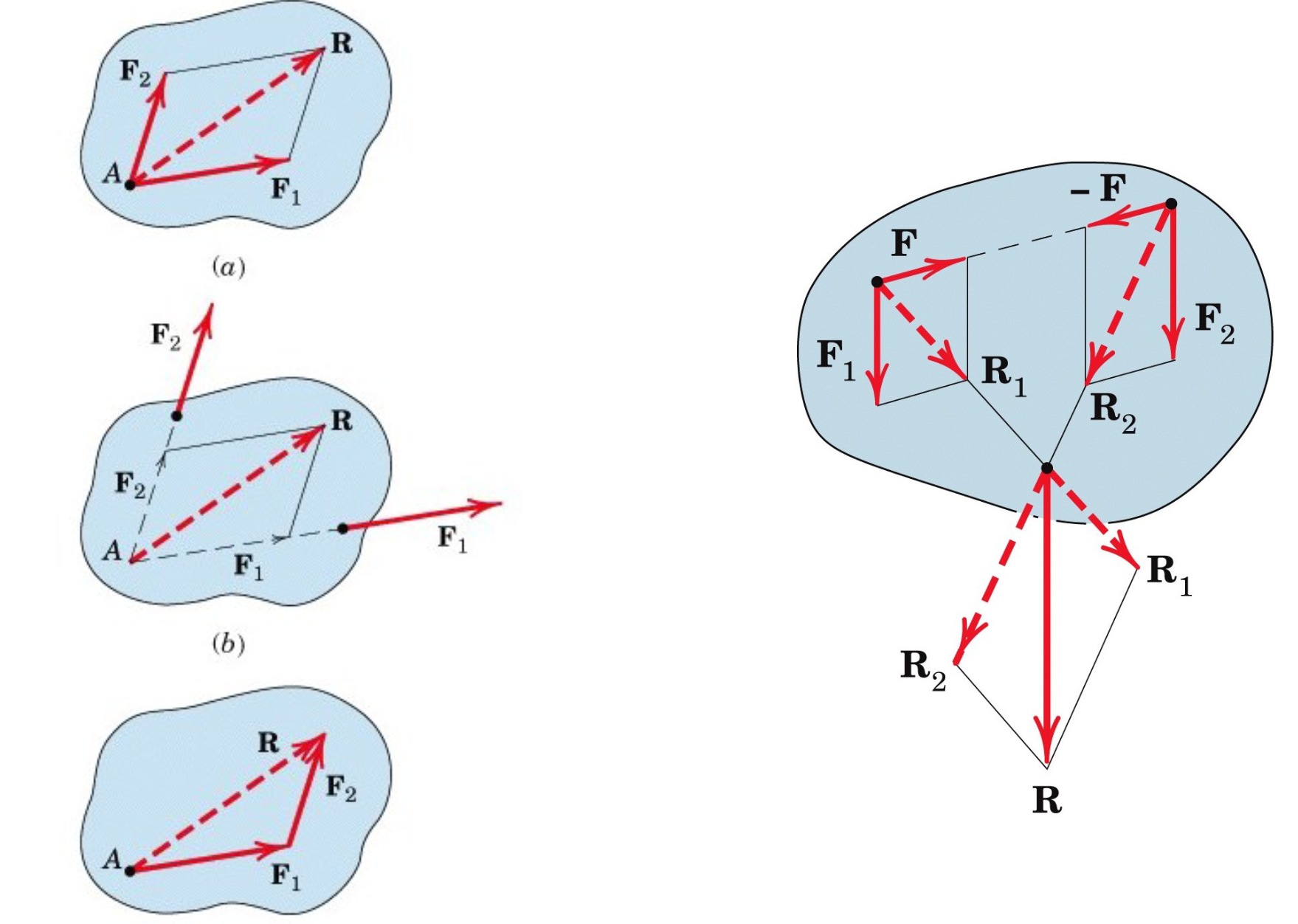
Résultante de deux forces

Masse

Newton a défini la masse comme étant "la quantité de matière" d'un corps. C'est intuitif mais difficile à utiliser.

La deuxième loi de Newton permet de donner une meilleure définition :

Définition

La masse d'un corps est la mesure de son inertie, c'est-à-dire de sa résistance aux variations de vitesse.

2^e loi de Newton

La première loi de Newton indique qu'une force induit un changement de vitesse.

En faisant varier $F$$F$, on remarque que $\parallel \mathrm{\Delta }\overrightarrow{v}\parallel \propto F\cdot \mathrm{\Delta }t$$\|\Delta \vec{v} \| \propto F \cdot \Delta t$

En faisant varier $m$$m$, on trouve que $a\propto \frac{1}{m}$$a \propto \frac{1}{m}$

Ainsi, $a\propto \frac{F}{m}$$a \propto \frac{F}{m}$, donc $f=kma$$f=kma$, où $k$$k$ est une constante de proportionnalité. En unités SI, une force de $1N$$1N$ appliquée sur une masse de $1kg$$1 kg$ provoque une accélération de $1m{s}^{-2}$$1ms^{-2}$, donc $k=1$$k=1$.

Deuxième loi de Newton

La force résultante $\sum \overrightarrow{F}$$\sum{\vec{F} }$ agissant sur une particule de masse $m$$m$ produit une accélération $\overrightarrow{a}=\sum \overrightarrow{F}\cdot m^{-1}$$\vec{a} = \sum{\vec{F} } \cdot m^{-1}$ de même orientation que la force résultante.

Poids

La loi de la gravitation universelle fu énoncée par Newton en 1687 dans le but d'expliquer le mouvement des planètes et la chute des corps à la surface de la Terre.

Loi de la gravitation universelle

Deux objets de masse $m$$m$ et $M$$M$ distants de $r$$r$ exercent chacun l'un sur l'autre une force attractive de module :

Où $G\cong 6.67\cdot {10}^{-11}N\cdot m^2\cdot k{g}^{-2}$$G \cong 6.67 \cdot 10^{-11} N \cdot m^2 \cdot kg^{-2}$

Poids (2)

Le poids d'un objet est donc la force gravitationnelle que le corps céleste le plus proche, habituellement la Terre, exerce sur lui.

La loi de la gravitation appliquée au poids devient donc :

Où $M_T$$M_T$ est la masse de la Terre et $R_T$$R_T$ le rayon de celle-ci.

On écrit généralement cette équation sous la forme vectorielle suivante :

Poids à la surface de la Terre

Où $g=G\cdot M_T\cdot R_T^{-2}\cong 9.81N\cdot k{g}^{-1}$$g=G \cdot M_T \cdot R_T^{-2} \cong 9.81 N \cdot kg^{-1}$

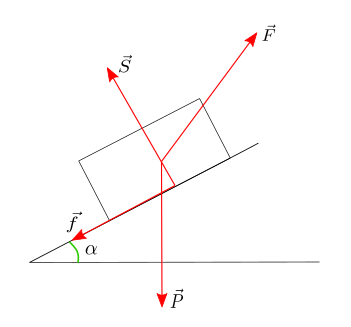
Exemple : plan incliné

3^e loi de Newton

On sait qu'une force est une interaction. Elle est exercée par un corps sur un autre.

Notation : ${\overrightarrow{F}}^{A\to B}$$\vec{F}^{A \rightarrow B}$ est la force exercée par A sur B

Troisième loi de Newton

Les forces que les objets A et B exercent l'un sur l'autre sont de même module et de sens opposés.

A chaque force correspond toujours une force réciproque. Ceci est valable pour toutes les forces, de contact ou à distance, ainsi qu'à chaque instant, que les objets accélèrent ou non.

Les paires de forces action-réaction s'exercent sur des objets différents.

Méthode de résolution

1. Faire un schéma de la situation physique et identifier l'objet auquel on s'intéresse

2. Représenter toutes les forces agissant sur le corps par des objets extérieurs

3. Choisir un système de coordonnées approprié

4. Faire un bilan des forces grâce à la 2^e loi de Newton :

   $$\begin{array}{cc}\sum F_x=m\cdot a_x& \sum F_y=m\cdot a_y\end{array}$$

5. S'il y a plusieurs corps différents, identifier les paires action-réaction et appliquer la 3^e loi de Newton

6. Vérifier la plausibilité des résultats.

Situations d'équilibre

Lorsque la somme des forces s'exerçant sur une particule est nulle, on dit qu'elle est en équilibre de translation.

Si la particule est au repos, elle est en équilibre statique.

Si elle est en mouvement à vitesse constante, elle est en équilibre dynamique.

Dans tous les cas, on a :

Situations hors équilibre

Lorsque la somme des forces agissant sur une particule est non-nulle, les objets accélèrent.

La méthode de résolution est la même mais la résultante des force n'est plus nulle :

Frottements

Considérations générales

Le frottement est une force de contact qui s'oppose au mouvement relatif de deux objet.

En 1508, Léonard de Vinci découvrit que :

• La force de frottement est proportionnelle à la charge
• La force de frottement est indépendante de l'aire de contact.

En 1699, Guillaume Amontons fit les mêmes découvertes, ainsi qu'une troisième :

• La force de frottement est indépendante de la vitesse.

Force de frottement sec

Le frottement sec représente l'action d'une surface rigide sur un solide, action qui s'oppose au mouvement du solide par rapport à la surface.

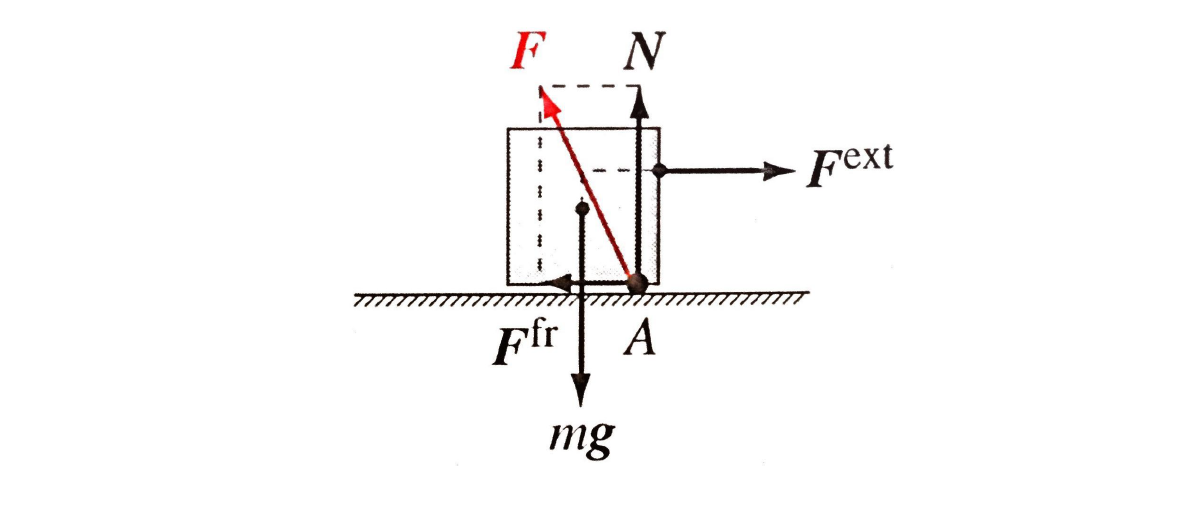
Définition

• La composante de $\overrightarrow{F}$$\vec{F}$ perpendiculaire à la surface de contact est appelée réaction normale $\overrightarrow{N}$$\vec{N}$, c'est une force dirigée vers l'extérieur de la surface.
• La composante de $\overrightarrow{F}$$\vec{F}$ dans le plan tangent au point de contact est appelée force de frottement sec.

Cas statique

Dans un cas statique où le corps est immobile, la force de frottement s'adapte pour annuler l'action des autres forces qui lui sont parallèles.

Vecteur force de frottement en 2D

• Le point d'application se situe quelque part sur la surface de contact
• Sa direction est tangente à la surface au point de contact ${\overrightarrow{F}}^{ext}$$\vec{F}^{ext}$
• son intensité est variable

Intensité

L'intensité de la force de frottement est variable mais a une valeur maximale

Effet de seuil

Lorsque la force de frottement dépasse sa valeur seuil $\parallel {\overrightarrow{F}}_f{\parallel }_{max}=\mu \parallel \overrightarrow{N}\parallel$$\|\vec{F}_f\|_{max}=\mu\|\vec{N}\|$, alors le corps se met en mouvement.

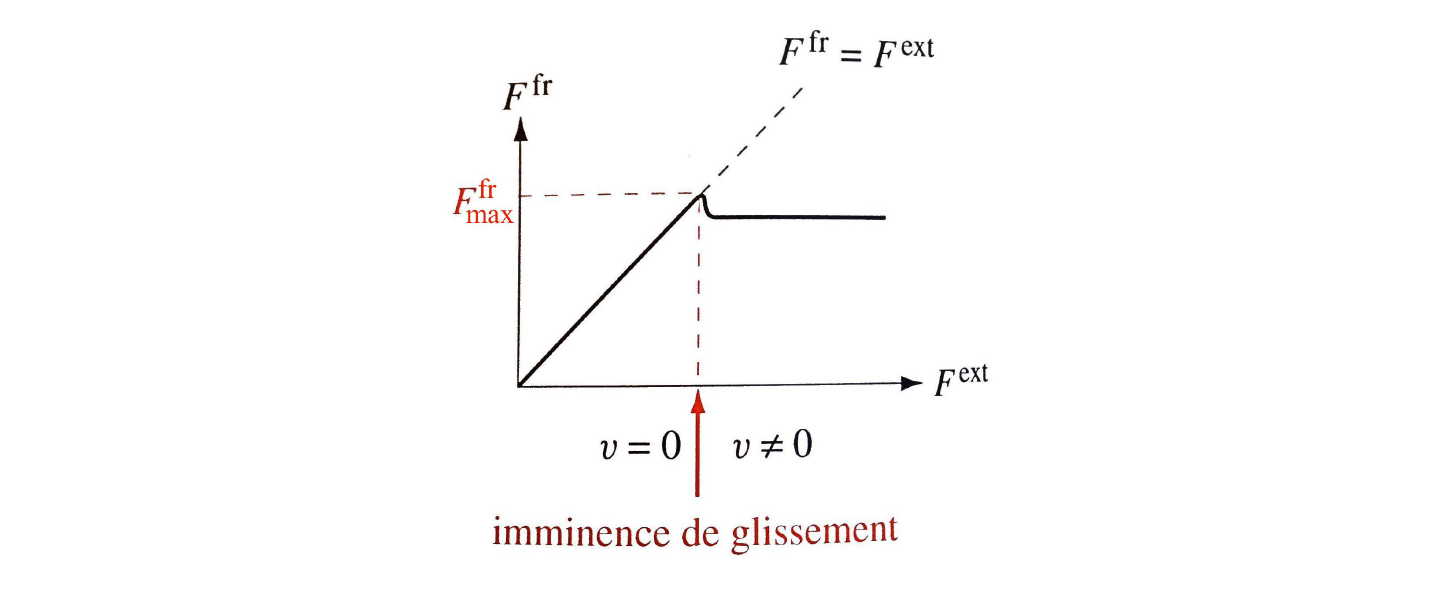
Intensité

L'intensité de la force de frottement sec lorsque l'objet est mobile est alors fixe et vaut :

Où ${\mu }_c$$\mu_c$ est appelé coefficient de frottement cinétique, et ${\mu }_c<{\mu }_s$$\mu_c<\mu_s$.

Cas dynamique

Vecteur force de frottement

Dans les deux cas suivants :

• Cas dynamique ($\Rightarrow \sum \overrightarrow{F}\ne 0\Rightarrow \overrightarrow{a}\ne 0$$\Rightarrow \sum \vec{F} \neq0 \Rightarrow \vec{a} \neq 0$)
• Cas statique où un corps est mobile ($\Rightarrow \sum \overrightarrow{F}=\overrightarrow{0}\Rightarrow \overrightarrow{a}=0$$\Rightarrow\sum \vec{F} =\vec{0} \Rightarrow \vec{a} =0$), mais vitesse du corps non nulle, càd corps qui se déplace à vitesse constante et en ligne droite

La force de frottement sec peut alors s'exprimer entièrement par

Dynamique du mouvement circulaire uniforme

Pour les mouvements rectilignes, le vecteur accélération est parallèle au vecteur vitesse (de même sens ou sens opposé).

Dans un mouvement en deux dimensions, l'accélération peut avoir à la fois une composante tangentielle et une composante normale à la vitesse.

Dans le mouvement circulaire uniforme : l'accélération est purement normale à la vitesse et de module constant.

Accélération centripète

L'accélération centripète est toujours orientée de façon radiale vers le centre du cercle de la trajectoire.

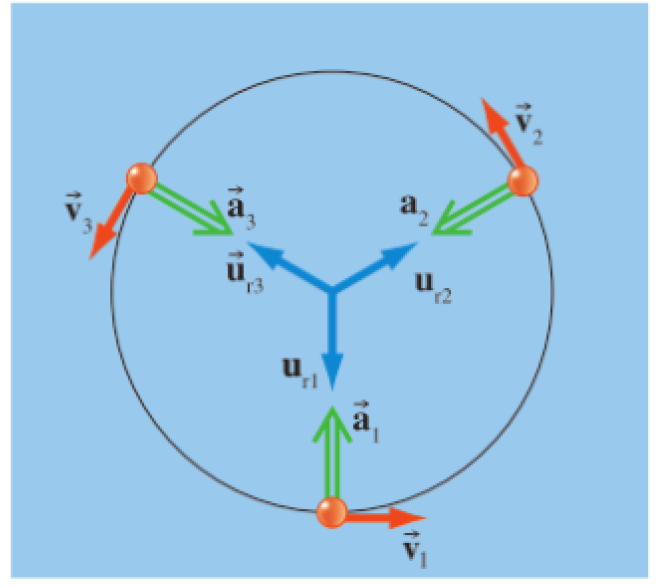
Force centripète

Dynamique du mouvement circulaire non uniforme

Vitesse n'est pas de module constant mais change de direction et de module, l'accélération peut alors être décomposée en une composante tangentielle et une composante centripète (ou normale).

Accélération d'un mouvement circulaire non uniforme

Le premier terme est nommé accélération tangentielle et le deuxième est appelé accélération normale.