Cinématique

Mouvement

La cinématique consiste à décrire la manière dont un objet se déplace dans l'espace et le temps, sans se préoccuper des causes de ce mouvement.

Modélisation

Dans ce chapitre, on va modéliser le mouvement comme s'il était rectiligne → translation

Comme on néglige la rotation, on peut décrire le mouvement de tout objet comme le mouvement d'un seul point.

→ on considère l'objet comme une particule.

Cela ne fonctionne que si la taille, la forme et la structure de l'objet n'importe pas.

Déplacement

Le déplacement est défini comme une différence de deux positions :

Δ \vec{r} = {\vec{r}}_{f} - {\vec{r}}_{i}

$\Delta \vec{r}$ $\vec{r}_i$ $\vec{r}_f$ la position finale.

Si on ne considère qu'une seule dimension, on peut alors écrire :

Δ x = x_{f} - x_{i}

Distance parcourue

La distance parcourue est le trajet réel effectué par l'objet, c'est donc un scalaire positif

exemple

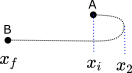
path846

\begin{matrix} Δ x = x_{f} - x_{i} \\ Δ l = | x_{i} - x_{2} | + | x_{2} - x_{f} | \end{matrix}

Vitesse moyenne

$\Delta x$ $\Delta t$ .

On définit alors la vitesse moyenne comme étant :

v_{x_{m o y}} = \frac{Δ x}{Δ t} [m s^{- 1}]

La vitesse scalaire quant à elle est le rapport de la distance parcourue sur le temps :

v_{s c a l_{m o y}} = \frac{Δ l}{Δ t}

Vitesse instantanée

$t$ donné.

Son expression est donnée par :

v_{x} (t) = lim_{Δ t \to 0} \frac{x (t + Δ t) - x (t)}{Δ t} = \frac{d}{d t} x (t) = x^{'} (t)

Accélération moyenne

L'expression de l'accélération moyenne est donnée par :

a_{x_{m o y}} = \frac{Δ v_{x}}{Δ t} [m s^{- 2}]

Accélération instantanée

$t$ donné.

Son expression est donnée par :

a_{x} (t) = lim_{Δ t \to 0} \frac{v_{x} (t + Δ t) - v_{x} (t)}{Δ t} = \frac{d}{d t} v_{x} (t) = v_{x}^{'} (t)

Utilisation des aires

Selon les définitions précédentes, on peut définir la formule suivante :

\begin{matrix} v_{x} = \frac{Δ x}{Δ t} \\ \Rightarrow Δ x = v_{x} \cdot Δ t = \int_{t_{1}}^{t_{2}} v_{x} d t \end{matrix}

Cela implique que l'aire sous le graphe de la vitesse nous donne la différence de position (mais pas la position elle-même!)

De la même manière on a pour l'accélération :

\begin{matrix} a_{x} = \frac{Δ v_{x}}{Δ t} \\ \Rightarrow Δ v_{x} = a_{x} \cdot Δ t = \int_{t_{1}}^{t_{2}} a_{x} d t \end{matrix}

L'aire sous le graphe de l'accélération nous donne bien la différence de vitesse.

Règle de Merton

On considère :

\begin{matrix} t_{i} = 0 s, t_{f} = t \\ a_{x} = a_{x_{m o y}} \end{matrix}

On pose alors :

équation de la vitesse

v_{x} (t) = a_{x} \cdot t + v_{x_{0}}

équation de la position

x (t) = \frac{1}{2} a_{x} \cdot t^{2} + v_{x_{0}} \cdot t + x_{0}

Position dans l'espace

$x$ trois scalaire $(x,y,z)$ que l'on regroupe en un vecteur position qui relie l'origine du système de coordonnées à la position de la particule.

Position

\begin{matrix} \vec{r} = (\begin{matrix} x \\ y \\ z \end{matrix}) = x \cdot {\vec{e}}_{x} + y \cdot {\vec{e}}_{y} + z \cdot {\vec{e}}_{z} \end{matrix}

Déplacement

Δ \vec{r} = \vec{r_{2}} - \vec{r_{1}} = Δ x \cdot {\vec{e}}_{x} + Δ y \cdot {\vec{e}}_{y} + Δ z \cdot {\vec{e}}_{z}

Trajectoire

$\vec{r_i}$ dans l'espace

Vitesse dans l'espace

Vitesse moyenne

{\vec{v}}_{m o y} = \frac{Δ \vec{r}}{Δ t} = \frac{Δ x}{Δ t} \cdot {\vec{e}}_{x} + \frac{Δ y}{Δ t} \cdot {\vec{e}}_{y} + \frac{Δ z}{Δ t} \cdot {\vec{e}}_{z}

Vitesse instantanée

\vec{v} = \frac{d}{d t} \vec{r} = x^{'} \cdot {\vec{e}}_{x} + y^{'} \cdot {\vec{e}}_{y} + z^{'} \cdot {\vec{e}}_{z}

Accélération dans l'espace

Accélération moyenne

{\vec{a}}_{m o y} = \frac{Δ \vec{v}}{Δ t} = \frac{Δ v_{x}}{Δ t} \cdot {\vec{e}}_{x} + \frac{Δ v_{y}}{Δ t} \cdot {\vec{e}}_{y} + \frac{Δ v_{z}}{Δ t} \cdot {\vec{e}}_{z}

Accélération instantanée

\vec{a} = \frac{d}{d t} \vec{v} = v_{x}^{'} \cdot {\vec{e}}_{x} + v_{y}^{'} \cdot {\vec{e}}_{y} + v_{z}^{'} \cdot {\vec{e}}_{z}

$\vec{v}$ et/ou sa norme.

Equation de la cinématique à accélération constante

Equation de la vitesse

\vec{v} = {\vec{v}}_{0} + \vec{a} \cdot t

Equation de la position

\vec{r} = {\vec{r}}_{0} + {\vec{v}}_{0} \cdot t + \frac{1}{2} \vec{a} \cdot t^{2}

Mouvement circulaire uniforme

Dans un MCU, la norme de la vitesse est constant.

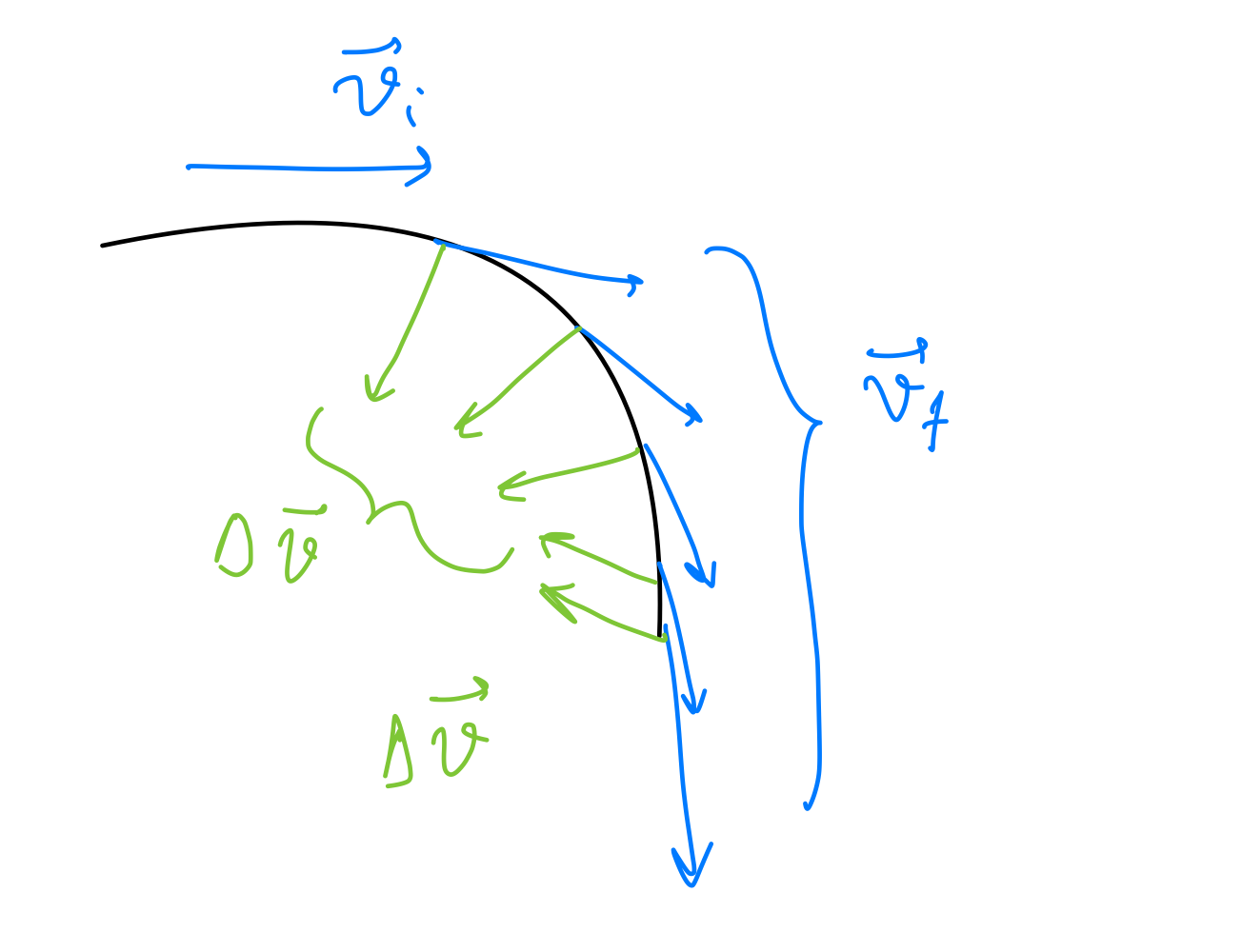
20211021_123148240_iOS

Δ \vec{v} = \vec{v_{f}} - \vec{v_{i}}

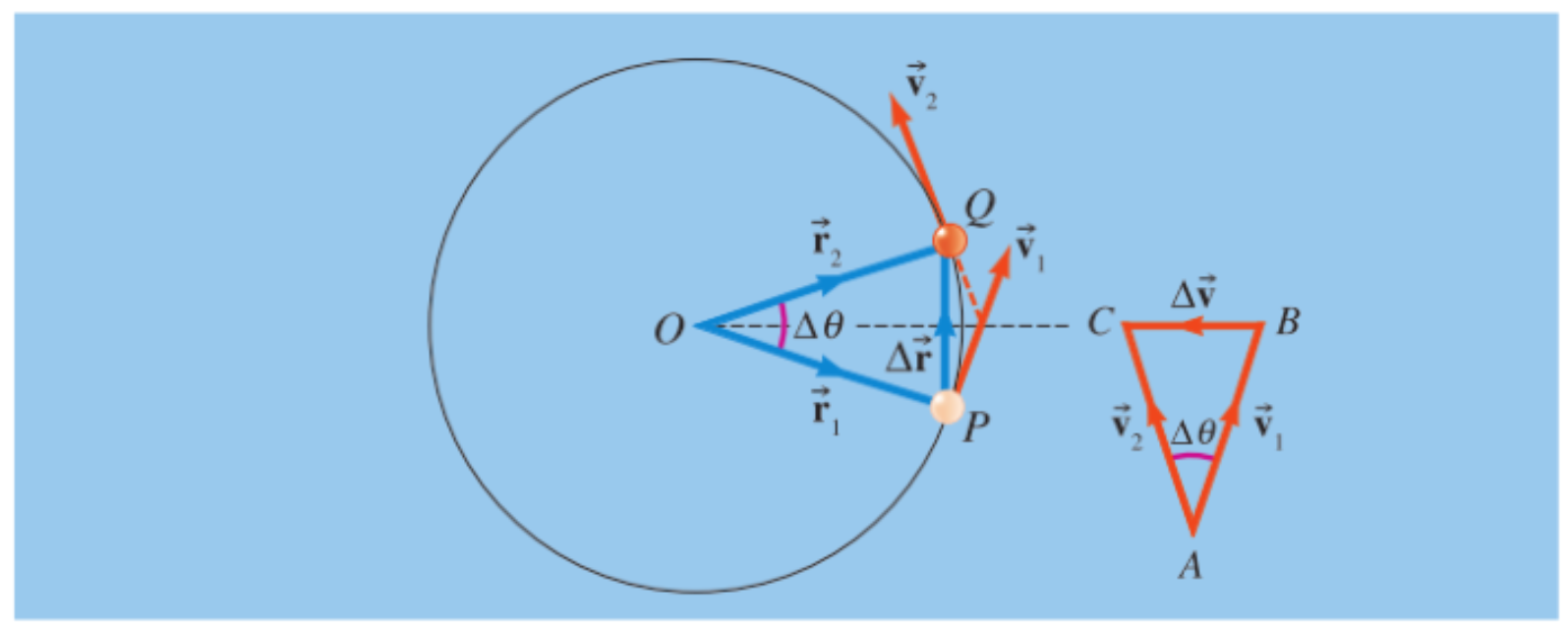
2021-10-21 14_13_32-1-Cinématique.pdf - Firefox Developer Edition

$\vec{a}$ d'orientation $\vec{v}$

$\Delta \vec{v}$ $\vec{a} = \frac{\Delta \vec{v} }{\Delta t}$ également.

l'accélération dirigée vers le centre du cercle est appelée l'accélération centripète.

C'est une accélération instantanée.

$R$ $\vec{v}$ $v = \norm{\space \vec{v}\space }$ est constant, décrit un mouvement circulaire uniforme.

$\vec{v}$ $\vec{r}$ . Grâce au théorème de Thalès, on peut alors écrire :

\begin{aligned} \frac{‖ Δ \vec{r} ‖}{R} = \frac{‖ Δ \vec{v} ‖}{v} \\ \Rightarrow & ‖ Δ \vec{v} ‖ = \frac{v}{R} \cdot ‖ Δ \vec{r} ‖ \end{aligned}

$\Delta t$ $\Delta \theta$ des vecteurs position et vitesse le sera aussi.

$\Delta \vec{r}$ $\norm{\Delta \vec{r}\space }= v \cdot \Delta t$

Accélération centripète

‖ {\vec{a}}_{r} ‖ = \frac{‖ Δ \vec{v} ‖}{Δ t} = \frac{v^{2}}{R}

Accélération centripète vectorielle

{\vec{a}}_{r} = \frac{- v^{2}}{R} \cdot {\vec{u}}_{r}

Période

période $T$ est le temps nécessaire à la particule pour effectuer une révolution (tour complet)

$\Delta \vec{r} = 2 \pi R$ $\Delta t = \frac{\Delta r}{v}$

On en déduit que la période vaut :

T = \frac{2 π R}{v}

$v = \frac{2\pi R}{T}$ . Ainsi :

a_{r} = \frac{4 π^{2} R}{T^{2}}

Mouvement circulaire non-uniforme

Comme on l'a vu plus tôt, une accélération, en plus de pouvoir être une variation de direction de la vitesse, elle peut aussi être une variation de sa norme.

Cette variation de la norme de la vitesse est appelée accélération tangentielle.

Sur un trajectoire généralisée, la vitesse peut tant varier en module qu'en orientation. C'est ce qu'on appelle le mouvement circulaire non-uniforme.

Repère n-t

$\vec{e_n}$ $\vec{e_t}$ est tangentiel à celle-ci.

$\vec{e_n}$ $\vec{e} _t$ $\vec{v}$ .

Vitesse et accélération dans le repère n-t

Vitesse

Dans le repère n-t, la vitesse s'exprime par :

\begin{aligned} \vec{v} (t) = v (t) \cdot {\vec{e}}_{t} + 0 \cdot {\vec{e}}_{n} \end{aligned}

$v(t) = \abs{\space \vec{v} (t)}$

Accélération

Dans le repère n-t, l'accélération s'exprime par :

\begin{aligned} \vec{a} (t) & = a_{t} (t) \cdot {\vec{e}}_{t} + a_{n} (t) \cdot {\vec{e}}_{n} \\ = \frac{d}{d t} v (t) \cdot {\vec{e}}_{t} + \frac{v^{2} (t)}{R (t)} \cdot {\vec{e}}_{n} \end{aligned}

$v(t) = \norm{\space \vec{v} (t)}$