Une matrice est un tableau de nombres :
\[ A=\begin{pmatrix} A_{11} & A_{12} & ... & A_{1n}\\A_{21} & A_{22} & ... & A_{2n}\\...&...&A_{ij}&...\\A_{m1}&A_{m2}&...&A_{mn}\end{pmatrix} \]
Par convention, on désigne un élément particulier d’une matrice en indiquant d’abord le numéro de sa ligne puis de sa colonne.
Ainsi, \(A_{ij}\) Désigne l’élément à la \(i\)e ligne et la \(j\)e colonne de la matrice \(A\).
On parle d’une matrice d’ordre \(m\times n\) quand la matrice possède \(i\) lignes et \(j\) colonnes
Ce sont des matrices d’ordre \(n\times n\), dites d’ordre \(n\)
Matrice d’ordre \(n\) telle que :
\[ I=\begin{pmatrix}1&0&...&0\\0&1&...&0\\...&...&...&...\\0&0&...&1\end{pmatrix} \]
On écrit aussi :
\[ (I)_{ij} = \delta_{ij} \quad \text{ avec } \quad \left\{ \begin{array}{l} 0 \text{ si } i\neq j\\1 \text{ si } i = j \end{array} \right. \]
Une matrice carrée est dite symétrique si :
\[ A_{ij} = A_{ji} \quad , \space \forall ij \]
Une matrice carrée est dite antisymétrique si :
\[ A_{ij} = -A_{ji} \quad , \space \forall ij \]
\[ A=B \quad \Leftrightarrow \quad A_{ij}=B_{ij} \quad , \space \forall ij \]
Soient \(A\) et \(B\) deux matrices d’ordre \(m\times n\). L’addition de \(A\) et \(B\), notée \(A+B\), donne une nouvelle matrice \(C\) d’ordre \(m\times n\) définie par
\[ \boxed{\quad C=A+B \quad \text{ t.q. } \quad C_{ij} = (A+B)_{ij} = A_{ij} + B_{ij} \quad} \]
Soient \(A,B,C\) trois matrices d’ordre \(m\times n\).
\[ \boxed{ (A+B) + C = A+ (B+C) } \]
\[ \boxed{ A+B = B+A } \]
\[ \boxed{ 0_{m\times n} = \begin{pmatrix}0&0&...&0\\0&0&...&0\\...&...&0&...\\0&0&...&0\end{pmatrix} } \]
\[ \boxed{ A + (-A) = 0_{m\times n} } \]
Soit \(A\) une matrice d’ordre \(m\times n\), la multiplication de \(A\) par le scalaire \(\lambda\) donne une nouvelle matrice \(C\) d’ordre \(m\times n\) définie par
\[ \boxed{ C=\lambda \cdot A \quad \text{ t.q. }\quad C_{ij} = (\lambda \cdot A)_{ij} = \lambda \cdot A_{ij} } \]
Soient \(A\) et \(B\) deux matrices d’ordre \(m\times n\) et soient \(\lambda,\mu\in\mathbb{R}\) deux scalaires.
\[ \boxed{ \lambda \cdot (\mu\cdot A) = (\lambda \cdot \mu) \cdot A } \]
\[ \boxed{ \begin{align*} &\lambda \cdot (A + B) = \lambda A + \lambda B \\ &(\lambda + \mu) \cdot A = \lambda A + \mu A \end{align*} } \]
Soient deux matrices A et B, telles que \(A\) est d’ordre \(m\times n\) et \(B\) est d’ordre \(n\times p\), le produit de \(A\) par \(B\) donne alors une nouvelle matrice \(C\) d’ordre \(m\times p\) définie par :
\[ \boxed{ C=A\cdot B \quad \text{ t.q. }\quad C_{ij} = (A\cdot B)_{ij} = \sum_{k=1}^n A_{ik} \cdot B_{kj} } \]
\[ \boxed{ (A\cdot B) \cdot C = A\cdot (B\cdot C) } \]
\[ \boxed{ A \cdot (B+C) = A\cdot B + A\cdot C } \]
\[ \boxed{ A\cdot I = I\cdot A = A } \]
avec \(I\) t.q. \(I_{ij}=\delta_{ij}\).
Attention : Le produit matriciel n’est pas commutatif. Ainsi ;
\[ \boxed{ A\cdot B \neq B\cdot A } \]
Toutefois, pour une matrice \(A\) donnée, il est possible de trouver une matrice \(B\) telle que \(AB=BA\). On dit alors que les matrices commutent.
Soit une matrice \(A\) d’ordre \(n\times m\). La transposée de \(A\), notée \(A^t\), est une matrice d’ordre \(m\times n\) définie par :
\[ \boxed{ (A^t)_{ij} = A_{ji} } \]
\[ \boxed{ \begin{align*} &(\lambda A)^t = \lambda A^t \\\\ & (A+B)^t = A^t + B^t \end{align*} } \]
\[ \boxed{ {(A^t)}^t = A } \]
\[ \boxed{ (A\cdot B)^t = B^t \cdot A^t } \]
Soit \(\mathbb{R}^m = \mathbb{R} \times \mathbb{R} \times ...\times \mathbb{R}\) l’ensemble des m-tuples de \(\mathbb{R}\)
Soit aussi \(\left\{ \vec{v}_1 , \vec{v}_2, ..., \vec{v}_n \right\}\) une famille de \(n\) vecteurs de \(\mathbb{R}^m\)
On dira alors que \(\vec{v}_i \in \mathbb{R} ^m \quad , \space \forall i\)
On appelle combinaison linéaire des vecteurs \(\vec{v}_i\) l’expression
\[ \boxed{\quad\sum_{i=1}^{n} \lambda_i \vec{v}_i = \lambda _1 \vec{v}_1 + \lambda _2 \vec{v}_2 + ... + \lambda _n \vec{v}_n\quad } \]
avec \(\lambda _i \in \mathbb{R}\)
De plus, la famille \(\left\{ \vec{v}_1 , \vec{v}_2, ..., \vec{v}_n \right\}\) est dite linéairement indépendante si et seulement si
\[ \boxed{\quad\sum_{i=1}^n \lambda_i \vec{v}_i = 0 \quad \Rightarrow \quad \lambda_i = 0 \quad , \space \forall i\quad} \]
Dans \(\mathbb{R}^m\), il y a au maximum \(m\) vecteurs indépendants. Cela signifie que tous les vecteurs de \(\mathbb{R}^m\) peuvent s’écrire comme une combinaison linéaire d’une famille de \(m\) vecteurs indépendants. Ceci amène à la définition suivante :
Toute famille de vecteurs indépendants de \(\mathbb{R}^m\) constitue une base de \(\mathbb{R}_m\)
Soit \(\mathcal{B} = \left\{ \vec{v}_1 , \vec{v}_2, ..., \vec{v}_n \right\}\) une base de \(\mathbb{R}^m\), alors par la définition même d’une base, tout vecteur \(\vec{w} \in \mathbb{R}^m\) pourra s’écrire comme une combinaison linéaire des vecteurs de \(\mathcal{B}\) :
\[ \vec{w} = \sum_{i=1}^n \lambda_i \vec{v}_i \]
On dira alors que les \(\lambda_i\) sont les composantes de \(\vec{w}\) dans la base \(\mathcal{B}\), et on utilisera la notation matricielle suivante :
\[ \vec{w} = \begin{pmatrix} \lambda _1\\\lambda_2\\\vdots \\\lambda_n\end{pmatrix}_{\mathcal{B}} \]
De plus, la décomposition de \(\vec{w}\) sur la base \(\mathcal{B}\) est unique
Autrement dit, Si \(\vec{w} = \sum_{i=1}^n \lambda_i\vec{v}_i\) et \(\vec{w} = \sum_{i=1}^n \mu_i\vec{v}_i\), alors \(\lambda_i = \mu_i \quad , \space \forall i\)
Démonstration
Supposons que, dans la base $ = $\(\left\{ \vec{v}_1 , \vec{v}_2, ..., \vec{v}_n \right\}\), nous ayons
\[ \vec{w} = \sum_{i=1} ^n \lambda_i\vec{v}_i \quad \text{ mais aussi } \quad \vec{w} = \sum_{i=1} ^n \mu_i\vec{v}_i \]
Alors,
\[ \begin{align*} & \sum_{i=1}^n \lambda_i \vec{v}_i = \sum_{i=1}^n \mu_i \vec{v}_i \\\\ \Leftrightarrow \quad& \sum_{i=1}^n \lambda_i\vec{v}_i - \sum_{i=1}^n \mu\vec{v}_i = 0\\\\ \Leftrightarrow \quad & \sum_{i=1}^n\lambda\vec{v}_i - \mu_i\vec{v}_i = \sum_{i=1}^n (\lambda_i - \mu_i) \cdot \vec{v}_i = 0 \\\\ \Leftrightarrow \quad &\boxed{\lambda_i = \mu_i} \quad \Box \end{align*} \]
Une application linéaire de \(\mathbb{R}^n \rightarrow \mathbb{R}^m\) est une opération qui transforme un vecteur à \(n\) composantes en un autre vecteur à \(m\) composantes et qui respecte la propriété suivante :
\[ \boxed{f(\lambda \vec{x}_1 + \vec{x}_2) = \lambda \cdot f(\vec{x}_1) + f (\vec{x}_2) \quad , \space \forall \vec{x}_1,\vec{x_2} \in \mathbb{R}^n} \]
Soit \(f\) une application linéaire telle que :
\[ \begin{align*} f :\space \mathbb{R}^n &\longmapsto \mathbb{R}^m\\ \vec{x} &\longmapsto \vec{y} = f(\vec{x}) \end{align*} \]
Soient aussi \(\mathcal{B}_n\) une base de \(\mathbb{R}^n\) et \(\mathcal{B}_m\) une base de \(\mathbb{R}^m\).
On note alors
\[ X = \begin{pmatrix}x_1\\\vdots \\x_n\end{pmatrix} _{\mathcal{B}_n} \quad \text{les composantes de } \vec{x} \text{ dans la base } \mathcal{B}_n \]
\[ Y = \begin{pmatrix}y_1\\\vdots \\y_m\end{pmatrix} _{\mathcal{B}_m} \quad \text{les composantes de } \vec{y} \text{ dans la base } \mathcal{B}_m \]
Puisque \(f\) est linéaire, il existe une matrice \(M_f\) telle que :
\[ \boxed{\quad Y=M_f \cdot X \quad} \]
Comment déterminer \(M_f\) en connaissant \(f\), \(\mathcal{B}_n\) et \(\mathcal{B}_m\)
(Avec \(f\) linéaire)
Soient donc :
\[ \mathcal{B}_n = \left\{ \vec{e}_1, \vec{e}_2, ..., \vec{e}_n \right\} \quad\text{ une base de } \mathbb{R}^n \]
\[ \mathcal{B}_m = \left\{ \vec{v}_1, \vec{v}_2, ..., \vec{v}_m \right\} \quad\text{ une base de } \mathbb{R}^m \]
Soit également \(\vec{x} = x_1 \vec{e}_1 + x_2 \vec{e}_2 + ... + x_n \vec{e}_n\) un vecteur de \(\mathbb{R}^n\).
Puisque \(f\) est linéaire, on peut calculer :
\[ \begin{align*} \vec{y} &= f(\vec{x}) = f(x_1 \vec{e}_1 + x_2 \vec{e}_2 + ... + x_n \vec{e}_n)\\\\ &= x_1 f(\vec{e}_1) + x_2 f(\vec{e}_2) + ... + x_n f(\vec{e}_n)\\\\ &= \left( f(\vec{e}_1), f(\vec{e}_2) , ..., f(\vec{e}_n) \right)\cdot \begin{pmatrix} x_1\\x_2\\\vdots\\x_n\end{pmatrix} \end{align*} \]
Comme les \(f(\vec{e}_i)\) sont les images par \(f\) des vecteurs de a base \(\mathcal{B}_n\), ce sont des vecteurs de \(\mathbb{R}^m\). On doit donc les exprimer dans la base \(\mathcal{B}_m\).
Notons donc :
\[ f(\vec{e}_i) = \begin{pmatrix} f_{1i}\\f_{2i}\\\vdots\\f_{mi}\end{pmatrix} \]
On aura alors :
\[ \vec{y} = f(\vec{x}) = \begin{pmatrix}y_1\\y_2\\\vdots\\y_m\end{pmatrix} = \begin{pmatrix} f_{11} & ... & f_{1i} & ... & f_{1n}\\ f_{21} & ... & f_{2i} & ... & f_{2n}\\ \vdots && \vdots && \vdots\\ f_{m1} & ... & f_{mi} & ... & f_{mn} \end{pmatrix} \cdot \begin{pmatrix} x_1\\x_2\\\vdots\\x_n\end{pmatrix} \]
\[ \Rightarrow \quad \boxed{\quad Y = M_f \cdot X\quad} \]
Ceci montre qu’à une application linéaire \(f\), on peut associer une matrice \(M_f\) telle que :
\[ \text{Si } \space \vec{y} = f(\vec{x}) \quad \text{ alors } \quad Y=M_f \cdot X \]
De plus, on sait maintenant comment construire cette matrice \(M_f\). En effet, on voit que la ie colonne de \(M_f\) vaut simplement \(f(\vec{e}_i)\), c’est-à-dire l’image par \(f\) du ie vecteur de base.
On résume ceci dans le théorème suivant :
Soit \(f\) une application linéaire telle que :
\[ \begin{align*} f: \mathbb{R} ^n &\longmapsto \mathbb{R}^m\\ \vec{x}&\longmapsto \vec{y} = f(\vec{x}) \end{align*} \]
Soit également \(\mathcal{B}_n\), une base de \(\mathbb{R}^n\) et \(X\), la colonne des coordonnées de \(\vec{x}\) dans cette base \(\mathcal{B}_n\).
Soit encore \(\mathcal{B}_m\), une base de \(\mathbb{R}^m\) et \(Y\), la colonne des coordonnées de \(\vec{y}\) dans cette base \(\mathcal{B}_m\)
Alors on a :
\[ \boxed{Y=M_f \cdot X} \]
Et \(M_f\) est une matrice d’ordre \(m\times n\) dont les colonnes sont les images par \(f\) des vecteurs de la base \(\mathcal{B}_n\) exprimés dans la base \(\mathcal{B}_m\)
Soit une application linéaire \(f:\mathbb{R}^n \longmapsto \mathbb{R}^m\)
On définit l’image de \(f\), notée \(\mathcal{Im}(f)\), comme le sous-ensemble de \(\mathbb{R}^m\) constitué des vecteurs qui sont l’image par \(f\) d’au moins un vecteur de \(\mathbb{R}^m\).
Si \(M_f\) est la matrice associée à l’application \(f\), on parlera alors de l’image de \(M_f\), notée \(\mathcal{Im}(M_f)\) comme étant l’ensemble des \(Y\in \mathbb{R}^m\) qui sont images d’au moins un \(X\in \mathbb{R}^n\).
Soit l’application linéaire \(f:\mathbb{R}^n \longmapsto \mathbb{R}^m\)
On définit le noyau de \(f\), noté \(\mathcal{Ker}(f)\), comme le sous-ensemble des vecteurs de \(\mathbb{R}^n\) dont l’image est le vecteur nul de \(\mathbb{R}^m\).
Si \(M_f\) est la matrice associée à l’application \(f\), on parlera alors du noyau de \(M_f\), noté \(\mathcal{Ker}(M_f)\) comme étant l’ensemble des \(X\in\mathbb{R}^n\) qui ont pour image l’élément \(\vec{0}\) de \(\mathbb{R}^m\).
On a qu’un qu’un sous-espace de \(\mathbb{R}^n\) possède au maximum \(n\) vecteurs indépendants. De ce fait, on dira que \(\mathbb{R}^n\) est de dimension \(n\).
Une famille de \(m\) vecteurs indépendants de \(\mathbb{R}^n\) forme une base pour un sous-espace \(S\) de \(\mathbb{R}^n\). On a alors que \(\dim(S) = m\), où \(m\leq n\).
Soit l’application linéaire \(f : \mathbb{R}^n \longmapsto \mathbb{R}^m\).
On a alors que \(\mathcal{Ker}(f)\) est un sous-espace de \(\mathbb{R}^n\) et que \(\mathcal{Im}(f)\) est un sous-espace de \(\mathbb{R}^m\).
Ceci découle du fait que :
Ceci amène alors au théorème suivant :
Soit l’application linéaire \(f : \mathbb{R}^n \longmapsto \mathbb{R}^m\).
Alors on a que :
\[ n = \dim(\mathcal{Ker}(f)) + \dim(\mathcal{Im}(f)) \]
Soit \(f : A\longmapsto B\) une application de \(A\) dans \(B\).
\(f\) est injective si et seulement si \[ \forall x, y \in A, x\neq y \Rightarrow f(x) \neq f(y) \]
\(f\) est surjective si et seulement si \[ \forall x' \in B, \exists x\in A, x' =f(x) \]
\(f\) est bijective si et seulement si elle est à la fois surjective et injective.
Soit \(f:\mathbb{R}^n\longmapsto\mathbb{R}^m\) une application linéaire et soit \(M_f\) la matrice associée à \(f\).
Alors :
\(f\) est bijective si et seulement si les colonnes de \(M_f\) forment une base de \(\mathbb{R}^m\)
\(f\) est injective si et seulement si les colonnes de \(M_f\) sont indépendantes mais ne forment pas une base de \(\mathbb{R}^m\)
\(f\) est surjective si et seulement si les colonnes de \(M_f\) contiennent une base de \(\mathbb{R}^m\)
Un déterminant est une application telle que : \[ \begin{align*} \mathbb{R}^n\times \mathbb{R}^n \times ...\times \mathbb{R}^n &\longmapsto \mathbb{R}\\\\ \left( \vec{v}_1, \vec{v}_2, ..., \vec{v}_n \right) &\longmapsto d = \det(\vec{v}_1, \vec{v}_2,...,\vec{v}_n) \end{align*} \]
Un déterminant est une application qui associe à une famille de \(n\) vecteurs de \(\mathbb{R}^n\) une grandeur scalaire \(d\)
Le déterminant doit posséder les trois propriétés fondamentales suivantes :
Propriété 1 : \(d\) doit être multilinéaire, c.-à-d. linéaire p.r. à chacune de ses variables.
Propriété 2 : \(d\) doit être antisymétrique, c.-à-d. que le signe de \(d\) change quand on échange la position de deux de ses arguments.
Propriété 3 : \(d\) doit être normalisé, c.à-d. qu’il vaut 1 quand on l’applique à la base canonique de \(\mathbb{R}^n\).
Il n’existe qu’une seule et unique application qui satisfait ces trois propriétés.
Soit A une matrice \(n\times n\). A chaque éléments \(A_{ij}\) de \(A\) est associé un mineur noté \(\Delta_{ij}\) qui est définit comme le déterminant de \(\tilde{A}\), une matrice d’ordre \((n-1)\times(n-1)\) obtenue à partir de \(A\), en supprimant la ie ligne et je colonne.
On va calculer le déterminant d’une matrice \(n\times n\) à partir des déterminant de plusieurs matrices d’ordre \((n-1)\times (n-1)\) lesquels se calculeront à leur tour à partir de déterminant de matrices d’ordre \((n-2)\times (n-2)\) et ainsi de suite!
Au final, il n’y aura plus que des déterminant de matrices d’ordre \(2\times 2\) à calculer.
Définition 1
Le déterminant d’une matrice \(A\) d’ordre \(2\times 2\) est défini par \[ \boxed{\det (A_{2\times 2}) = \det\begin{pmatrix}a&b\\c&d\end{pmatrix} = ad-cb} \]
Définition 2
Le déterminant d’une matrice \(A\) d’ordre \(n\times n\) s’obtient par un développement relativement à l’une de ses colonne ou l’une de ses lignes. \[ \boxed{\det (A_{n\times n}) = \sum_{i=1}^n (-1)^{i+j} \cdot a_{ij}\cdot\Delta_{ij}} \]
Soit \(A\) une matrice d’ordre \(n\times n\). On note alors \(\vec{c}_i\) les colonnes de \(A\) et \(\vec{\ell}_i\) ses lignes.
Le déterminant \(\det A\) a les propriétés suivantes :
La permutation de deux lignes ou deux colonnes quelconques de \(A\) change le signe du déterminant.
Si \(A\) contient deux colonnes ou lignes identiques, alors \(\det A=0\).
Ajouter un multiple d’une colonne à une autre colonne ne change pas le déterminant (idem pour les lignes).
Le déterminant de \(A\) est différent de zéro si et seulement si les colonnes (ou les lignes) de \(A\) forment une base de \(\mathbb{R}^n\).
Le déterminant de \(A\) et celui de sa transposée \(A^t\) sont identiques.
Le déterminant du produit est égal au produit des déterminants.
Le déterminant d’une matrice et celui de son inverse sont l’inverse l’une de l’autre.
Définition 1
\(A^{-1}\) est l’inverse de \(A\) si et seulement si
\[ \boxed{A^{-1} \cdot A = A\cdot A^{-1} = \mathbb{1}} \]
Définition 2
\(A\) est singulière si \(\det A=0\)
\(A\) est régulière si \(\det A \neq 0\)
Théorème de base
\(A\) est inversible si et seulement si son déterminant est non-nul :
\[ \boxed{A^{-1} \mbox{ existe } \space \Leftrightarrow \space \det A \neq 0} \]
\[ \boxed{\det(A^{-1}) = \frac{1}{\det A}} \]
\[ \boxed{(A\cdot B)^{-1} = B^{-1}\cdot A^{-1}} \]
\[ \boxed{(A^t)^{-1} = (A^{-1})^t} \]
\[ \boxed{(\lambda A)^{-1} = \frac{1}{\lambda}A^{-1}} \]
Il est possible d’inverser une matrice en résolvant le système de \(n^2\) équations à \(n^2\) inconnues : \(A\cdot A^{-1}=\mathbb{1}\).
Il est également possible d’inverser une matrice avec la méthode suivante :
L’inverse de \(A\) est la transposée de la matrice des cofacteurs, divisée par le déterminant de \(A\).
La matrice des cofacteurs est dite comatrice. Elle est notée \(\mathrm{com}(A)\) et elle est définie par :
\[ \mathrm{com}(A)_{ij} = (-1)^{i+j} \cdot \Delta _{ij} \]
Ainsi, \(A^{-1}\) est donnée par :
\[ \boxed{A^{-1} = \frac{1}{\det A}\cdot\left( \mathrm{com}(A) \right)^t} \]
Soit \(\mathcal{B} = \{ \vec{e}_1, \vec{e}_2, \vec{e}_3 \}\) une base de \(\mathbb{R}^3\) (nommée ancienne base).
Soit \(\mathcal{B}' = \{ \vec{u}_1, \vec{u}_2 , \vec{u}_3\}\) une autre base de \(\mathbb{R}^3\) (nommée nouvelle base).
Pour tout vecteur, il est possible d’exprimer \(\vec{u}_1, \vec{u}_2, \vec{u}_3\) comme combinaison linéaire des vecteurs \(\vec{e}_1, \vec{e}_2, \vec{e}_3\). On dira que nous exprimons les vecteurs de la nouvelle base \(\mathcal{B}'\) à l’aide des vecteurs de l’ancienne base \(\mathcal{B}\).
\[ \begin{align*} \vec{u}_1 &= \alpha_1 \vec{e}_1 + \alpha_2 \vec{e}_2 + \alpha_3 \vec{e}_3\\\\ \vec{u}_2 &= \beta_1 \vec{e}_1 + \beta_2 \vec{e}_2 + \beta_3 \vec{e}_3\\\\ \vec{u}_3 &= \gamma_1 \vec{e}_1 + \gamma_2 \vec{e}_2 + \gamma_3 \vec{e}_3 \end{align*} \]
On forme alors la matrice \(P\) en écrivant en colonne les composantes de nouveaux vecteurs de base dans l’ancienne base :
\[ P = \begin{pmatrix}\alpha_1&\beta_1&\gamma_1\\\alpha_2&\beta_2&\gamma_2\\\alpha_3&\beta_3&\gamma_3 \end{pmatrix} \]
\(P\) est appelée la matrice de passage de la base \(\mathcal{B}\) à la base \(\mathcal{B'}\).
Il est alors clair que :
\[ (\mathcal{B'}) = (\mathcal{B})\cdot P \]
Considérons un vecteur \(\vec{x}\) de \(\mathbb{R}^3\).
Soit \(X = \begin{pmatrix} x_1\\x_2\\x_3\end{pmatrix}\) la colonne des composantes de \(\vec{x}\) dans \(\mathcal{B}\). On a alors :
\[ \vec{x} = x_1 \vec{e}_1 + x_2\vec{e}_2 + x_2\vec{e}_3 = (\vec{e}_1, \vec{e}_2, \vec{e}_3)\cdot \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix} = (\mathcal{B}) \cdot X \]
Le même vecteur \(\vec{x}\) peut également s’exprimer dans la base \(\mathcal{B'}\). On aura alors :
\[ \vec{x} = x'_1 \vec{u}_1 + x'_2 \vec{u}_2 + x'_3 \vec{u}_3 = (\vec{u}_1, \vec{u}_2, \vec{u}_3)\cdot \begin{pmatrix}x'_1\\x'_2\\x'_3\end{pmatrix} = (\mathcal{B'}) \cdot X' \]
On en déduit alors que :
\[ (\mathcal{B})\cdot X = (\mathcal{B'})\cdot X' \]
Or, \((\mathcal{B'}) = (\mathcal{B})\cdot P\), ainsi :
\[ (\mathcal{B})\cdot X = (\mathcal{B}) \cdot P \cdot X' \]
D’où on en tire les relations entre \(X\) et \(X'\) :
\[ \boxed{X = P \cdot X'} \]
\[ \boxed{X' = P^{-1} \cdot X} \]
Attention :
\[ (\mathcal{B'}) = (\mathcal{B})\cdot P \]
MAIS
\[ X = P\cdot X' \]
et donc
\[ X' = P^{-1} \cdot X \]
Considérons l’application linéaire suivante :
\[ \begin{align*} f: \mathbb{R}^3 &\longmapsto \mathbb{R}^3\\ \vec{x}&\longmapsto \vec{y} = f(\vec{x}) \end{align*} \]
ainsi que deux bases \(\mathcal{B}\) et \(\mathcal{B'}\) de \(\mathbb{R}^3\).
On a alors que :
\[ Y=M\cdot X \quad \mbox{ et }\quad Y' = M'\cdot X' \]
Or, en connaissant \(\mathcal{B}\) et \(\mathcal{B'}\), on connaît la matrice de passage \(P\), et ainsi :
\[ X = P\cdot X' \quad \mbox{ et } \quad Y=P\cdot Y' \]
Et donc :
\[ \begin{align*} &P \cdot Y' = M \cdot P \cdot X'\\\\ \Leftrightarrow \quad & Y' = P^{-1}\cdot M\cdot P\cdot X'\\\\ \Leftrightarrow \quad & Y' = M' \cdot X' \end{align*} \]
Finalement, on peut poser que :
\[ \boxed{M' = P^{-1}\cdot M \cdot P} \]
Soient donc
\[ \vec{y} = f(\vec{x}) \left\{ \begin{array}{ll} Y = MX & \mbox{Dans la base } \mathcal{B}\\Y' = M'X'& \mbox{Dans la base } \mathcal{B'}\end{array}\right. \]
et la matrice de passage \(P\) telle que :
\[ \left\{ \begin{array}{l} X= PX'\\Y=PY' \end{array} \right. \]
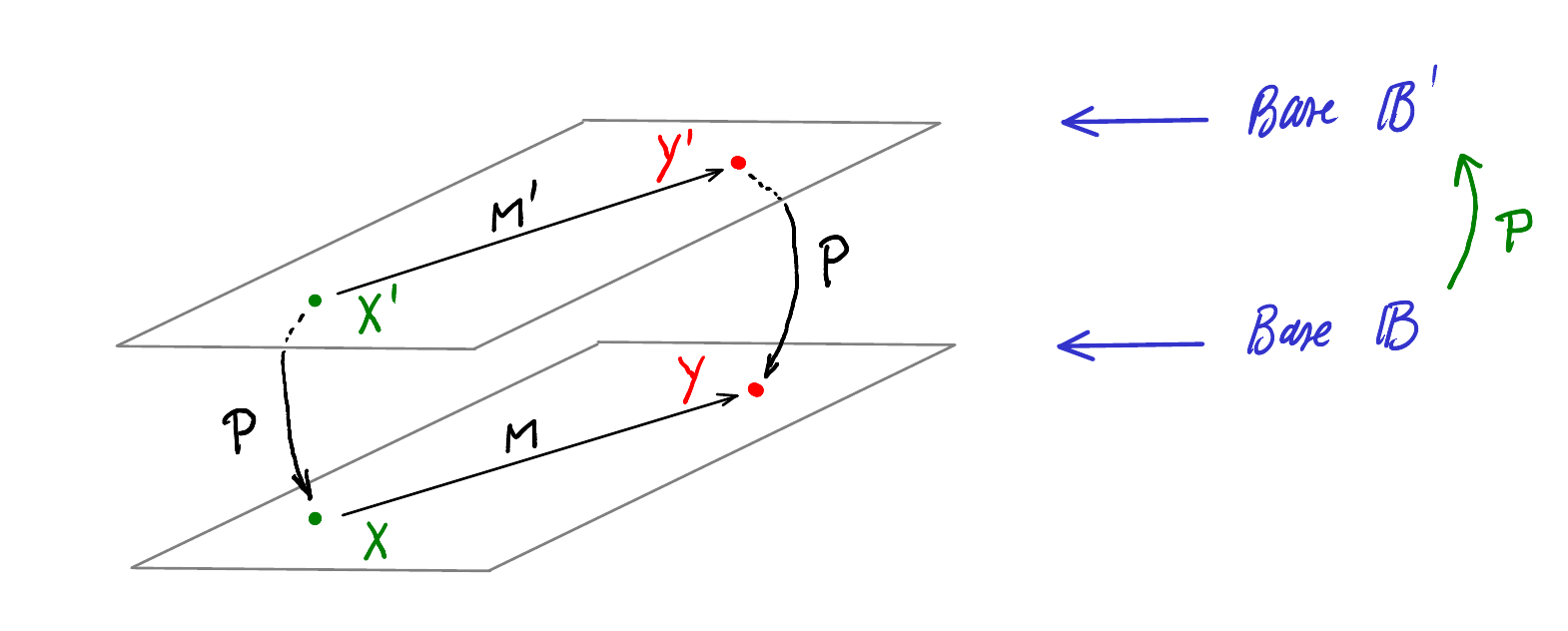
Ce diagramme représente symboliquement les relation ci-dessus :

On peut ainsi visualiser directement les chemins entre \(X, X', Y\) et \(Y'\).
Par exemple, On voit que \(Y' = \textcolor{blue}{M'} X'\) mais aussi \(Y'=\textcolor{blue}{P^{-1}MP}X'\), ainsi on en déduit que \(M'=P^{-1}MP\).
Dans le cas d’une application linéaire de \(\mathbb{R}^n\longmapsto\mathbb{R}^m\), il est évident qu’il n’est pas possible d’utiliser la même base pour l’espace de départ et d’arrivée.
Considérons \(f:\mathbb{R}^3 \longmapsto\mathbb{R}^2\) et introduisons :
\[ \begin{array}{ll} \mathcal{B}_3 : & \text{Une base de $\mathbb{R}^3$}\\ \mathcal{B}_2 : & \text{Une base de $\mathbb{R}^2$}\\ M_f : & \text{La matrice $f$ dans ces deux bases} \end{array} \]
Nous avons alors :
\[ Y = M_f X \quad\text{avec}\quad\begin{array}{l}Y\in\mathbb{R}^2 \text{ composantes de $y$ dans la base } \mathcal{B}_2\\X\in\mathbb{R}^3 \text{ composantes de $x$ dans la base }\mathcal{B}_3\end{array} \]
\(M_f\) dépend bien-sûr des bases \(\mathcal{B}_2\) et \(\mathcal{B}_3\).
Introduisons maintenant :
\[ \begin{array}{l}\mathcal{B}'_3:&\text{ Une nouvelle base de }\mathbb{R}^3\\\mathcal{B}'_2:&\text{ Une nouvelle base de }\mathbb{R}^2\\M'_f:&\text{ La matrice de $f$ dans ces deux bases}\end{array} \]
Nous aurons :
\[ Y' = M'_f X' \quad\text{avec}\quad\begin{array}{l}Y'\in\mathbb{R}^2 \text{ composantes de $y$ dans la base } \mathcal{B}'_2\\X'\in\mathbb{R}^3 \text{ composantes de $x$ dans la base }\mathcal{B}'_3\end{array} \]
Et la matrice \(M'_f\) dépend des bases \(\mathcal{B}'_2\) et \(\mathcal{B}'_3\).
En connaissant \(\mathcal{B}_2,\mathcal{B}_3,\mathcal{B}'_2,\mathcal{B}'_3\) on souhaite exprimer \(M'_f\) à partir de \(M_f\) et vice-versa.
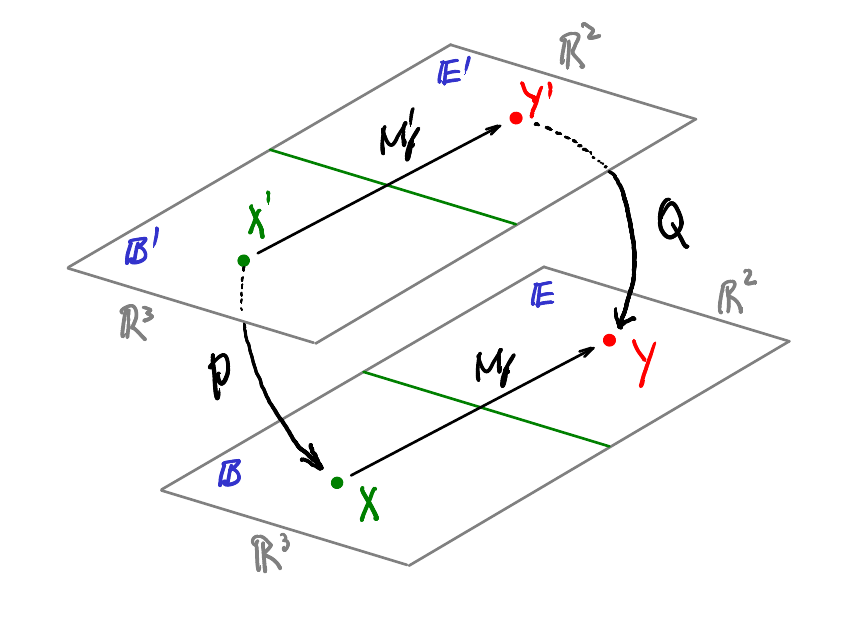
Ainsi :
\[ X=PX'\quad\mbox{ et }\quad Y=QY' \]
Mais aussi
\[ Y' = M'_fX' \]
\[ Y' = Q^{-1}M_fPX' \]
D’où la relation que nous cherchons :
\[ \boxed{M'_f = Q^{-1}M_fP} \]
\[ \boxed{M_f = QM'_fP^{-1}} \]
La forme générale d’un système de \(n\) équations linéaire \(n\) inconnues est de la forme \[ \left\{ \begin{array}{l} a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n = b_1\\ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n = b_2\\ \cdots\\ a_{n1}x_1 + a_{n2}x_2 + ... + a_{nn}x_n = b_n \end{array} \right. \] Ce système peut être écrit sous forme matricielle : \[ \begin{pmatrix}a_{11}&a_{12}& \cdots & a_{1n}\\a_{21}& a_{22} & \cdots& a_{2n}\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn} \end{pmatrix}\cdot \begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix} = \begin{pmatrix} b_1\\b_2\\\vdots\\b_n \end{pmatrix} \] On a alors l’équation matricielle : \[ \boxed{A\cdot X = B} \] Ainsi, écrit sous forme matricielle, un système d’équations apparaît comme une application linéaire de matrice \(A\) qui transforme un vecteur inconnu \(X\) vers un vecteur donnée \(B\).
Résoudre un système d’équations linéaires consiste donc à trouver tous les éléments \(X\) de l’espace de départ qui sont envoyés sur le vecteur \(B\) par l’équation linéaire associée à la matrice \(A\).
On peut distinguer deux cas distincts :
L’application est donc bijective (=> \(A\) inversible) c-à-d surjective (=> Il existe forcément une solution) et injective (=> cette solution est unique).
Cela implique que : \[ \mathcal{Im} (A) = \mathbb{R}^n,\quad \mathcal{Ker}(A) = \vec{0} \]
\[ \dim(\mathcal{Im}(A)) = n, \quad \dim(\mathcal{Ker}(A)) = 0 \]
Les colonnes ne sont pas pas indépendantes ! (\(\Rightarrow \det(A)=0\))
On peut distinguer deux cas :
Si \(B\not\in \mathcal{Im}(A)\), il est impossible de trouver \(X\) t.q. \(AX=B\)
Le système n’a donc pas de solutions.
Si \(B\in\mathcal{Im}(A)\), il y a forcément une solution.
On cherche maintenant à savoir s’il existe une ou plusieurs solutions.
Considérons \(X_p\), une solution particulière du système. Ainsi,
\[ AX_p = B \]
Ajoutons à \(X_p\) le vecteur \(k_i\in\mathcal{Ker}(A)\). Nous avons alors \(X=X_p+k_i\).
Il est très simple de vérifier que \(X\) est également une solution.
En effet :
\[ AX = A(X_p+k_i) = AX_p + \underbrace{Ak_i}_{\vec{0}} = B \]
Comme \(\dim(\mathcal{Ker}(A))>0\), alors il existe une infinité d’éléments \(k_i\in\mathcal{Ker}(A)\) et donc une infinité de solutions \(X=X_p+k_i\).
Un système de \(n\) équations linéaires à \(n\) inconnues s’écrit \(AX=B\)
Si \(\det(A)\neq 0\), il existe une unique solution \(X\)
Le système est dit régulier.
Si \(\det(A)=0\) :
Il n’existe pas de solution si \(B\not\in\mathcal{Im}(A)\)
Il existe une infinité de solution \(X=X_p + k_i, \space k_i\in\mathcal{Ker}(A)\) si \(B\in\mathcal{Im}(A)\).
Le système est dit singulier.
Le système d’équations \(AX=B\) possède \(n\) équations à \(n\) inconnues. La matrice \(A\) est donc carrée, d’ordre \(n\times n\).
De plus, on considère ici les systèmes réguliers, ainsi, \(\det(A) \neq 0\) ; \(A\) est donc inversible.
On a alors : \[ \begin{align*} &AX=B\\\\\Leftrightarrow\quad& \underbrace{A^{-1}A}_{\mathbb{1}}X = A^{-1}B\\\\\Leftrightarrow\quad&\boxed{X=A^{-1}B} \end{align*} \]
Soit \(MX=B\) un système d’équation t.q. \(\det(B)\neq 0\).
Soit également \(\vec{c}_i\) les colonnes de \(M\), donc \(M=(\vec{c}_1,\vec{c}_2, ..., \vec{c}_n)\).
Alors, \(x_i\), la ie composante de \(X\) est donnée par : \[ \boxed{x_i = \frac{\det(\vec{c}_1, \vec{c}_2, ...,\overbrace{B}^{\text{$\vec{c}_i$ devient $B$}},...,\vec{c}_n)}{\det(\vec{c}_1,\vec{c}_2, ...,\vec{c}_i,...,\vec{c}_n)}} \] L’avantage de cette méthode est qu’on peut déterminer la ie inconnue sans en déterminer les autres si elles ne nous intéressent pas.
\(\text{\textcolor{RED}{[A COMPLETER]}}\)
Exported with pandoc 2.9.2.1 on Fri Jun 24 2022 at 17:35:22 CEST. @ylked
All informations are given without warranty. All rights reserved ©