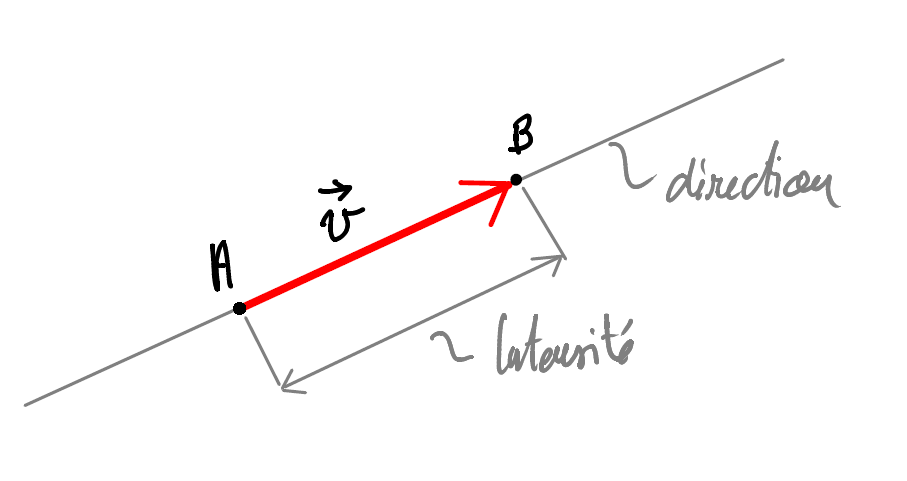
Les grandeurs scalaires peuvent être entièrement représentées par un nombre réel. Les grandeurs vectorielles, ne sont pas seulement définies par un nombre réel, appelé intensité, mais aussi par une direction et un sens.
C’est pour ça que les grandeurs vectorielles sont représentées par des vecteurs.
Un vecteur est définir par
Il est alors naturel de représenter un vecteur par une flèche.

On note souvent \(\vec{u} = \overrightarrow{AB}\)
| nom | notation | description |
|---|---|---|
| vecteur nul | \(\vec{0}\) | vecteur de norme nulle |
| vecteur unité | \(\vec{u}\) | vecteur de norme \(\|\vec{u}\|=1\) |
| vecteur égaux | \(\vec{a}=\vec{b}\) | vecteurs dont la norme, le sens et la direction sont égaux |
| vecteur opposés | \(\vec{a}\) et \(-\vec{a}\) | vecteurs dont la norme et la direction sont les mêmes et le sens est opposé. |
| Norme | \(\|\vec{a}\|\) | longueur du vecteur (aussi appelé module ou intensité) |
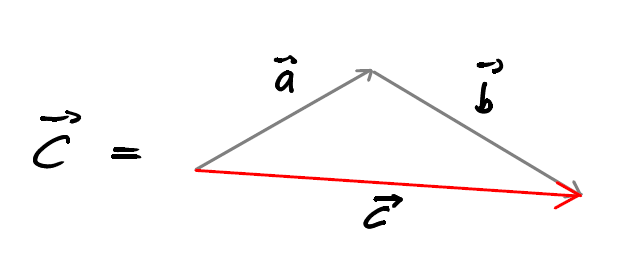
\[ \boxed{ \quad \vec{c} = \vec{a} + \vec{b} \quad} \]
L’addition vectorielle s’obtient en mettant \(\vec{a}\) et \(\vec{b}\) bout à bout.
L’addition de deux vecteurs donne toujours un vecteur.
Il n’est pas possible d’additionner un vecteur avec un scalaire.
\[ \boxed{ \quad \vec{c} = \vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \quad} \]
La soustraction d’un vecteur consiste à l’addition de son opposé.
\[ \begin{array}{lll} 1. & \vec{a} + \vec{b} = \vec{b} + \vec{a} & \quad\text{: Commutativité}\\ 2. & (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) & \quad\text{: Associativité}\\ 3. & \vec{a} + \vec{0} = \vec{a} & \quad : \vec{0} \text{ est l'élément neutre} \\ 4. & \vec{a} + (-\vec{a}) = \vec{0}, \quad \forall \vec{a} & \quad\text{: Tout vecteur a un opposé}\\ 5. & \|\vec{a} + \vec{b}\| \leq \|\vec{a}\| + \|\vec{b}\| & \quad \text{: Inégalité triangulaire} \end{array} \]
Soit \(\vec{u}\) un vecteur et \(\alpha\) un scalaire.
\(\vec{u}' = \alpha \cdot \vec{u}\) est un nouveau vecteur tel que :
Par ailleurs, en multipliant tout vecteur \(\vec{u}\) par l’inverse de sa norme, on obtient un vecteur unitaire dont le sens et la direction sont les mêmes que celle du vecteur \(\vec{u}\).
\[ \begin{align*} &\|\vec{u}\| \neq 1 \\\\ &\vec{v} = \frac{1}{\|\vec{u}\|} \cdot \vec{u} = \frac{\vec{u}}{\|\vec{u}\|} \\\\ \Rightarrow \quad& \|\vec{v}\| = 1 \end{align*} \]
\[ \begin{array}{lll} 1. & \alpha \cdot \vec{u} = \vec{u} \cdot \alpha & \quad\text{: Commutativité} \\\\ 2. & \mu \cdot (\alpha \cdot \vec{u}) = \alpha \cdot (\mu \cdot \vec{u}) & \quad\text{: Associativité}\\\\ 3. & (\alpha + \mu) \cdot \vec{u} = \alpha \cdot \vec{u} + \mu \cdot \vec{u} & \quad\text{: Distributivité des scalaires} \\\\ 4. & \alpha(\vec{u} + \vec{v}) = \alpha \cdot \vec{u} + \alpha \cdot \vec{v} & \quad\text{: Distributivité des vecteurs} \\\\ \end{array} \]
Soit \(\vec{a}\) et \(\vec{b}\) deux vecteurs non-nuls du plan.
On appelle combinaison linéaire de \(\vec{a}\) et \(\vec{b}\) un vecteur \(\vec{u}\) de la forme :
\[ \boxed{ \quad \vec{u} = \alpha \cdot \vec{a} + \beta \cdot \vec{b} \quad} \]
On dit que \(\vec{a}\) et \(\vec{b}\) sont indépendant s’ils ne sont pas colinéaires.
Autrement dit :
\[ \boxed{ \quad \vec{b} \neq \lambda \vec{a}, \quad \forall \lambda \in \mathbb{R} \quad} \]
Ou encore :
\[ \boxed{ \quad \alpha \cdot \vec{a} + \beta \cdot \vec{b} = \vec{0} \quad \Leftrightarrow \quad \alpha = \beta = 0 \quad} \]
Pour la deuxième équivalence, cela signifie que deux vecteurs sont indépendants si et seulement si la seule et unique manière d’obtenir le vecteur nul est de prendre les valeurs zéro pour \(\alpha\) et \(\beta\).
Si \(\vec{a}\) et \(\vec{b}\) sont indépendants, ils forment alors une base du plan.
Cela signifie que tous les autres vecteurs du plan peuvent s’écrire comme une combinaison linéaire de \(\vec{a}\) et \(\vec{b}\).
Il existe de toute évidence une infinité de bases du plan !
On peut alors les classer selon 3 groupes :
\(\vec{e}_1 \perp \vec{e}_2\)
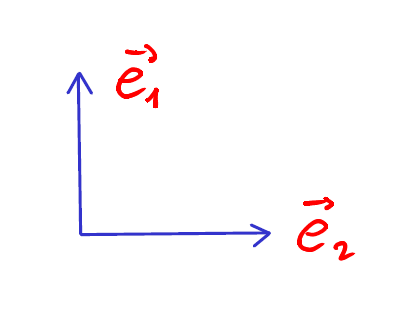
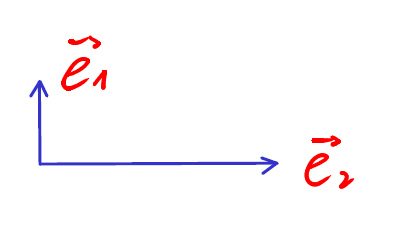
\(\vec{e}_1 \perp \vec{e}_2\) et \(\|\vec{e}_1\| = \|\vec{e}_2\| = 1\)
De plus, on la définition suivante :
On appelle base canonique, une base orthonormée dont l’angle orienté menant de \(\vec{e} _1\) à \(\vec{e} _2\) vaut \(+\frac{\pi}{2}\).
Soient :
Alors : Les nombres \(\alpha\) et \(\beta\) sont les composantes de \(\vec{w}\) dans la base \(\left\{ \vec{a} , \vec{b} \right\}\)
Quand on travaille dans une base \(\left\{ \vec{a} , \vec{b} \right\}\) de \(\mathbb{R}^2\) bien définie, les données des composantes d’un vecteur est suffisante pour complétement déterminer ce vecteur.
On prend alors l’habitude de noter :
\[ \boxed{ \quad \vec{w} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}_\mathcal{B_1} = \alpha \cdot \vec{a} + \beta \cdot \vec{b} \quad} \]
\(\begin{pmatrix}\alpha \\ \beta\end{pmatrix}_{\mathcal{B_1}}\) sont alors les composantes de \(\vec{w}\) dans la base \(\mathcal{B}_1\)
Il est fondamental de remarquer que :
On peut omettre d’indiquer la base quand le contexte permet de la connaitre sans ambiguïté ou qu’elle est orthonormée.
Dans un espace \(\mathcal{E}\) de \(\mathbb{R}^3\), deux vecteur \(\vec{a}\) et \(\vec{b}\) non-nuls et indépendants sont forcément coplanaires.
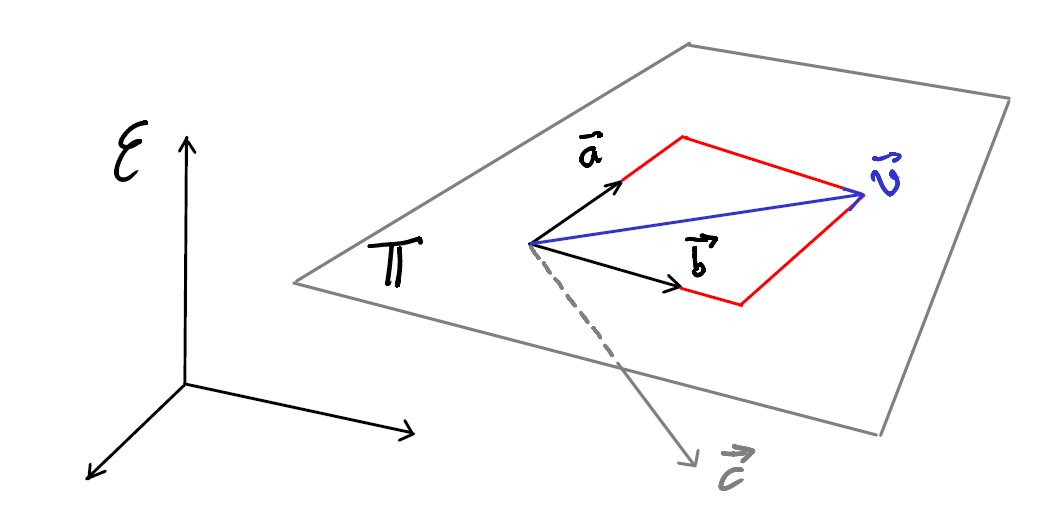
Si on ajoute un troisième vecteur \(\vec{c}\), on a deux possibilités :
Dans ce dernier cas, on dit que \(\vec{a}\), \(\vec{b}\) et \(\vec{c}\) sont linéairement indépendants et il forment une base de l’espace \(\mathcal{E}\). Tout autre vecteur \(\vec{w}\) de \(\mathcal{E}\) peut s ’écrire comme une combinaison linéaire de \(\vec{a}\), \(\vec{b}\) et \(\vec{c}\).
\[ \boxed{ \quad \vec{w} = \alpha \cdot \vec{a} + \beta \cdot \vec{b} + \gamma \cdot \vec{c} \quad} \]
\(\alpha\), \(\beta\) et \(\gamma\) sont les composantes de \(\vec{w}\) dans la base \(\left\{ \vec{a} , \vec{b} , \vec{c}\right\}\) .
Pour décrire les positions des points du plan, on introduit un repère :
Un repère dans le plan ou dans l’espace est formé d’un point de référence \(\mathcal{O}\) (l’origine) et d’une base de vecteurs.
Un repère détermine un système d’axes dans lequel la position de tout point est données par ses coordonnées.
Un repère est le couple \((\mathcal{O},\left\{ \vec{e}_1 , \vec{e}_2 \right\})\)
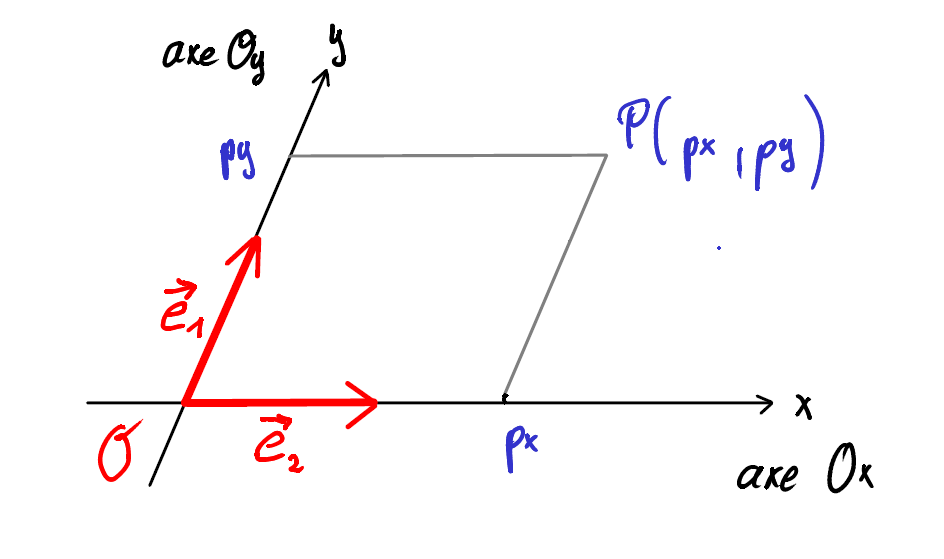
\(p_x\) et \(p_y\) sont les coordonnées de \(P\).
Un repère est le couple \((\mathcal{O},\left\{ \vec{e}_1 , \vec{e}_2,\vec{e}_3 \right\})\) qui définit trois axes :
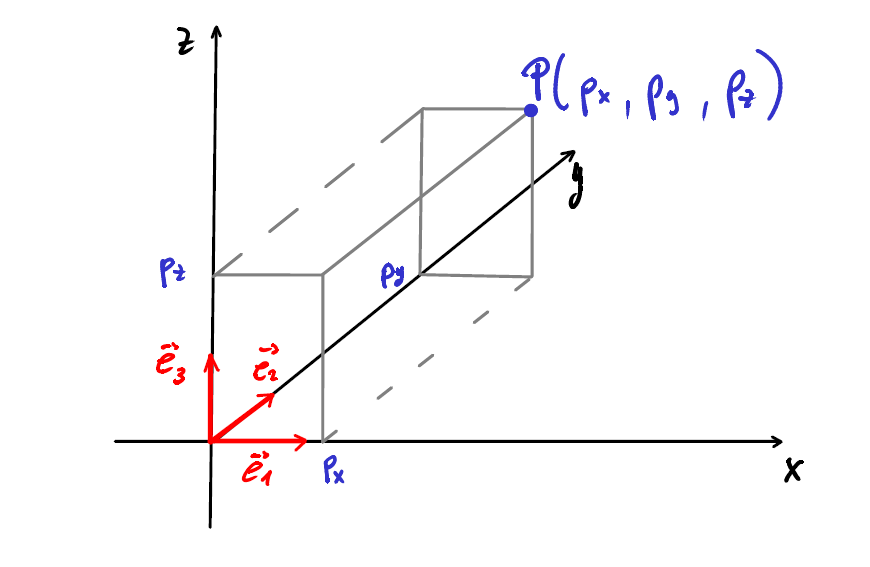
\(p_x\), \(p_y\) et \(p_z\) sont les coordonnées du point \(P\) dans le repère \((\mathcal{O},\left\{ \vec{e}_1 , \vec{e}_2,\vec{e}_3 \right\})\).
Attention : l’orientation des vecteurs est importante !
Par définition, la base canonique de \(\mathcal{E}\) est celle qui obéit à la “règle du tire-bouchon”.
On prend deux vecteurs orthonormés \(\vec{i}, \vec{j}\) et on fait tourner \(\vec{i}\) sur \(\vec{j}\) et on observe dans quel sens se dirigerait une visse qu’on tournerait dans ce sens.
Soit dans un repère, un point \(A\). On appelle le rayon vecteur du point \(A\) le vecteur \(\overrightarrow{OA}\).
Les composantes du rayon vecteur \(\overrightarrow{OA}\) sont les coordonnées du point \(A\).
\[ \overrightarrow{OA} = x_A \cdot \vec{e} _1 + y_A \cdot \vec{e} _2 = \begin{pmatrix} x_A\\y_A \end{pmatrix} \]
Soit alors un vecteur \(\overrightarrow{AB}\) dont l’origine est le point \(A\) et l’extrémité est le point \(B\). On peut exprimer le vecteur \(\overrightarrow{AB}\) à l’aide des vecteurs \(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) :
\[ \boxed{ \quad \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} \quad} \]
Preuve :
\[ \begin{align*} & \overrightarrow{OA} + \overrightarrow{AB} + \overrightarrow{BO} = \vec{0} \\\\ \Leftrightarrow \quad& \overrightarrow{OA} + \overrightarrow{AB}-\overrightarrow{OB} = \vec{0} \\\\ \Leftrightarrow \quad & \overrightarrow{OA}+\overrightarrow{AB} = \overrightarrow{OB}\\\\ \Leftrightarrow \quad & \overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA} \quad\Box \end{align*} \]
Les opérations vectorielles du paragraphe 3.1.3 peuvent également être effectuées en composantes.
Soient \(\vec{a}\) et \(\vec{b}\) deux vecteurs exprimés en composantes :
\[ \vec{a} = \begin{pmatrix} a_x\\a_y\\a_z \end{pmatrix} \quad \text{ et } \quad \vec{b} = \begin{pmatrix} b_x\\b_y\\b_z \end{pmatrix} \]
\[ \vec{a} + \vec{b} = \begin{pmatrix} a_x\\a_y\\a_z \end{pmatrix} + \begin{pmatrix} b_x\\b_y\\b_z \end{pmatrix} = \begin{pmatrix} a_x + b_x\\a_y+b_y\\a_z+b_z \end{pmatrix} \]
\[ \lambda \cdot \vec{a} = \lambda \cdot \begin{pmatrix} a_x\\a_y\\a_z \end{pmatrix} = \begin{pmatrix} \lambda \cdot a_x\\\lambda \cdot a_y \\ \lambda \cdot a_z \end{pmatrix} \quad,\space \lambda \in \mathbb{R} \]
\[ \vec{a} = \vec{b} \quad \Leftrightarrow \quad \begin{pmatrix}a_x\\a_y\\a_z\end{pmatrix} = \begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} \quad \Leftrightarrow \quad \left\{ \quad \begin{array}{} a_x = b_x\\a_y=b_y\\a_z=b_z \end{array} \right. \]
\[ \vec{0} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} \]
On peut additionner et soustraire des vecteurs entre eux ainsi que les multiplier par un scalaire. En revanche, la multiplication entre deux vecteur n’a pas de signification géométrique !
On introduit plutôt une opération nommée produit scalaire qui à deux vecteurs fait correspondre un scalaire tel que :
\[ \boxed{ \quad \vec{a} \cdot \vec{b} = \|\vec{a} \| \cdot \|\vec{b} \| \cdot \cos\theta \quad} \]
Où \(\theta\) est l’angle entre les deux vecteurs $ $ et \(\vec{b}\).
\[ \begin{array}{ll} 1. \quad & \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \\\\ 2. \quad & \lambda \cdot (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (\lambda \cdot \vec{b}) = (\lambda \cdot \vec{a}) \cdot \vec{b} \\\\ 3. \quad & \vec{a} \cdot \vec{b} = 0 \quad \Leftrightarrow \quad \vec{a} \perp \vec{b} \\\\ 4. \quad & \vec{a} \cdot \vec{a} = \|\vec{a} \| ^2 \quad \text{ et } \quad\vec{a} \cdot \vec{a} = 0 \quad\Rightarrow \quad\vec{a} = \vec{0} \\\\ 5. \quad& \vert{\vec{a} \cdot \vec{b}}\vert \leq \|\vec{a} \| \cdot \|\vec{b}\| \\\\ 6. \quad& \vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \end{array} \]
Preuve du point 6. :
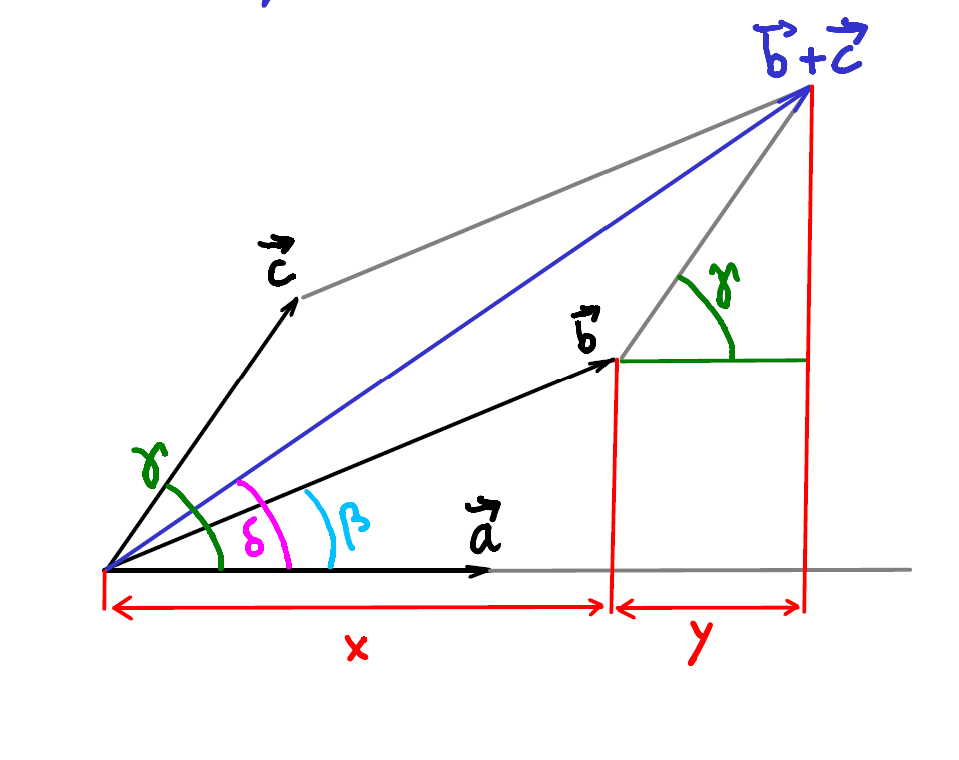
\[ \begin{align*} & \vec{a} \cdot (\vec{b} + \vec{c}) = \|\vec{b} + \vec{c} \| \cdot \|\vec{a} \| \cdot \cos\delta \space \\&\text{ avec } \quad \|\vec{b} + \vec{c} \| = x + y \\\\ \Rightarrow \quad& \vec{a} \cdot (\vec{b} + \vec{c}) = \|\vec{a} \| \cdot (x+y) = \|\vec{a}\| \cdot x + \|\vec{a} \| \cdot y\\\\ &\text{On sait aussi que } \left\{ \begin{array}{ll} x= \|\vec{b} \| \cdot \cos\beta \\y= \|\vec{c} \| \cdot \cos\gamma \end{array} \right. \\\\ \Rightarrow \quad & \vec{a} \cdot (\vec{b} + \vec{c}) = \underbrace{\|\vec{a} \| \cdot \|\vec{b} \| \cdot \cos\beta }_{\vec{a} \cdot \vec{b} } + \underbrace{\|\vec{a} \| \cdot \|\vec{c} \| \cdot \cos\gamma }_{\vec{a} \cdot \vec{c} } \\\\ \Rightarrow \quad & \vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} \quad \Box \end{align*} \]
Soit le repère orthonormé \((\mathcal{O}, \{ \vec{e} _1, \vec{e} _2\})\). Soient aussi deux vecteurs \(\vec{a}\) et \(\vec{b}\) dont on connait les composantes dans ce repère :
\[ \begin{align*} & \vec{a} = a_1 \cdot \vec{e} _1 + a_2 \cdot \vec{e} _2 = \begin{pmatrix}a_1\\a_2\end{pmatrix} \\\\ & \vec{b} = b_1 \cdot \vec{e} _1 + b_2 \cdot \vec{e} _2 = \begin{pmatrix}b_1\\b_2\end{pmatrix} \end{align*} \]
On calcule alors le produit scalaire \(\vec{a} \cdot \vec{b}\) en utilisant les propriétés 2. et 6. :
\[ \begin{align*} \vec{a} \cdot \vec{b} &= (a_1 \vec{e} _1 + a_2 \vec{e} _2) \cdot (b_1 \vec{e} _1 + b_2 \vec{e} _2) \\\\ &= (a_1 \vec{e} _1 + a_2 \vec{e} _2) \cdot b_1 \vec{e} _1 + (a_1 \vec{e} _1 + a_2 \vec{e} _2) \cdot b_2 \vec{e} _2 \\\\ &= a_1 \vec{e} _1 \cdot b_1 \vec{e} _1 + a_2 \vec{e} _2 \cdot b_1 \vec{e} _1 + a_1 \vec{e} _1 \cdot b_2 \vec{e} _2 + a_2 \vec{e} _2 \cdot b_2 \vec{e} _2 \\\\ &= a_1 b_1 \cdot (\vec{e} _1 \cdot \vec{e} _1 )+ a_2 b_1 \cdot (\vec{e} _1 \cdot \vec{e} _2) + a_1 b_2 \cdot (\vec{e} _2 \cdot \vec{e} _1) + a_2 b_2 \cdot (\vec{e} _2 \cdot \vec{e} _2) \end{align*} \]
Or, on sait que \(\vec{e} _1 \perp \vec{e} _2\) :
\[ \left\{ \begin{array}{ll} \vec{e} _1 \cdot \vec{e} _1 = 1 \\ \vec{e}_1 \cdot \vec{e} _2 = \vec{e} _2 \cdot \vec{e} _1 = 0 \\ \vec{e} _2 \cdot \vec{e} _2 = 1 \end{array} \right. \]
Dans un repère orthonormé (uniquement !) on a donc le résultat suivant :
\[ \boxed{ \quad \vec{a} \cdot \vec{b} = a_1 \cdot b_1 + a_2 \cdot b_2 \quad} \]
Ce résultat se généralise dans un espace à \(n\) dimensions avec un repère orthonormé :
\[ \boxed{ \quad \vec{a} \cdot \vec{b} = \sum_{i=1, j=1}^n {a_i b_j} \cdot (\vec{e} _i \cdot \vec{e} _j) = \sum_{i=1}^n{a_ib_i} \quad} \]
Soit deux vecteurs \(\vec{a}\) et \(\vec{b}\) dont on connait les composantes dans une base orthonormée :
\[ \vec{a} = \begin{pmatrix}a_1\\a_2\end{pmatrix} \quad ,\quad \vec{b} = \begin{pmatrix} b_1\\b_2\end{pmatrix} \]
On sait que le produit scalaire entre \(\vec{a}\) et \(\vec{b}\) est défini par :
\[ \vec{a} \cdot \vec{b} = \|\vec{a} \| \cdot \|\vec{b}\| \cdot \cos\theta \]
Où \(\theta\) est l’angle entre \(\vec{a}\) et \(\vec{b}\).
Si on cherche à déterminer l’angle \(\theta\), on peut l’écrire sous la forme :
\[ \cos\theta = \frac{\vec{a} \cdot \vec{b}}{\|\vec{a} \| \cdot \|\vec{b}\|} \]
Mais puisqu’on connait les composantes de \(\vec{a}\) et \(\vec{b}\) dans une base orthonormée, on peut calculer \(\vec{a} \cdot \vec{b}\) en composantes :
\[ \vec{a} \cdot \vec{b} = \begin{pmatrix} a_1\\a_2\end{pmatrix} \cdot \begin{pmatrix}b_1\\b_2\end{pmatrix} = a_1 b_1 + a_2 b_2 \]
On peut également calculer les normes de \(\vec{a}\) et \(\vec{b}\) en composantes :
\[ \|\vec{a} \| = \sqrt{a_1^2 + a_2^2} \quad ,\quad \|\vec{b} \| = \sqrt{b_1^2 + b_2^2} \]
On a alors finalement que :
\[ \boxed{ \quad \theta = \arccos \left( \frac{a_1 b_1 + a_2 b_2}{\sqrt{a_1^2 + a_2^2} \cdot \sqrt{b_1^2 + b_2^2}} \right) \quad} \]
On se pose le problème suivant :
Soit \(\vec{a}\) un vecteur de \(\pi\) dont les composantes sont connues dans la base canonique : \(\vec{a} = \begin{pmatrix}a_x\\a_y\end{pmatrix}\) .
On cherche les composantes de tous les vecteurs perpendiculaires à \(\vec{a}\).
On voit que la solution au problème n’est pas unique ! On va alors réduire les possibilités en exigeant que \(\|\vec{b}\| = \|\vec{a} \| = \sqrt{a_x^2 + a_y^2}\)
On pose alors \(\vec{b} = \begin{pmatrix}x\\y\end{pmatrix}\).
On sait alors :
\[ \begin{align*} & \vec{b} \perp \vec{a} \\\\ \vec{a} \cdot \vec{b} &= \|\vec{a} \| \cdot \|\vec{b} \| \cdot \cos\theta \\\\ &= \|\vec{a} \| \cdot \|\vec{b} \| \cdot \underbrace{\cos90}_{= 0} \\\\ \Rightarrow \quad & \boxed{ \quad \vec{a} \cdot \vec{b} = 0 \quad} \end{align*} \]
On a donc :
\[ \left\{ \begin{array}{lr} a_x x + a_y y = 0 & \quad\text{(perpendiculaires)}\\ x^2 + y^2 = a_x^2 + a_y^2 & \quad\text{(m\^eme norme)} \end{array} \right. \]
C’est donc un système de deux équations à deux inconnues \(x\) et \(y\) :
\[ \begin{align*} x&= \frac{-a_y}{a_x} \cdot y \\\\ \Rightarrow \quad a_x^2 + a_y^2 &= \left( \frac{-a_y}{a_x} \cdot y \right) ^2 + y^2 \\\\ &= \left( \frac{a_y^2}{a_x^2} + 1 \right) \cdot y^2 \\\\\\ \Rightarrow \quad y^2 &= \frac{a_x^2 + a_y^2}{\frac{a_y^2}{a_x^2} + 1} = \frac{(a_x^2 + a_y^2) \cdot a_x^2}{a_y^2 + a_x^2} = a_x^2 \end{align*} \]
Ce qui donne finalement :
\[ \begin{array}{lcl} y_1 = a_x & \Rightarrow & x_1 = -a_y \\ y_2 = -a_x & \Rightarrow & x_2 = a_y \end{array} \]
On a donc deux solutions :
\[ \left\{ \begin{array}{ll} \vec{b} _1 = \begin{pmatrix}-a_y\\a_x\end{pmatrix}\\\\ \vec{b} _2 = \begin{pmatrix}a_y\\-a_x\end{pmatrix} = -\vec{b} _1 \end{array} \right. \]
Si on renonce à exiger que \(\|\vec{b} \| = \| \vec{a} \|\), on a le résultat général suivant :
Dans un repère orthonormé :
\[ \boxed{ \quad \vec{a} = \begin{pmatrix}a_x\\a_y\end{pmatrix} \perp \vec{b} = \lambda\begin{pmatrix}-a_y\\a_x\end{pmatrix} \quad ,\forall \lambda\in \mathbb{R}^* \quad} \]
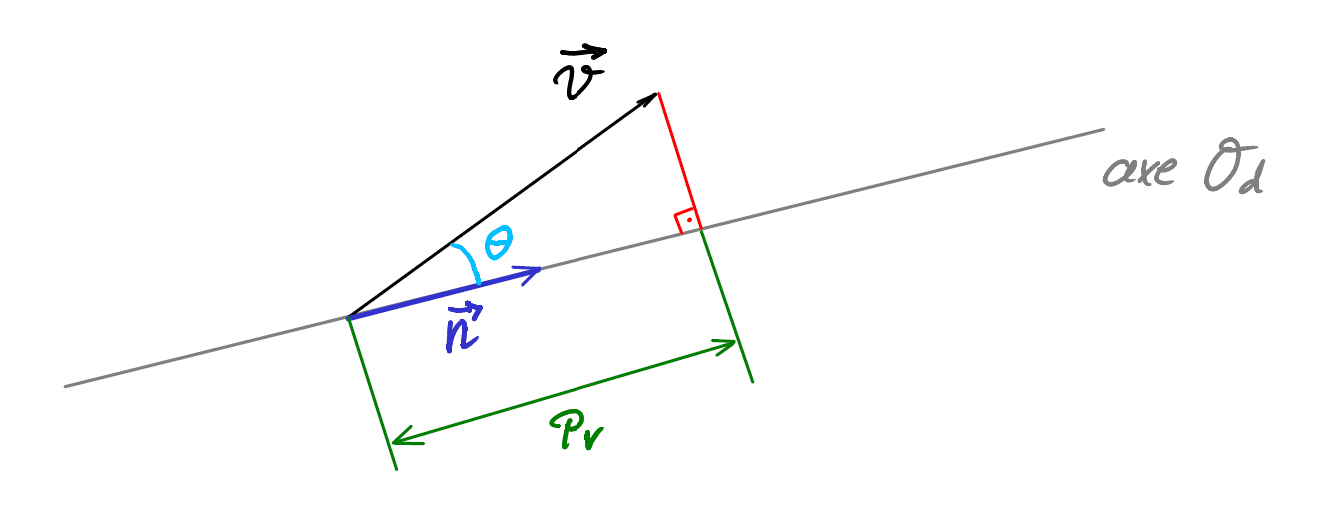
\(P_V\) est un scalaire : c’est la longueur de la projection orthogonale de \(\vec{v}\) sur l’axe \(\mathcal{O}_d\).
Soit \(\vec{n}\) un vecteur unitaire (de norme 1) colinéaire à l’axe \(\mathcal{O}_d\). On a alors :
\[ \vec{v} \cdot \vec{n} = \|\vec{v} \| \cdot \underbrace{\|\vec{n} \|}_{=1} \cdot \cos\theta = \underbrace{\|\vec{v} \| \cdot \cos\theta}_{P_V} \\\\ \Rightarrow \quad \boxed{ \quad \vec{v} \cdot \vec{n} = P_V \quad} \]
On peut donc énoncer le résultat suivant :
La projection orthogonale \(P_V\) de \(\vec{v}\) sur l’axe \(\mathcal{O}_d\) est donnée par le produit scalaire \(\vec{v} \cdot \vec{n}\), où \(\vec{n}\) est un vecteur unitaire dans la direction de \(\mathcal{O}_d\).
La droite \(d\) est un sous-ensemble des points du plan \(\pi\). On cherche le meilleur moyen de “générer” ce sous-ensemble.
Pour cela, on suit la procédure suivante :
On prend un point quelconque \(A\) appartenant à la droite \(d\). On lui ajoute un certain nombre de fois (\(\lambda\)) le vecteur \(\vec{v}\), un vecteur ayant la même direction que la droite \(d\). En variant continuellement \(\lambda\), on peut alors atteindre l’ensemble de tous les points \(P\) appartenant à la droite \(d\).
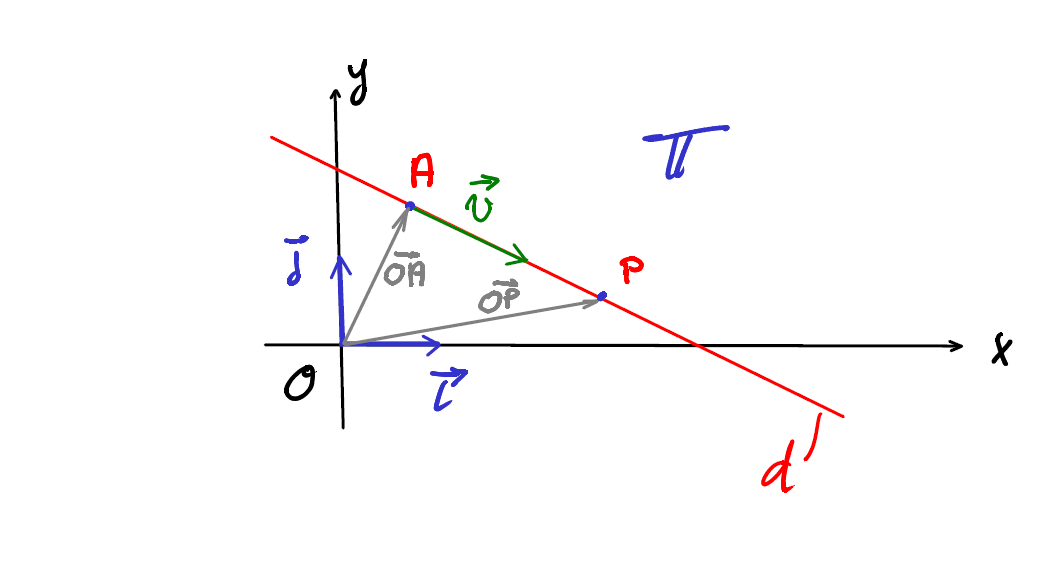
\[ \boxed{ \quad \overrightarrow{OP}= \overrightarrow{OA}+ \lambda \vec{v} \quad}\quad \Rightarrow \quad \boxed{ \quad P \in d \quad} \]
On peut alors définir une droite \(d \in \pi\) comme étant l’ensemble des points suivants :
\[ \boxed{ \quad d = \left\{ P(x,y) \mid \overrightarrow{OP} = \overrightarrow{OA} + \lambda \vec{v} \right\} \quad} \]
Avec :
Soit un point \(P(x,y) = \begin{pmatrix}x\\y\end{pmatrix}\) appartenant à la droite \(d\).
Tout point \(P\) appartenant à la droite \(d\) s’écrit alors :
\[ \boxed{ \quad \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}a_1\\a_2\end{pmatrix} + \lambda \begin{pmatrix}v_1\\v_2\end{pmatrix} \quad} \]
\[ \boxed{ \quad \overrightarrow{OP}= \overrightarrow{OA}+ \lambda \vec{v} \quad} \]
Avec \(A(a_1,a_2) \in d\) et \(\vec{v} = \begin{pmatrix}v_1\\v_2\end{pmatrix}\) parallèle à \(d\).
On peut alors définir les équations paramétriques de \(d\) comme étant deux équations scalaires équivalentes à une équation vectorielle :
\[ \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}a_1\\a_2\end{pmatrix} + \lambda \begin{pmatrix}v_1\\v_2\end{pmatrix} \quad \Rightarrow \quad \boxed{ \quad \left\{ \begin{array}{l} x = a_1 + \lambda v_1 \\ y = a_2 + \lambda v_2 \end{array} \right. \quad} \]
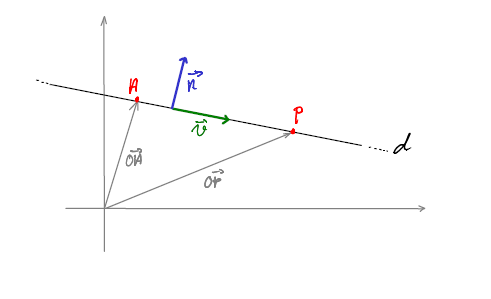
Soient les vecteurs suivants :
\[ \begin{array}\\ \overrightarrow{OA} = \begin{pmatrix}a_1\\a_2\end{pmatrix} \in d & & \overrightarrow{OP} = \begin{pmatrix}x\\y\end{pmatrix} \in d\\\\ \vec{v} = \begin{pmatrix}v_1\\v_2\end{pmatrix} \parallel d & & \vec{n} = \begin{pmatrix}n_1\\n_2\end{pmatrix} \perp d \end{array} \]
Par la règle de Chasles, on a
\[ \overrightarrow{AP} = \overrightarrow{OP}-\overrightarrow{OA} = \begin{pmatrix}x-a_1\\y-a_2\end{pmatrix} \]
Et puisque \(\overrightarrow{AP}\perp \vec{n}\) :
\[ \boxed{ \quad \overrightarrow{AP} \cdot \vec{n} =0 \quad} \]
Dans une base orthonormée, ce produit scalaire se calcule simplement :
\[ \begin{pmatrix}x-a_1\\y-a_2\end{pmatrix} \cdot \begin{pmatrix}n_1\\n_2\end{pmatrix} = (x-a_1) \cdot n_1 + (y-a_2) \cdot n_2 = 0 \]
\[ \Leftrightarrow \quad n_1 x + n_2 y = n_1 a_1 + n_2 a_2 = c \]
Ainsi, l’équation d’une droite \(d\) perpendiculaire au vecteur \(\vec{n} = \begin{pmatrix}n_1\\n_2\end{pmatrix}\) est donnée par :
\[ \boxed{ \quad d : n_1 x + n_2 y = c \quad} \]
On connait \(d : n_1 x + n_2 y = c\).
On peut alors donner le vecteur \(\vec{v} = \begin{pmatrix}-n_2\\n_1\end{pmatrix} \parallel d\) ce qui nous suffit pour donner la forme paramétrique de \(d\) :
\[ d : \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}a_1\\a_2\end{pmatrix} + \lambda \begin{pmatrix}-n_2\\n_1\end{pmatrix} \]
Où \(A(a_1,a_2)\) est point quelconque de \(d\). Il existe ainsi une infinité de possibilité. On peut alors simplement poser \(a_1 = 0\) et trouver ensuite la valeur de \(a_2\) :
\[ \begin{align*} & n_1 \cdot 0 + n_2 \cdot a_2 = c \\\\ \quad \Rightarrow \quad & a_2 = \frac{c}{n_2} \end{align*} \]
Donc \(A(0,\frac{c}{n_2} ) \in d\).
Les équations paramétriques d’une droite dont l’équation cartésienne est \(d : n_1 x + n_2 y = c\) sont données par :
\[ \boxed{ \quad d : \begin{pmatrix}x\\y\end{pmatrix} = \begin{pmatrix}0\\\frac{c}{n_2} \end{pmatrix} + \lambda \begin{pmatrix}-n_2\\n_1\end{pmatrix} \quad} \]
En partant des équations :
\[ \left\{ \begin{array}{l} x = a_1 + \lambda v_1 \\ y = a_2 + \lambda v_2 \end{array} \right. \]
On cherche une relation directe entre \(x\) et \(y\) sans le paramètre \(\lambda\). Il suffit alors d’éliminer \(\lambda\).
\[ \begin{align*} & \left\{ \begin{array}{l} x = a_1 + \lambda v_1 \\ y = a_2 + \lambda v_2 \end{array} \right. \\\\ \Leftrightarrow \quad& \left\{ \begin{array}{l} v_2 x = v_2 a_1 + \lambda v_1 v_2 \\ v_1 y = v_1 a_2 + \lambda v_1 v_2 \end{array} \right. \\\\ \Leftrightarrow \quad & v_2 x -v_1 y = v_2 a_1 - v_1a_2 \end{align*} \]
Ainsi, l’équation cartésienne d’une droite dont les équations paramétriques sont
\[ \left\{ \begin{array}{l} x = a_1 + \lambda v_1 \\ y = a_2 + \lambda v_2 \end{array} \right. \]
est donnée par :
\[ \boxed{ \quad v_2 x -v_1 y = v_2 a_1 - v_1a_2 \quad} \]
Par définition, la distance \(\delta\) entre un point \(P\) et une droite \(d\) est la longueur du chemin le plus court reliant \(P\) et \(d\). Ce chemin est un segment rectiligne perpendiculaire à \(d\).
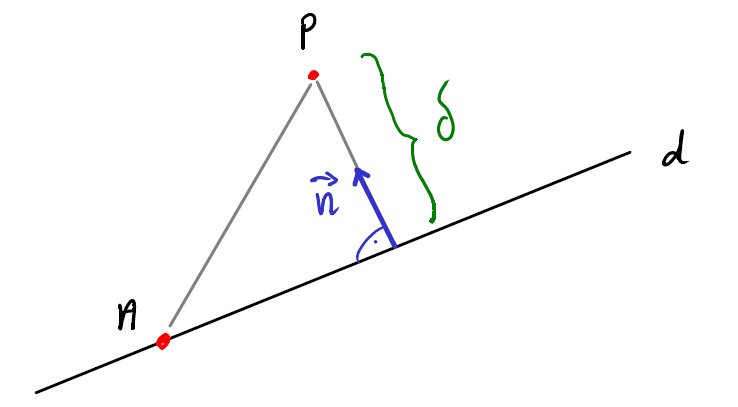
On remarque que \(\delta\) est la projection orthogonale de \(\overrightarrow{AP}\) dans la direction de \(\vec{n}\).
D’après §3.2.4, on peut poser :
\[ \boxed{ \quad \delta = \vert{\overrightarrow{AP}\cdot \frac{\vec{n} }{\| \vec{n} \|}}\vert \quad} \]
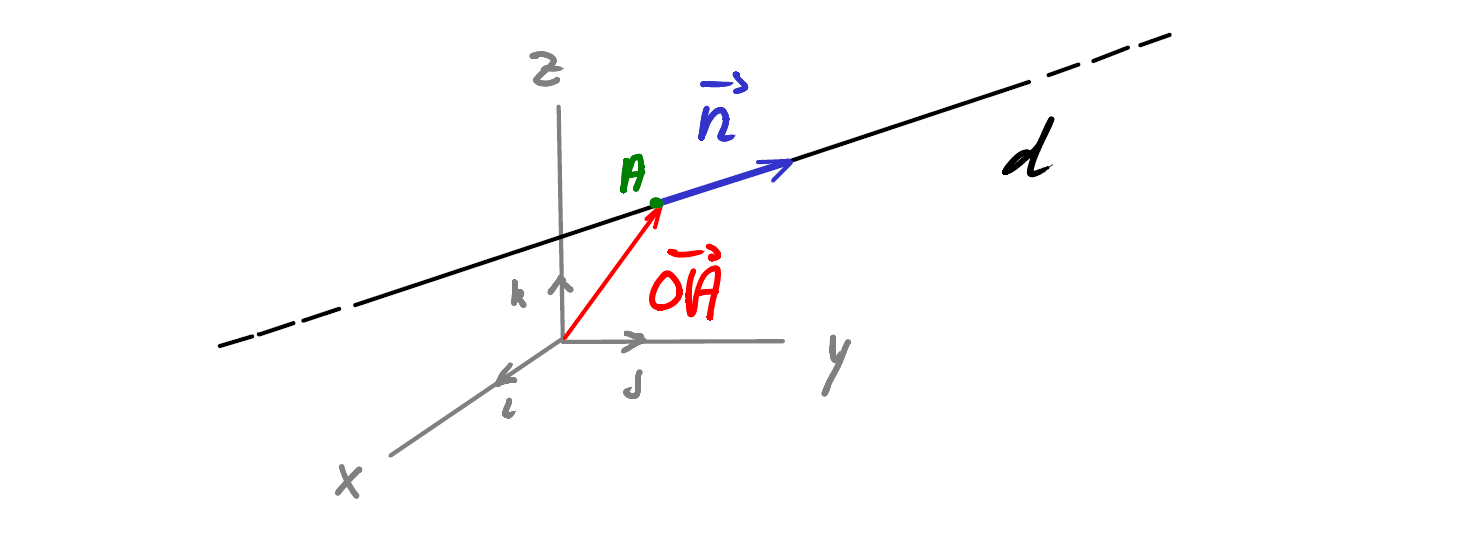
Soient \(A(a_1,a_2,a_3)\) et \(\vec{n} =\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}\), alors tout point \(P(x,y,z) \in d\) s’écrira comme étant :
\[ \boxed{ \quad \overrightarrow{OP} = \overrightarrow{OA} + \lambda \cdot \vec{n} \quad} \quad , \lambda \in \mathbb{R} \]
En écrivant cette équation en composantes, on obtient les 3 équations paramétriques d’une droite de l’espace :
\[ \begin{align*} & \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} + \lambda \begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix} \\\\ \Rightarrow \quad & \boxed{ \quad \left\{ \begin{array}{} x = a_1 + \lambda n_1\\ y = a_2 + \lambda n_2\\ z = a_3 + \lambda n_2 \end{array} \right. \quad} \end{align*} \]
Attention : il n’existe pas une équation cartésienne d’une droite de l’espace.
Le produit vectoriel de \(\vec{a}\) et \(\vec{b}\), deux vecteurs de l’espace, noté \(\vec{a} \times \vec{b}\) , est un nouveau vecteur tel que :

La norme \(\| \vec{a}\times\vec{b}\|\) est égale à la surface \(S\) du parallélogramme engendré par \(\vec{a}\) et \(\vec{b}\).
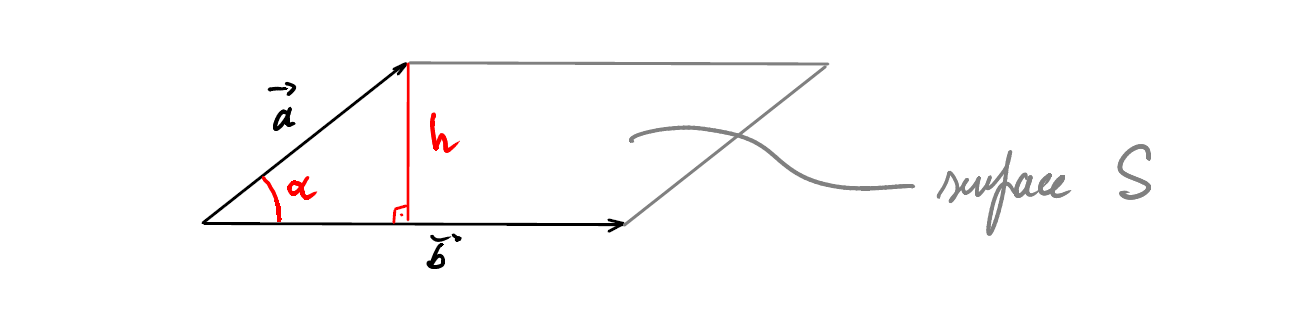
Preuve :
\[ \begin{align*} \left . \begin{array}{l} h = \| \vec{a} \| \cdot \sin\alpha \\ S= \|\vec{b} \| \cdot h \end{array} \right\} \quad \Rightarrow \quad S&= \|\vec{a} \| \cdot \|\vec{b} \| \cdot \sin\alpha =\| \vec{a}\times\vec{b}\| \end{align*} \]
Soient \(\pi\) un plan tel que \(\pi \perp \vec{a}\) et \(\vec{b} _{\perp}\) , la projection de \(\vec{b}\) sur \(\pi\).
Alors \(\boxed{ \quad \vec{a}\times\vec{b} = \vec{a}\times\vec{b}_{\perp}\quad}\)
\[ \boxed{ \quad \begin{align*} A. \quad & \vec{a}\times\vec{\lambda b} = \lambda \vec{a}\times\vec{b} = \lambda \left( \vec{a}\times\vec{b} \right) \\\\ B. \quad & \vec{a}\times \left(\vec{b} + \vec{c} \right) = \vec{a}\times\vec{b}+ \vec{a}\times\vec{c} \end{align*} \quad} \]
Soit \(\mathcal{R} = \left(\mathcal{O} , \left\{ \vec{i} , \vec{j} , \vec{k} \right\}\right)\) un repère de l’espace \(\mathcal{E}\). Soient également \(\vec{a}\) et \(\vec{b}\) deux vecteurs quelconques dans \(\mathcal{E}\). On a que :
\[ \left. \begin{array}{l} \vec{a} = a_1 \cdot \vec{i} + a_2 \cdot \vec{j} + a_3 \cdot \vec{k} \\ \vec{b} = b_1 \cdot \vec{i} + b_2 \cdot \vec{j} + b_3 \cdot \vec{k} \end{array} \right\} \Rightarrow \quad \vec{a} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} \space , \quad \vec{b} = \begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix} \]
Grâce à la propriété 3, on peut calculer produit vectoriel \(\vec{a} \times \vec{b}\) :
\[ \begin{align*} \vec{a}\times\vec{b} &= \left( a_1 \vec{i} + a_2 \vec{j} + a_3 \vec{k} \right) \times \left(b_1 \vec{i}+ b_2 \vec{j} +b_3 \vec{k} \right) \\\\ &= a_1b_1 \left(\vec{i} \times \vec{i} \right) + a_1b_2 \left(\vec{i}\times\vec{j}\right) + a_1b_3 \left(\vec{i}\times\vec{k}\right) \\\\ &+ a_2b_1 \left(\vec{j}\times\vec{i}\right) + a_2b_2 \left(\vec{j}\times\vec{j}\right) + a_2b_3 \left(\vec{j}\times\vec{k}\right) \\\\ &+ a_3b_1 \left(\vec{k}\times\vec{i}\right) + a_3 b_2 \left(\vec{k}\times\vec{j}\right) + a_3b_3 \left(\vec{k}\times\vec{k}\right) \end{align*} \]
On voit que l’on peut calculer \(\vec{a}\times\vec{b}\) à partir des composantes de $ $ et $ $ seulement si on connait les le produit vectoriel des vecteurs de base entre eux.
Si on se trouve dans un repère orthonormé \(\mathcal{R} = \left(\mathcal{O} , \left\{ \vec{i} , \vec{j} , \vec{k} \right\}\right)\) on peut alors calculer le produit vectoriel \(\vec{a}\times\vec{b}\) de cette manière :
\[ \begin{align*} \vec{a}\times\vec{b} &= \left( a_1 \vec{i} + a_2 \vec{j} + a_3 \vec{k} \right) \times \left(b_1 \vec{i}+ b_2 \vec{j} +b_3 \vec{k} \right) \\\\ &= a_1b_1 \underbrace{\left(\vec{i} \times \vec{i} \right)}_{\vec{0}} + a_1b_2 \underbrace{\left(\vec{i}\times\vec{j}\right)}_{\vec{k}} + a_1b_3 \underbrace{\left(\vec{i}\times\vec{k}\right)}_{-\vec{j} } \\\\ &+ a_2b_1 \underbrace{\left(\vec{j}\times\vec{i}\right)}_{- \vec{k}} + a_2b_2 \underbrace{\left(\vec{j}\times\vec{j}\right)}_{\vec{0}} + a_2b_3 \underbrace{\left(\vec{j}\times\vec{k}\right)}_{\vec{i}} \\\\ &+ a_3b_1 \underbrace{\left(\vec{k}\times\vec{i}\right)}_{\vec{j}} + a_3 b_2 \underbrace{\left(\vec{k}\times\vec{j}\right)}_{- \vec{i}} + a_3b_3 \underbrace{\left(\vec{k}\times\vec{k}\right)}_{\vec{0}} \\\\ &= \left( a_2b_3 -a_3b_2 \right) \cdot \vec{i} + \left(a_3b_1 - a_1b_3\right) \cdot \vec{j} + \left(a_1b_2 - a_2b_1\right) \cdot \vec{k} \end{align*} \]
On a donc le résultat fondamental suivant :
Si on connait les composantes des vecteurs \(\vec{a}\) et \(\vec{b}\) dans un repère orthonormé, les composantes du produit vectoriel \(\vec{a}\times\vec{b}\) sont données par :
\[ \boxed{ \quad \vec{a} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} \space , \space \vec{b} = \begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix} \Rightarrow \quad \vec{a}\times\vec{b} = \begin{pmatrix}a_2b_3 - a_3b_2\\a_3b_1 - a_1b_3\\a_1b_2-a_2b_1\end{pmatrix} \quad} \]
\[ \boxed{ \quad \begin{array}{ll} 1. & \vec{a}\times\vec{b} = - \vec{b}\times\vec{a} \\\\ 2. & \left(\lambda \vec{a} \right) \times \vec{b} = \lambda \cdot \left(\vec{a}\times\vec{b}\right) \\\\^ 3. & \vec{a} \times \left(\vec{b} + \vec{c} \right) = \vec{a}\times\vec{b} + \vec{a}\times\vec{c} \\\\ 4. & \vec{a}\times\vec{b} \neq \vec{0} \quad \Leftrightarrow \quad \vec{a} \text { et } \vec{b} \space \text{ indépendants}\\\\ 5. & \vec{a} \times \vec{a} = \vec{0} \\\\ 6. & \vec{a} \cdot \left(\vec{a}\times\vec{b}\right) = \vec{b} \cdot \left(\vec{a}\times\vec{b}\right) = 0\\\\ 7. & \vec{a} \times (\vec{b} \times \vec{c} ) = \left(\vec{a} \cdot \vec{c} \right) \cdot \vec{b} - \left(\vec{a} \cdot \vec{c} \right) \cdot \vec{c} \\\\ 8. &\| \vec{a}\times\vec{b}\| ^2 + \left(\vec{a} \cdot \vec{b} \right)^2 = \| \vec{a} \| ^2 \cdot \| \vec{b} \|^2 \end{array} \quad} \]
Attention : le produit vectoriel n’est pas associatif !
Soit un repère de l’espace \(\left(\mathcal{O}, \left\{ \vec{i} , \vec{j} , \vec{k} \right\}\right)\) et un plan \(\pi\) dans cet espace. Soient encore un point \(A(a_1,a_2,a_3)\) appartenant à \(\pi\) et deux vecteurs indépendant \(\vec{u}\) et \(\vec{v}\) dans le plan \(\pi\).
Tout point \(P(x,y,z) \in \pi\) est alors une combinaison linéaire des vecteurs \(\vec{u}\) et \(\vec{v}\).
On peut ainsi traduire cet énoncé par l’équation vectorielle suivante :
\[ \pi : \quad \boxed{ \quad \overrightarrow{OP}= \overrightarrow{OA} + \lambda \vec{u} +\mu \vec{v} \quad} \]
En notation matricielle, on a:
\[ A= (a_1,a_2,a_3) \in \pi\\\\ \vec{u} = \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}, \vec{v} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} \in \pi \quad \text { t.q. }\space \vec{u} \neq \lambda \vec{v} , \quad\forall \lambda \in \mathbb{R} \]
L’équation paramétrique du plan \(\pi\) est donc donnée par :
\[ \pi : \quad \boxed{ \quad \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} + \lambda \cdot \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix} + \mu \cdot \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} \quad} \]
Cette équation est alors vraie, peu importe le repère utilisé.
Soient \(\vec{n}\) un vecteur perpendiculaire au plan \(\pi\) et \(A\) un point appartenant au plan.
Comme \(\vec{n} \perp \overrightarrow{AP}\), on a \(\vec{n} \cdot \overrightarrow{AP}=0\).
On a alors :
\[ A (a_1,a_2,a_3) \in \pi \quad\quad \text{ et } \quad\quad \vec{n} =\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix} \perp \pi \]
ainsi qu’un point quelconque \(P(x,y,z)\) de \(\pi\). On aura donc :
\[ \overrightarrow{AP}= \overrightarrow{OP}-\overrightarrow{OA} = \begin{pmatrix}x\\y\\z\end{pmatrix} - \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix} = \begin{pmatrix}x-a_1\\y-a_2\\z-a_3\end{pmatrix} \]
Et finalement, on a :
\[ \begin{align*} \vec{n} \cdot \overrightarrow{AP}&= n_1(x-a_1) + n_2 (a-a_2) + n_3(z-a_3)\\\\& = n_1 x + n_2 y + n_3 z - \underbrace{(n_1a_1 + n_2a_2 + n_3a_3)}_{=d} \end{align*} \]
L’équation cartésienne d’un plan \(\pi\) t.q. \(\vec{n} \perp \pi\) et \(A \in \pi\) est donnée par :
\[ \pi : \quad \boxed{ \quad n_1 x + n_2 y + n_3 z = d \quad} \]
Attention : Cette équation n’est valable que pour un repère orthonormé !
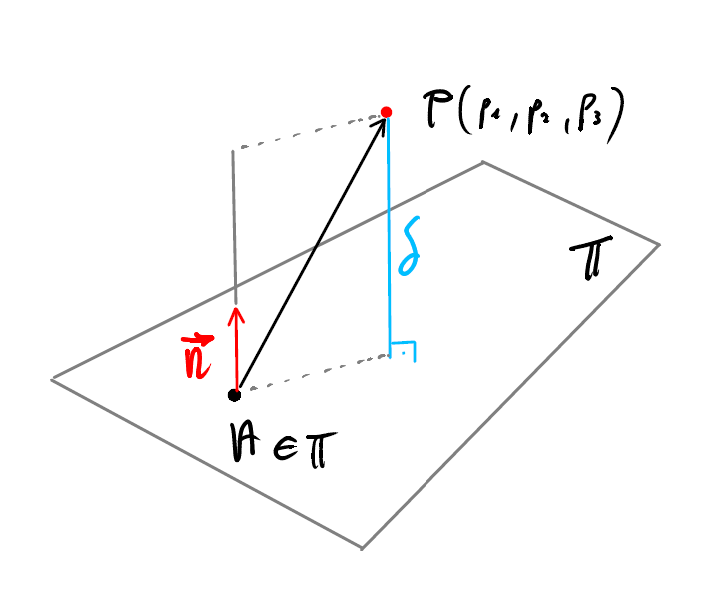
On alors :
La distance \(\delta\) entre le point \(P(p_1,p_2,p_3)\) et le plan \(\pi\) est la longueur de la projection orthogonale du vecteur \(\overrightarrow{AP}\) dans la direction du vecteur \(\vec{n}\).
On a alors :
\[ \boxed{ \quad \delta = \left\lvert\overrightarrow{AP}\cdot \frac{\vec{n} }{\| \vec{n} \|} \right\rvert \quad} \]
On a :
\[ A (a_1,a_2,a_3)\\\\ \vec{u} = \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}, \vec{v} = \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix} \]
On trouve \(\vec{n}\) et \(d\) avec :
\[ \begin{align*} &\vec{n} = \vec{u} \times \vec{v} \\\\ &d= n_1 a_1 + n_2 a_2 + n_3 a_3 \end{align*} \]
On a :
\[ \pi : n_1 x + n_2 y + n_3 z = d \]
On cherche \(A \in \pi\) et \(\vec{u} ,\vec{v} \in \pi\) On pose \(A(a_1,0,0)\), ainsi :
\[ a_1 = \frac{d}{n_1} \]
Donc : \(A(\frac{d}{n_1},0,0 )\)
On sait que \(\vec{u} \perp \vec{n}\) et \(\vec{v} \perp \vec{n}\), donc :
\[ \vec{u} \cdot \vec{n} = 0\\ \vec{v} \cdot \vec{n} = 0 \]
On peut alors simplement choisir :
\[ \vec{u} = \begin{pmatrix}-b\\a\\0\end{pmatrix}, \quad \vec{v} = \begin{pmatrix}-c\\0\\a\end{pmatrix} \]
Finalement, on a :
\[ \pi : \quad \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}\frac{d}{n_1} \\0\\0\end{pmatrix} + \lambda \begin{pmatrix}-b\\a\\0\end{pmatrix} + \mu \begin{pmatrix}-c\\0\\a\end{pmatrix} \]
Soient \(\vec{a}, \vec{b}, \vec{c}\) trois vecteurs de l’espace. On appelle produit mixte un scalaire \(m\) tel que :
\[ \boxed{ m = \vec{a} \cdot \left( \vec{b} \times \vec{c} \right) } \]
souvent noté : \(m = \left[ \vec{a}, \vec{b}, \vec{c} \right]\)
$m $ est le volume du parallélépipède construit sur les vecteurs \(\vec{a}, \vec{b}, \vec{c}\).
De plus : - Si \(m > 0\), \(\left( \vec{a}, \vec{b}, \vec{c} \right)\) est orienté positivement - Si \(m < 0\), \(\left( \vec{a}, \vec{b}, \vec{c} \right)\) est orienté négativement

Les propriétés suivantes découlent directement de la définition du produit mixte et du fait qu’il représente le volume construit sur trois vecteurs.
Le produit mixte est invariant par rotation des arguments :
\[ \boxed{ \left[ \vec{a}, \vec{b}, \vec{c} \right] = \left[ \vec{c}, \vec{a}, \vec{b} \right] = \left[ \vec{b}, \vec{c}, \vec{a} \right] } \]
Le signe du produit mixte change quand on permute deux vecteurs dans le produit vectoriel.
\[ \boxed{ \left[ \vec{a}, \vec{b}, \vec{c} \right] = - \left[ \vec{a}, \vec{c}, \vec{b} \right] \\\\ \left[ \vec{b}, \vec{c}, \vec{a} \right] = - \left[ \vec{b}, \vec{a}, \vec{c} \right] \\\\ \left[ \vec{c}, \vec{a}, \vec{b} \right] = - \left[ \vec{c}, \vec{b}, \vec{a} \right] } \]
\[ \boxed{ \vec{a} \cdot \left( \vec{b} \times \vec{c} \right) = \left( \vec{a} \times \vec{b} \right) \cdot \vec{c} } \]
\[ \boxed{ \left[ \lambda \cdot \vec{a}, \vec{b}, \vec{c} \right] = \lambda \cdot \left[ \vec{a}, \vec{b}, \vec{c} \right] } \]
\[ \boxed{ \begin{align*} 1. &\quad \left[ \vec{a}_1 + \vec{a}_2, \vec{b}, \vec{c} \right] = \left[ \vec{a}_1, \vec{b}, \vec{c} \right] + \left[ \vec{a}_2, \vec{b}, \vec{c} \right] \\\\ 2. & \quad\left[ \vec{a}, \vec{b}_1 + \vec{b}_2, \vec{c} \right]= \left[ \vec{a}, \vec{b}_1, \vec{c} \right] + \left[ \vec{a}, \vec{b}_2, \vec{c} \right] \end {align*} } \]
\[ \boxed{ \left[ \vec{a}, \vec{b}, \vec{c} \right]=0 \quad \Leftrightarrow \quad \exists \lambda, \mu \in \mathbb{R} \space\text{ t.q. }\space \vec{a} = \lambda \vec{b} + \mu \vec{c} } \]
\[ \boxed{ \left[ \vec{a} + \lambda \vec{b} + \mu \vec{c}, \vec{b}, \vec{c} \right] = \left[ \vec{a}, \vec{b}, \vec{c} \right] } \]
\[ \boxed{ \left[ \vec{a}, \vec{b}, \vec{c} \right] = \det{\left( \vec{a}, \vec{b}, \vec{c} \right)} } \]
Les points \(A\), \(B\) et \(C\) définissent le plan \(\pi\)
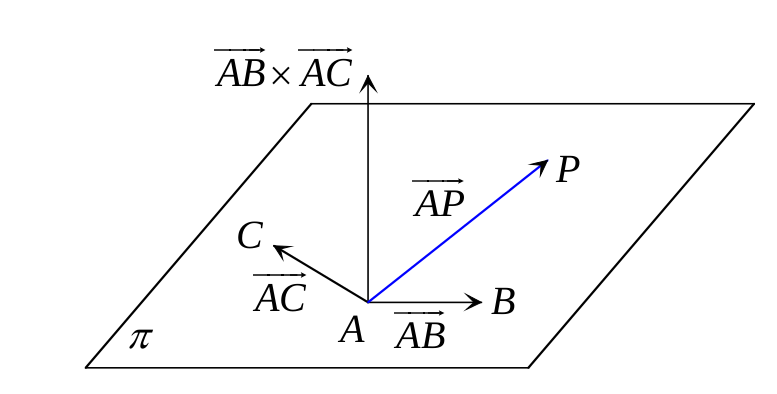
Pour tout point \(P \in \pi\) on a que :
\[ [ \overrightarrow{AP}, \overrightarrow{AB}, \overrightarrow{AC} ] = 0 \]
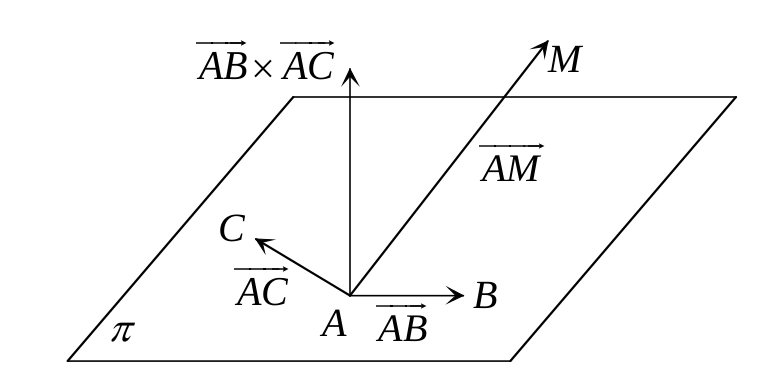
\[ \boxed{ \delta = \frac{[ \overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AM} ]}{ \| \overrightarrow{AB} \times \overrightarrow{AC} \|} } \]
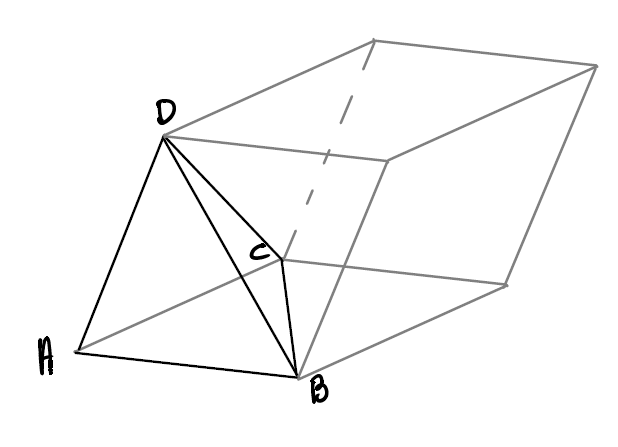
Le volume d’un tétraèdre \(ABCD\) construit sur les vecteurs \(\overrightarrow {AB}, \overrightarrow{AC}, \overrightarrow{AD}\) vaut \(\frac{1}{6}\) du volume d’un parallélépipède construit sur les même vecteur.
Un cercle \(\mathcal{C}\) est une forme particulière telle que tous les points qui la composent se trouvent à égale distance \(r\) d’un point \(C(\alpha, \beta)\), appelé centre du cercle \(\mathcal{C}\). La grandeur \(r\) est appelée rayon du cercle.
[…]
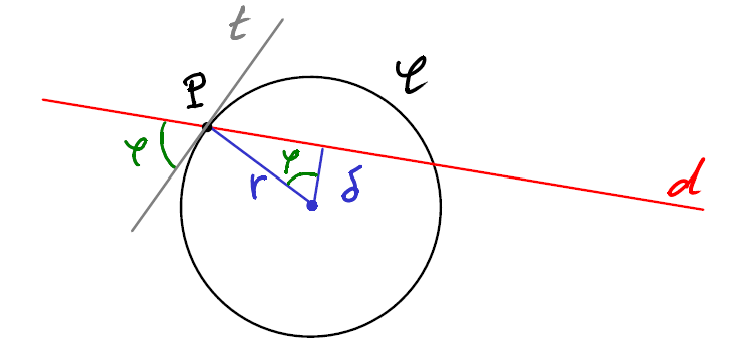
L’angle entre le cercle \(\mathcal{C}\) et la droite \(d\) au point \(P\) est défini comme l’angle entre \(d\) et \(t\), où \(t\) est la tangente au cercle au point \(P\)
D’après la figure ci-dessus, on a que \(\cos\varphi = \frac{\delta}{r}\) On trouve \(\varphi\) en calculant \(\delta\) qui est la distance entre la droite \(d\) et le centre du cercle et où \(r\) est le rayon du cercle.
On a finalement que :
\[ \delta = \frac{\vec{n}_{\perp} \cdot \overrightarrow{CQ}}{\| \vec{n}_{\perp}\|} \quad \Rightarrow \quad \varphi = \arccos{\left( \frac{\delta}{r} \right)} \]
Où \(Q\) est un point quelconque de \(d\) et \(C\) le centre du cercle \(\mathcal{C}\)
Une sphère de rayon \(r\) et de centre \(C(x_0, y_0, z_0)\) est l’ensemble des points de l’espace \(\mathcal{E}\) se trouvant à une distance \(r\) du point \(C\)
Soit alors un point \(P(x,y,z)\) quelconque appartenant à la sphère \(\sigma\). On a donc que l’équation \(\| \overrightarrow{CP} \| = r\) définit entièrement la sphère.
\[ \boxed{ \sigma : \space (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = r^2 } \]
On trouve cette équation, dite équation canonique de la sphère, en développant l’équation donnée dans la définition.
En développant les carrés et en multipliant par une constante \(a\), on obtient l’équation cartésienne générale de la sphère :
\[ \boxed{ \sigma : \space ax^2 + ay^2 + az^2 + bx + cy + dz + e = 0 } \]
Soit le point \(T\) appartenant à la sphère \(\sigma\) centrée en \(C(x_0,y_0,z_0)\). Soit également un plan \(\pi\), tangent à \(\sigma\) au point \(T(t_x,t_y,t_z)\).
On a donc que : \(\quad T \in \pi\) et \(\overrightarrow{CT} \perp \pi\)
Soit donc \(P(x,y,z)\) un point quelconque de \(\pi\), on aura alors l’équation du plan tangent à \(\pi\) :
\[ \boxed{ \overrightarrow{TP} \cdot \overrightarrow{CT} = 0 } \]