2. Nombres complexes
2. Nombres complexes2.1 Définition formelle2.1.1 Plan de Gauss2.1.2 Module et argument2.1.3 Opérations de base sur les nombres complexes1. Egalité2. Somme et différence3. Multiplication par un réel4. Multiplication par un complexe5. Conjugaison complexePropriétés du conjugué complexe 6. Quotient de deux nombres complexes2.2 Forme polaire2.2.1 Formules d'Euler et de De Moivre2.2.2 Nombres complexes sous forme polairePassage de la forme cartésienne à la forme polairePassage de la forme polaire à la forme cartésienne2.2.3 Opérations EgalitéConjugué complexeModuleArgumentProduitQuotientPuissance entière d'un nombre complexe2.2.4 Racine d'un nombre complexe2.2.5 Racines complexes dans le plan de Gauss2.3 Théorème fondamental de l'algèbre2.3.1 Rappel2.3.2 TFA2.3.3 Corollaire 1 - factorisation complète2.3.4 Corollaire 2 - racines conjuguées2.4 Fonction de la variable complexe2.4.1 Définition2.4.2 Représentation graphiqueExemple2.5 Lieux géométriques dans le plan de Gauss
2.1 Définition formelle
L'ensemble des nombres complexe est défini comme :
On note alors
2.1.1 Plan de Gauss
D'après la définition, un nombre complexe est formé d'un couple de nombre réels
On peut alors les représenter sur un plan, appelé plan de Gauss.
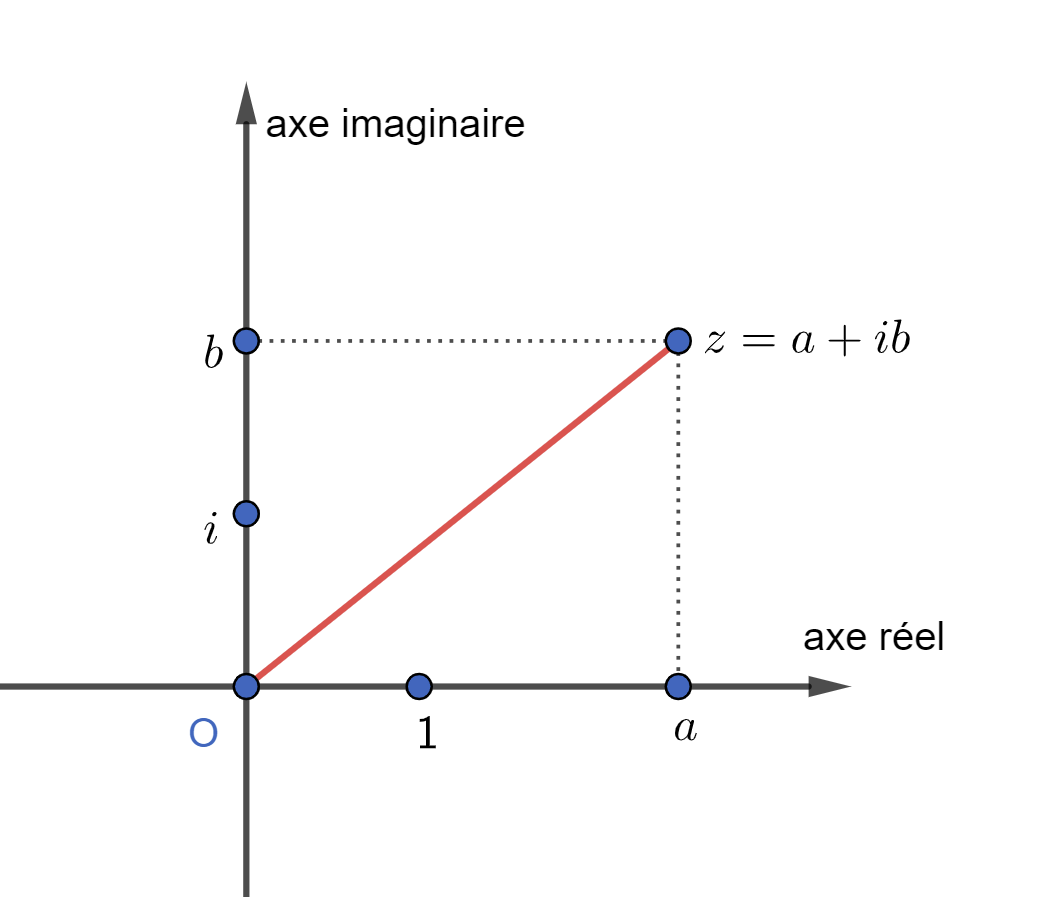
Avec cette représentation, on interprète
2.1.2 Module et argument
Avec l'introduction du plan de Gauss, on peut alors s'intéresser à la distance entre l'origine
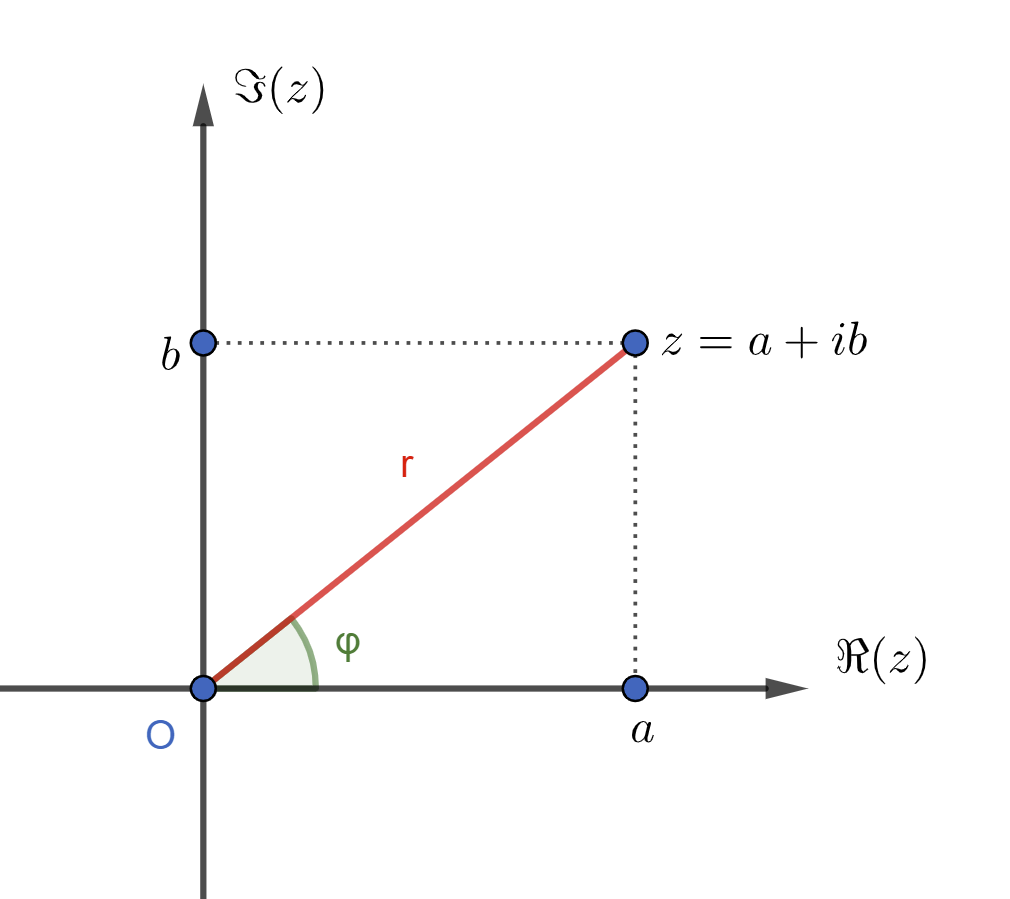
En connaissant
De la même manière, en connaissant
Dans le cas particulier où la partie réelle est nulle (
2.1.3 Opérations de base sur les nombres complexes
1. Egalité
Deux nombres complexes
2. Somme et différence
Soient
On définit la somme et différence de
On voit qu'on fait la somme ou la différence des parties réelles puis imaginaires.
Dans le plan, cela revient à faire une translation :
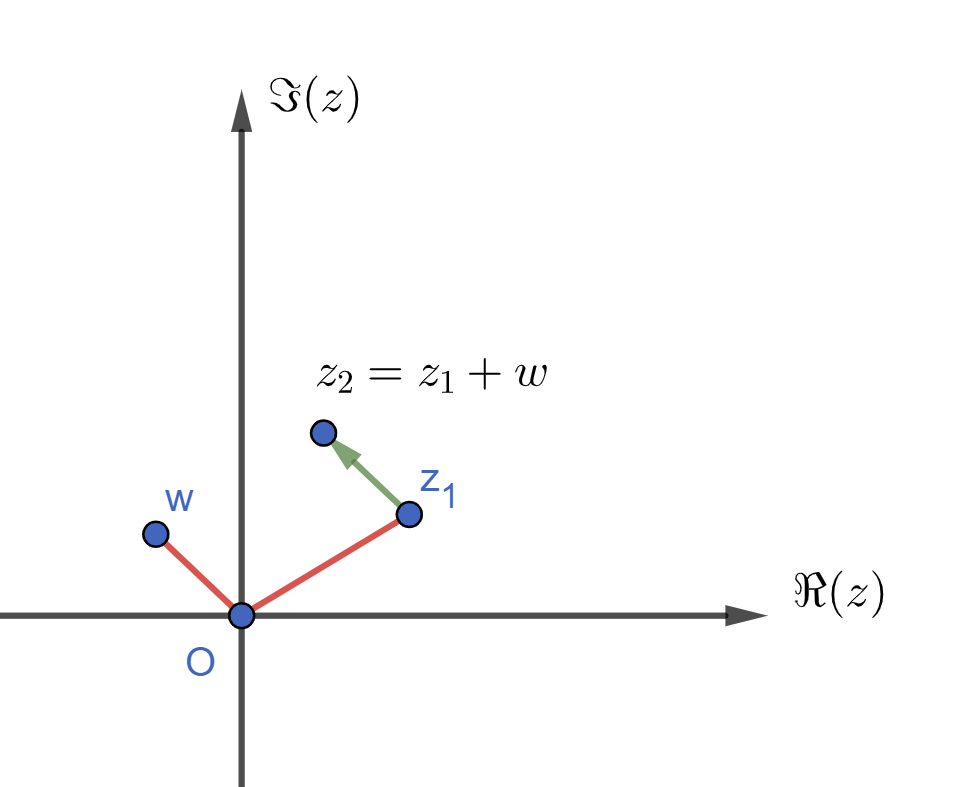
3. Multiplication par un réel
Soient
Dans le plan il s'agit d'une homothétie :
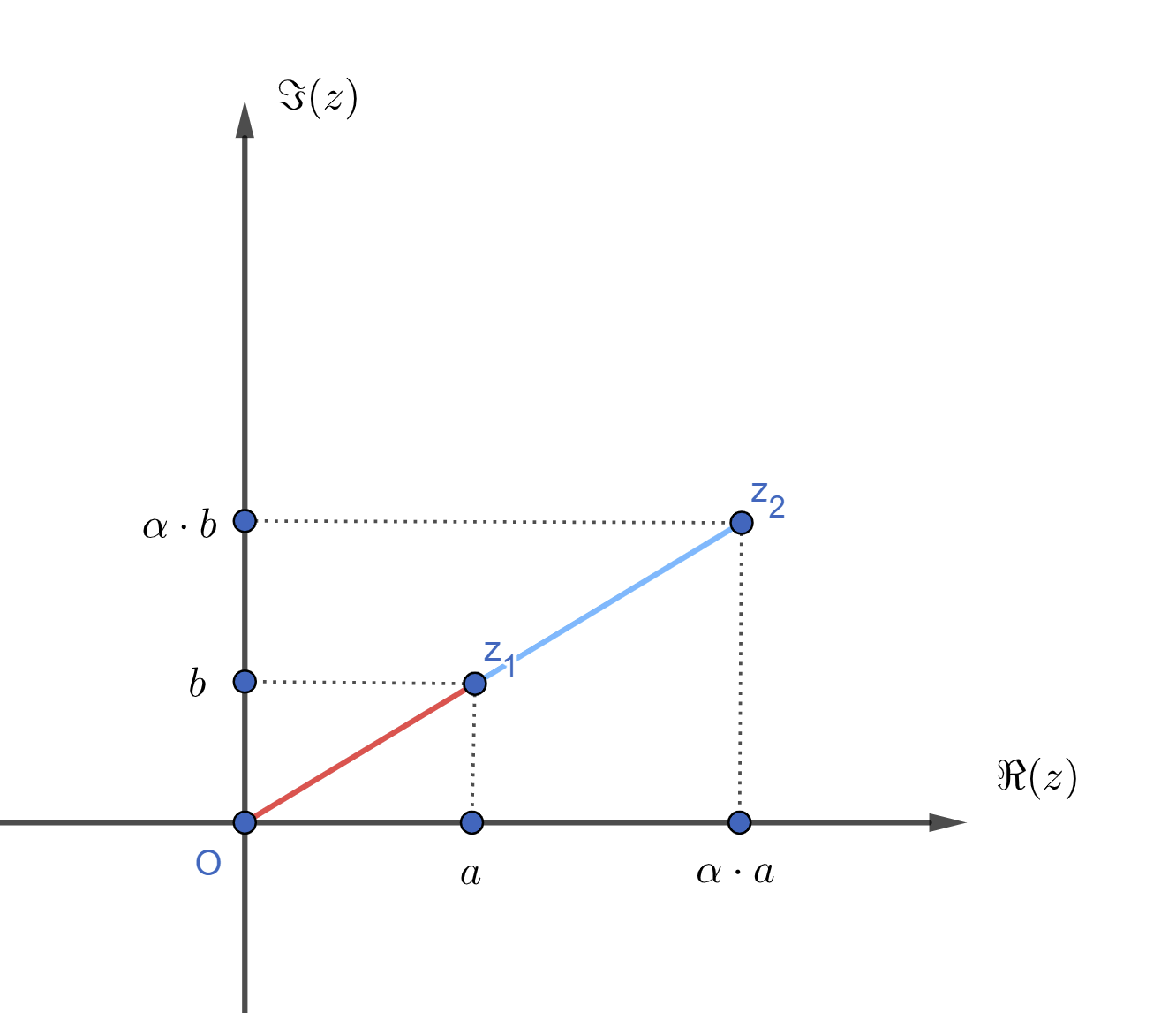
4. Multiplication par un complexe
Soient
Dans le plan de Gauss, la multiplication de deux nombres complexes consiste à :
- multiplier leur modules
- additionner leurs arguments
C'est-à-dire que :
5. Conjugaison complexe
Soient
Alors
On a alors que :
On voit que pour trouver le conjugué complexe d'un nombre, il suffit de changer le signe de sa partie imaginaire.
Dans le plan de Gauss, il s'agit d'une symétrie par rapport à l'axe des réels.
Propriétés du conjugué complexe
6. Quotient de deux nombres complexes
On sait multiplier deux nombres complexes entre eux ainsi que multiplier un complexe par un réel, on est donc capable de calculer cette expression !
Conclusion : Pour diviser deux nombres complexes, il est très avantageux de multiplier numérateur et dénominateur par le conjugué complexe du dénominateur.
Si deux nombres complexes sont donnés par leur module et leur argument, leur quotient est donné par le quotient des modules et la différences des arguments.
Autrement dit :
2.2 Forme polaire
Au lieu de représenter les nombres complexes de manière cartésienne, càd selon des coordonnées
Pour l'instant, on a
2.2.1 Formules d'Euler et de De Moivre
Selon des résultats d'analyse, on peut poser grâce aux séries de Tylor :
On va utiliser la définition de l'exponentielle pour définir l'exponentielle complexe.
On pose
Alors :
Mais on sait que
Donc :
On obtient le résultat fondamental suivant :
On appelle donc la forme polaire d'un nombre complexe
Formule de De Moivre
Grâce à la formule de Moivre, on peut poser :
Ce qui nous permet d'écrire les fonctions trigonométriques avec des exponentielles :
2.2.2 Nombres complexes sous forme polaire
image
On a donc :
avec
Passage de la forme cartésienne à la forme polaire
On a
Passage de la forme polaire à la forme cartésienne
On a
avec
2.2.3 Opérations
Egalité
Conjugué complexe
Module
Argument
Produit
Quotient
Puissance entière d'un nombre complexe
Soient
Alors :
2.2.4 Racine d'un nombre complexe
Les racines nième d'un nombre complexe
Avec
On peut écrire
Nos inconnues sont alors
On remplace dans l'équation :
Donc
On compare
On voit alors que :
2.2.5 Racines complexes dans le plan de Gauss
A COMPLETER
2.3 Théorème fondamental de l'algèbre
2.3.1 Rappel
Dans l'ensemble des nombres réels, tout polynôme peut se factoriser en produits de polynômes de 1er degré et de polynômes de 2e degré dont le delta est négatif.
2.3.2 TFA
Soit
Soit le polynôme de degré
Alors il existe exactement
.
2.3.3 Corollaire 1 - factorisation complète
Un polynôme en
Où
2.3.4 Corollaire 2 - racines conjuguées
Soient
Soit aussi le polynôme
On a alors que si
Où
2.4 Fonction de la variable complexe
2.4.1 Définition
Une fonction de la variable complexe
2.4.2 Représentation graphique
Contrairement aux fonction réelles, il n'est pas possible de dessiner le graphe d'une fonction complexe.
En effet, il faudrait une représentation en 4 dimensions !
On peut au mieux dessiner deux plans complexes : l'un représentant le domaine de départ et l'autre l'ensemble d'arrivée.
On peut par exemple représenter l'image d'une grille régulière et orthonormée par la fonction complexe
Exemple
Soit la fonction complexe
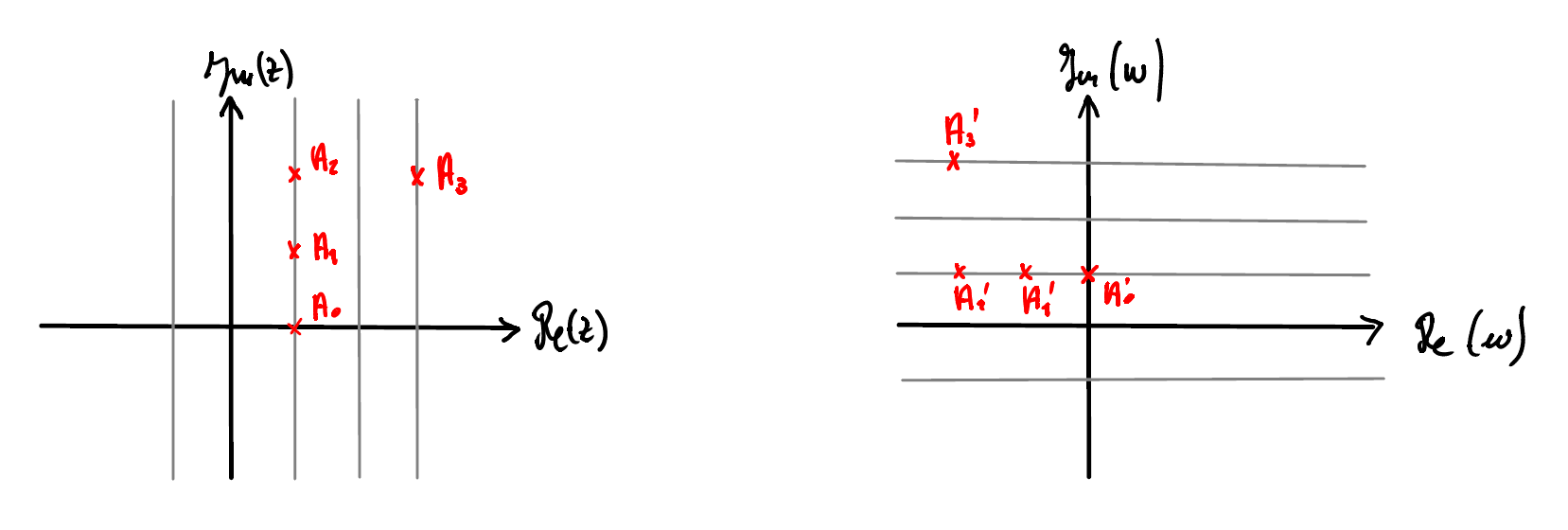
On trouve les images en ajoutant
2.5 Lieux géométriques dans le plan de Gauss
Dans le plan cartésien
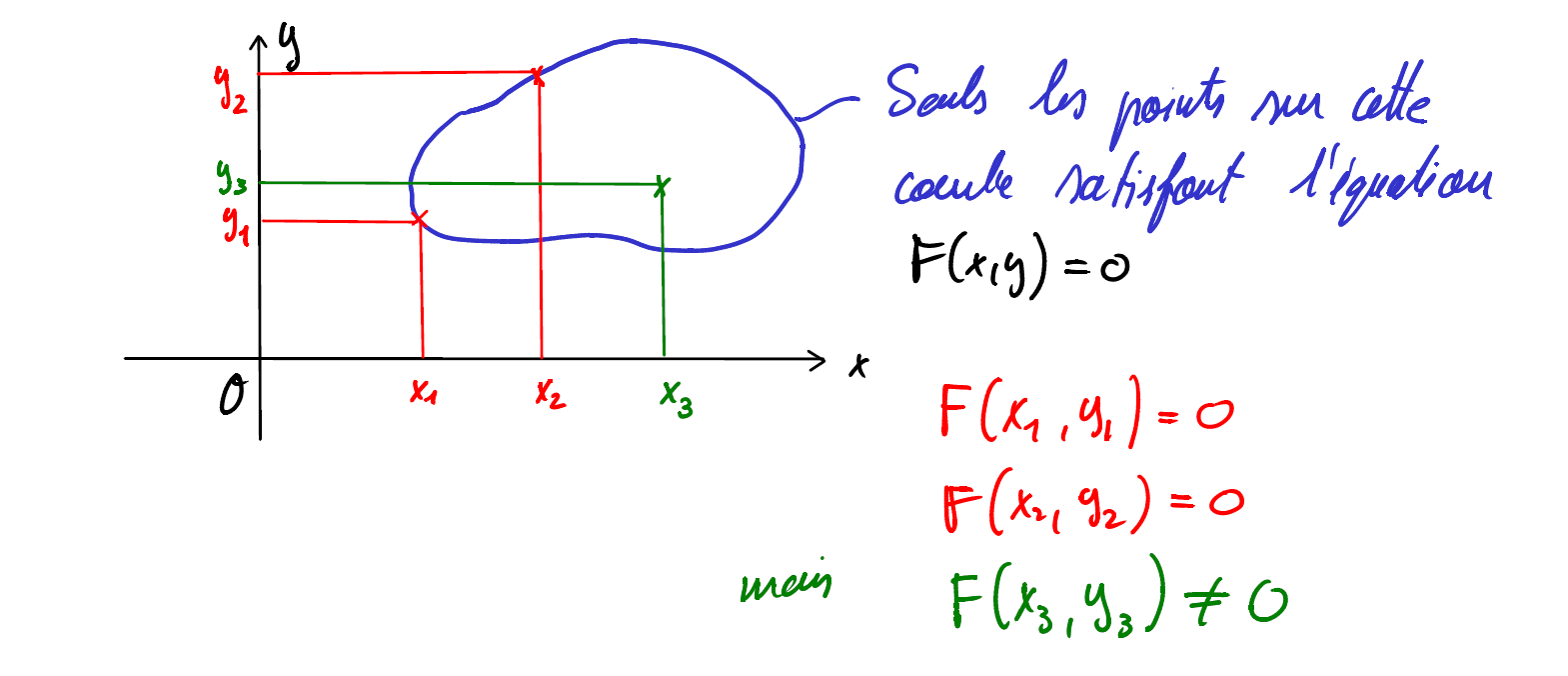
Dans le plan de Gauss, il en est de même pour les équation de la forme
Pour pouvoir dessiner la courbe définie par
On peut aussi trouver la relation entre