Chapitre 1- Trigonométrie

1.0 Introduction

• $A,B,C$$A, B, C$ sont appelés les sommets
• $a,b,c$$a,b,c$ sont les longueurs des côtés
• $\alpha ,\beta ,\gamma$$\alpha, \beta, \gamma$ sont les ouvertures des angles

1.1 Angles

Définition

Deux segments de droites issus d'un même sommet $S$$S$ forment ce qu'on appelle un angle.

1.1.1 Mesure d'un angle

On lie la mesure d'un angle à la rotation du côté initial $a$$a$ au côté final $b$$b$ :

Il faudra alors préciser deux grandeurs :

1. Dans quel sens on tourne
2. De combien on tourne

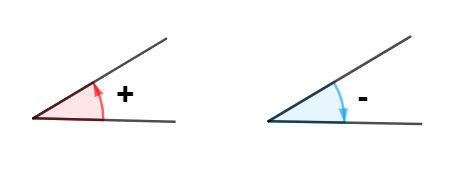
Sens d'un angle

Par convention, une rotation dans le sens :

• antihoraire est positive
• horaire est négative

Comment mesurer un angle

La mesure d'un angle consiste à préciser de combien on va tourner pour passer du côté initial au côté final.

Il y a alors deux solutions possibles :

Solution 1

On décrète que :

• Un tour complet vaut 360 unités d'angles
• Une unité d'angle est appelée degré et on la note (°)

Degrés, minutes, secondes

Au lieu d'exprimer les degrés à l'aide de nombres réels (p. ex $\theta =1.635°$$\theta=1.635°$) on subdivise chaque degré en 60 minutes et chaque minute en 60 secondes.

Solution 2

Il est possible de mesure la rotation, donc l'angle, par la longueur de l'arc de cercle décrit par le point $A$$A$ :

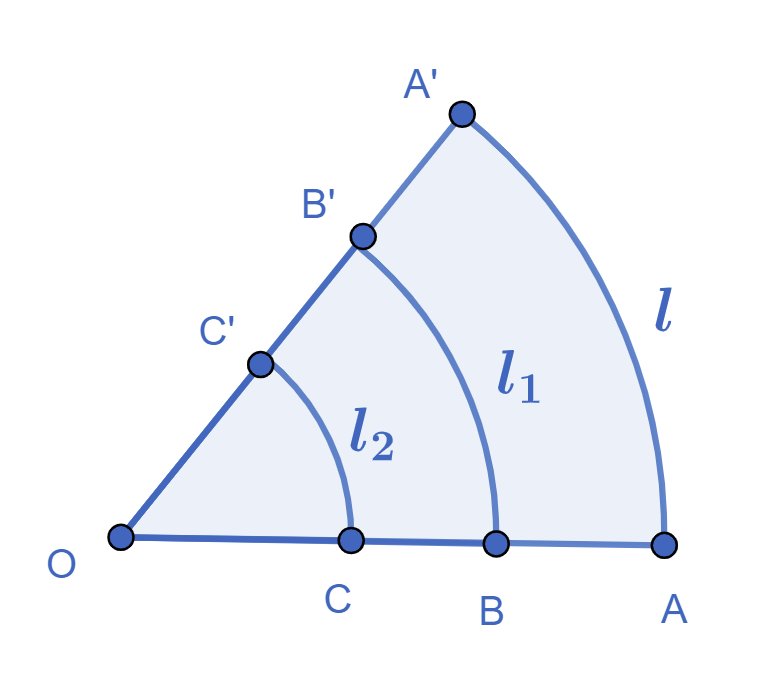
Mais telle quelle, cette solution donne des mesures différentes pour une même rotation. On remarque toutefois que les longueurs d'arc sont proportionnelles à la distance qui sépare le point de départ au sommet :

On nomme ces "unités" d'angles, des radians même si en réalité ce ne sont pas des unités mais bien un rapport de longueurs.

On peut simplement passer d'une unité à l'autre en sachant qu'un tour complet vaut $360°$$360°$ ou $2\pi$$2\pi$.

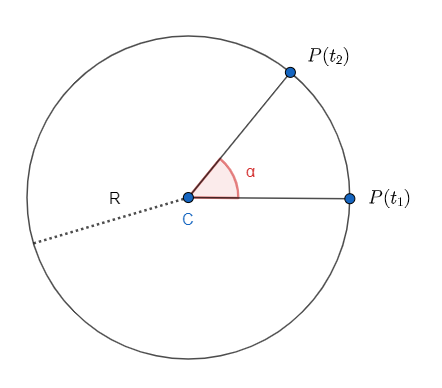
La mesure d'un angle en radians correspond à l'arc mesuré le long d'un cercle de rayon $r=1$$r=1$ appelé cercle unité ou cercle trigonométrique.

1.1.2 Vitesse angulaire

Soit un disque tournant autour de son centre $C$$C$ et observons le mouvement d'un point $P$$P$ situé à une distance $R$$R$ de $C$$C$.

On représente alors le segment $CP$$CP$ à l'instant $t_1$$t_1$ puis à l'instant $t_2$$t_2$.

Ce segment a tourné d'un angle $\alpha$$\alpha$

La vitesse du point $P$$P$ est donc proportionnelle à sa distance au centre $C$$C$.

Tous les points n'ont donc pas la même vitesse mais le rapport entre la vitesse du point et sa distance au centre est égal pour tous les points le long de la même droite.

On définit alors la vitesse angulaire $\omega$$\omega$ comme étant :

1.2 Théorèmes fondamentaux

1.2.1 Triangles homothétiques

Les triangles homothétiques, aussi appelés triangles semblables, sont des triangles de même forme mais de dimension différente.

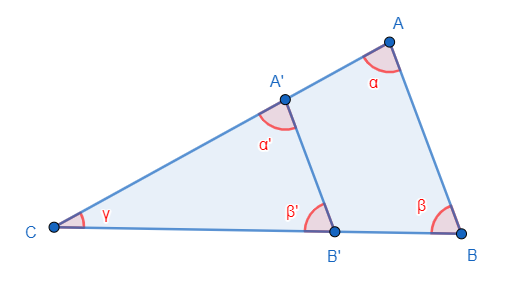
1.2.2 Théorème de Thalès

Si $A^{\prime }{B}^{\prime }$$A'B'$ est parallèle à $AB$$AB$, alors $ABC$$ABC$ et $A^{\prime }{B}^{\prime }{C}^{\prime }$$A'B'C'$ sont homothétiques.

Conséquences

1. Il existe un facteur de dilatation $\lambda$$\lambda$ reliant les dimensions de $ABC$$ABC$ et celles de $A^{\prime }{B}^{\prime }{C}^{\prime }$$A'B'C'$ avec :

   $$\lambda =\frac{CA}{C{A}^{\prime }}=\frac{CB}{C{B}^{\prime }}=\frac{AB}{A^{\prime }{B}^{\prime }}$$

2. Les angles sont conservés

1.2.3 Théorème de Pythagore

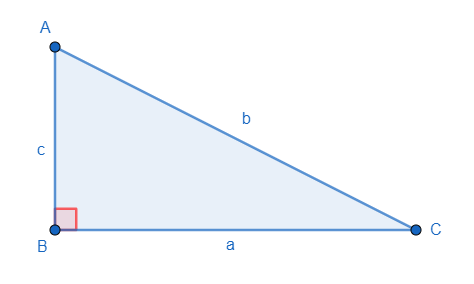
Soit un triangle $ABC$$ABC$ rectangle en $C$$C$, alors

1.3 Cercle trigonométrique

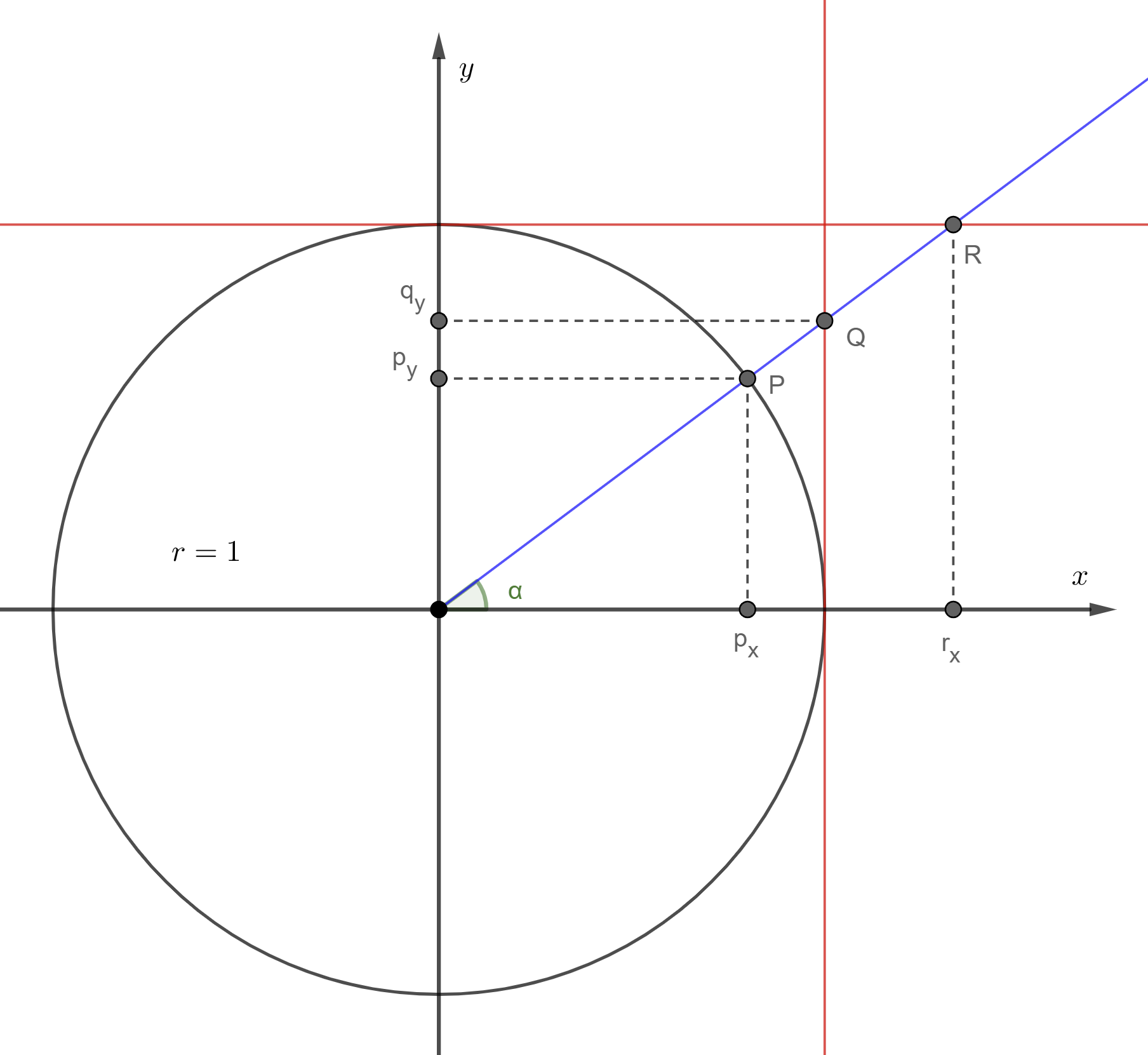
1.3.1 Définitions fondamentales

Sur le côté final de l'angle $\theta$$\theta$, on définit 3 points $P,Q$$P,Q$ et $R$$R$ ainsi que trois droites $d_1,d_2$$d_1,d_2$ et $d_3$$d_3$.

1. $P(p_x,p_y)$$P(p_x,p_y)$ est l'intersection de $d_3$$d_3$ avec $C$$C$. On définit :

   $$\begin{array}{c}{p}_x=\cos \left(\theta \right)\\ p_y=\sin \left(\theta \right)\end{array}$$

   Où on appelle $\cos \left(\theta \right)$$\cos(\theta)$ le cosinus de l'angle $\theta$$\theta$ et $\sin \left(\theta \right)$$\sin(\theta)$ le sinus de l'angle $\theta$$\theta$.

    

2. $Q(q_x,q_y)$$Q(q_x,q_y)$ est l'intersection de $d_1$$d_1$ et $d_3$$d_3$. On définit :

   $$\begin{array}{rl}& q_x=1\\ & q_y=\tan \left(\theta \right)\end{array}$$

   Où on appelle $\tan \left(\theta \right)$$\tan(\theta)$ la tangente de l'angle $\theta$$\theta$.

    

3. $R(r_x,r_y)$$R(r_x,r_y)$ est l'intersection de $d_2$$d_2$ et $d_3$$d_3$. On définit :

   $$\begin{array}{rl}& r_x=\cot \left(\theta \right)\\ & r_y=1\end{array}$$

   Où on appelle $\cot \left(\theta \right)$$\cot(\theta)$ la cotangente de l'angle $\theta$$\theta$.

    

1.3.2 Rapports trigonométriques

Grâce au théorème de Thalès, on peut trouver les coordonnées de tous les points des deux triangles rectangles semblables :

De plus, grâce aux théorèmes de Thalès et de Pythagore, on a obtenu les rapports trigonométriques suivants :

1.3.3 Angles particuliers

Pour certains angles particuliers, il est possible de donner la valeur exacte de leur sinus, cosinus et tangente.

Ces angles sont :

1.4 Fonctions trigonométriques

Jusqu'ici nous avons considérés le sinus, le cosinus et la tangente comme des définitions géométriques. A présent, nous allons les regarder comme des fonctions.

On va établir une relation de correspondance entre la valeur de l'angle et celle du sinus, du cosinus et de la tangeante.

1.4.1 Fonction sinus

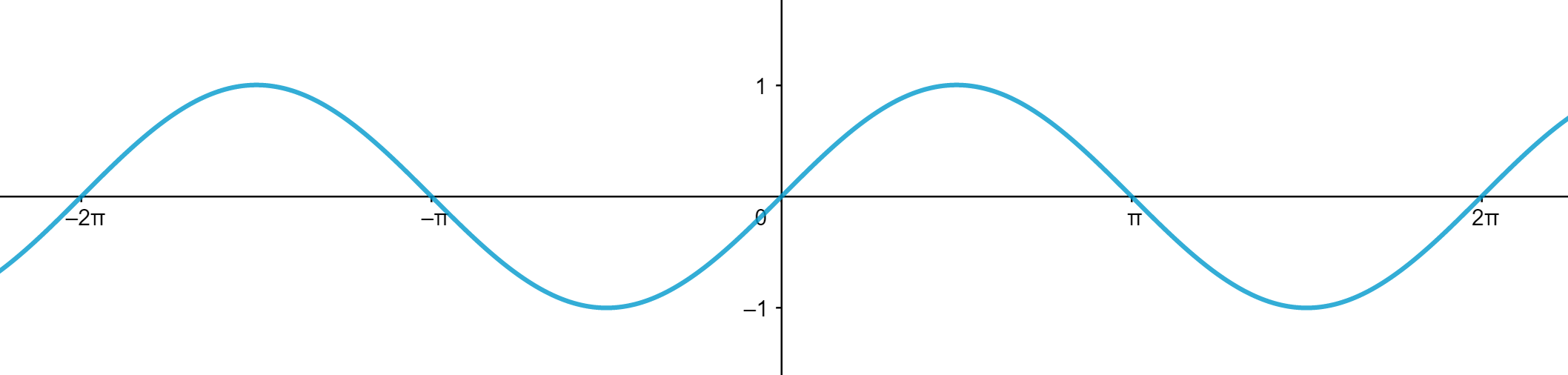
a. Périodicité

$\Rightarrow$$\Rightarrow$ la fonction sinus possède une période $T=2\pi$$T=2\pi$

b. Parité

$\Rightarrow$$\Rightarrow$ la fonction sinus est impaire.

c.

1.4.2 Fonction cosinus

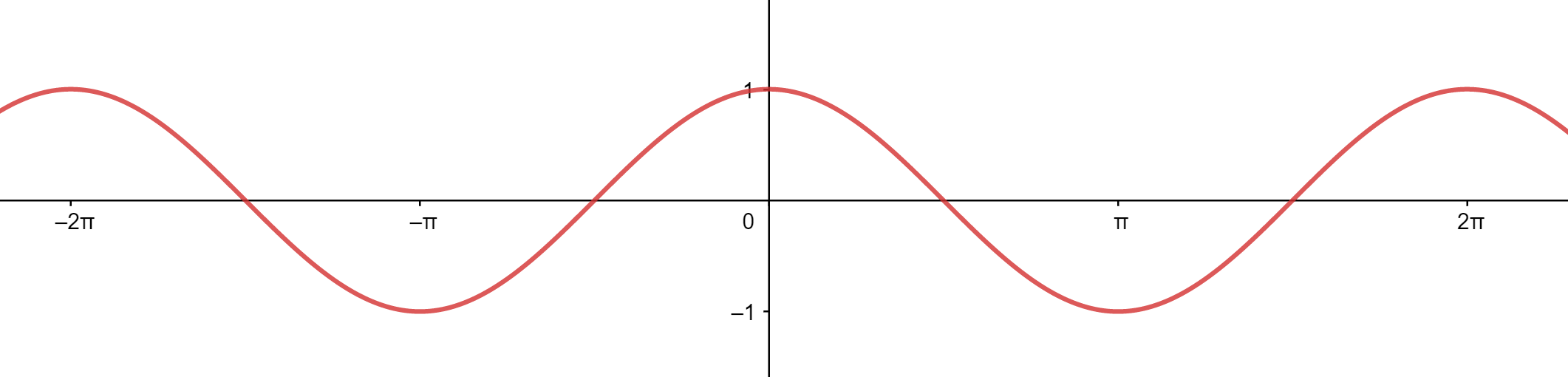
a) Périodicité

$\Rightarrow$$\Rightarrow$ La fonction cosinus possède une période $T=2\pi$$T=2\pi$

b) Parité

$\Rightarrow$$\Rightarrow$ La fonction cosinus est paire.

c)

1.4.3 Fonction tangente

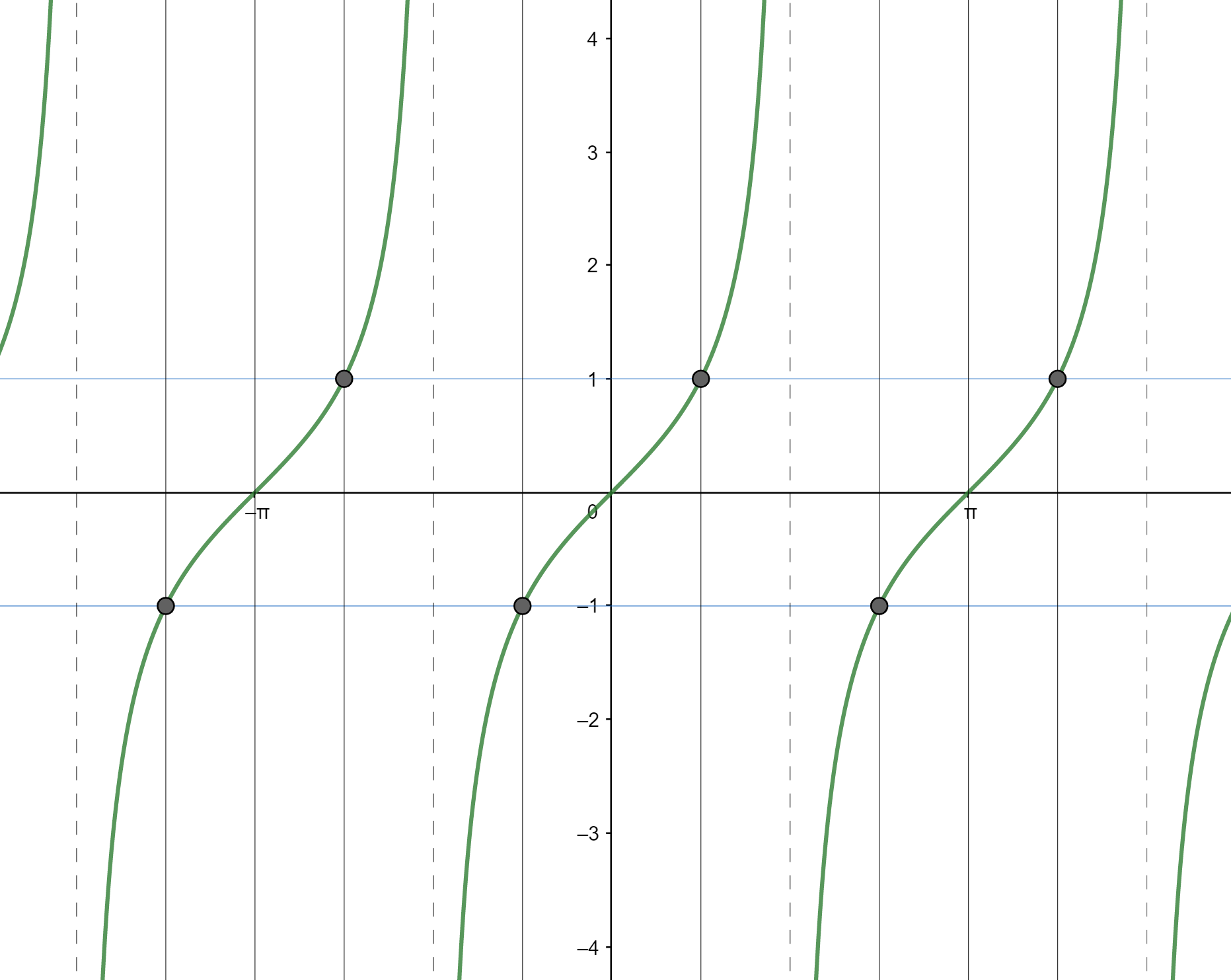
a) Périodicité

$\Rightarrow$$\Rightarrow$ La fonction tangente possède une période $T=\pi$$T=\pi$

b) Parité

$\Rightarrow$$\Rightarrow$ La fonction tangente est impaire.

c)

1.4.4 Passage sinus ↔ cosinus

On peut voir sur les graphes des fonctions qu'il y a un décalage de $\frac{\pi }{2}$$\frac{\pi}{2}$ entre la fonction sinus et cosinus. En en déduit alors :

1.5 Fonction trigonométriques inverses

Pour définir les fonction trigonométriques inverses, il est nécessaire de restreindre les domaines de définition, car il existe un infinité de solution pour un même angle.

1.5.1 Fonction sinus inverse

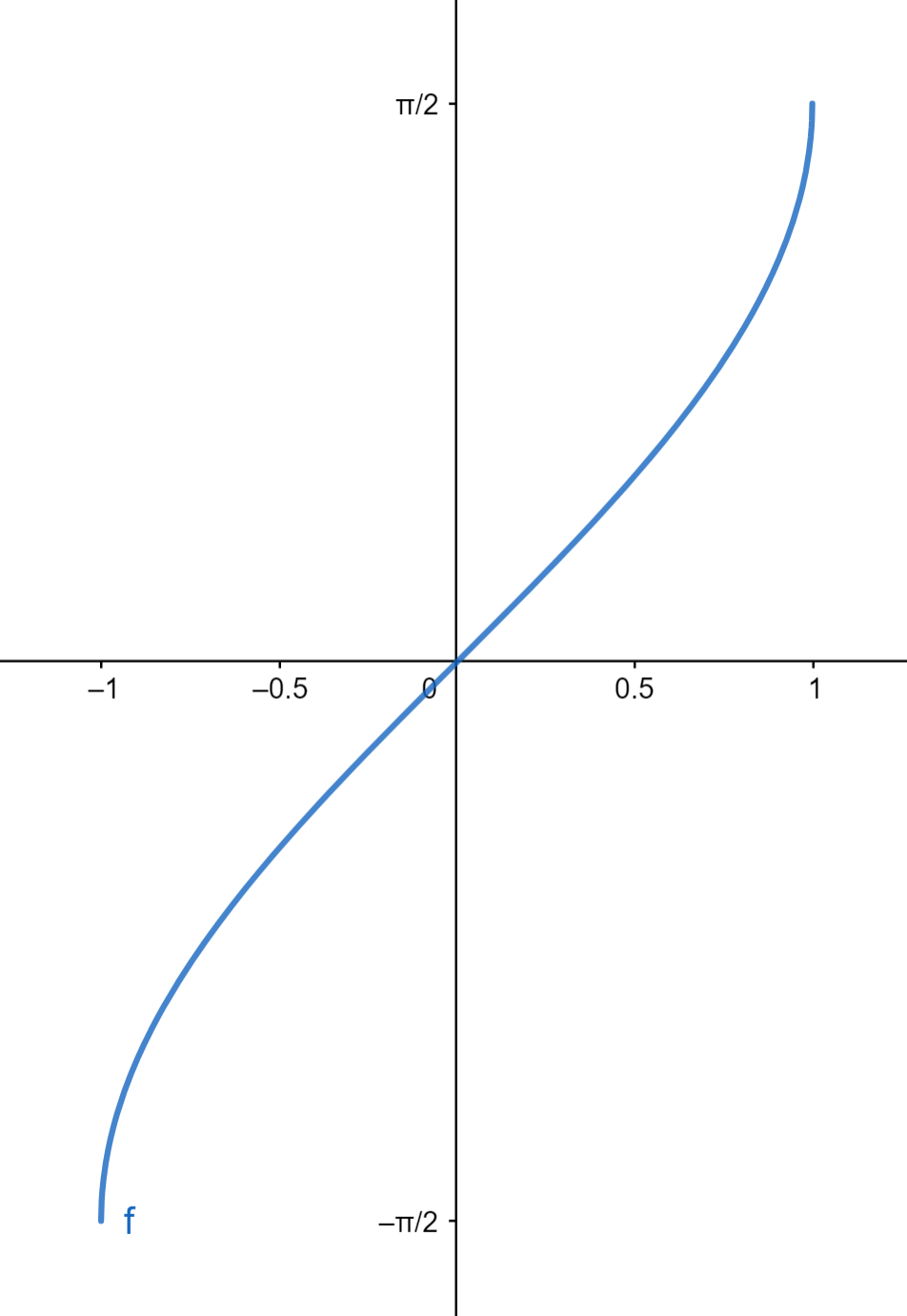
1.5.2 Fonction cosinus inverse

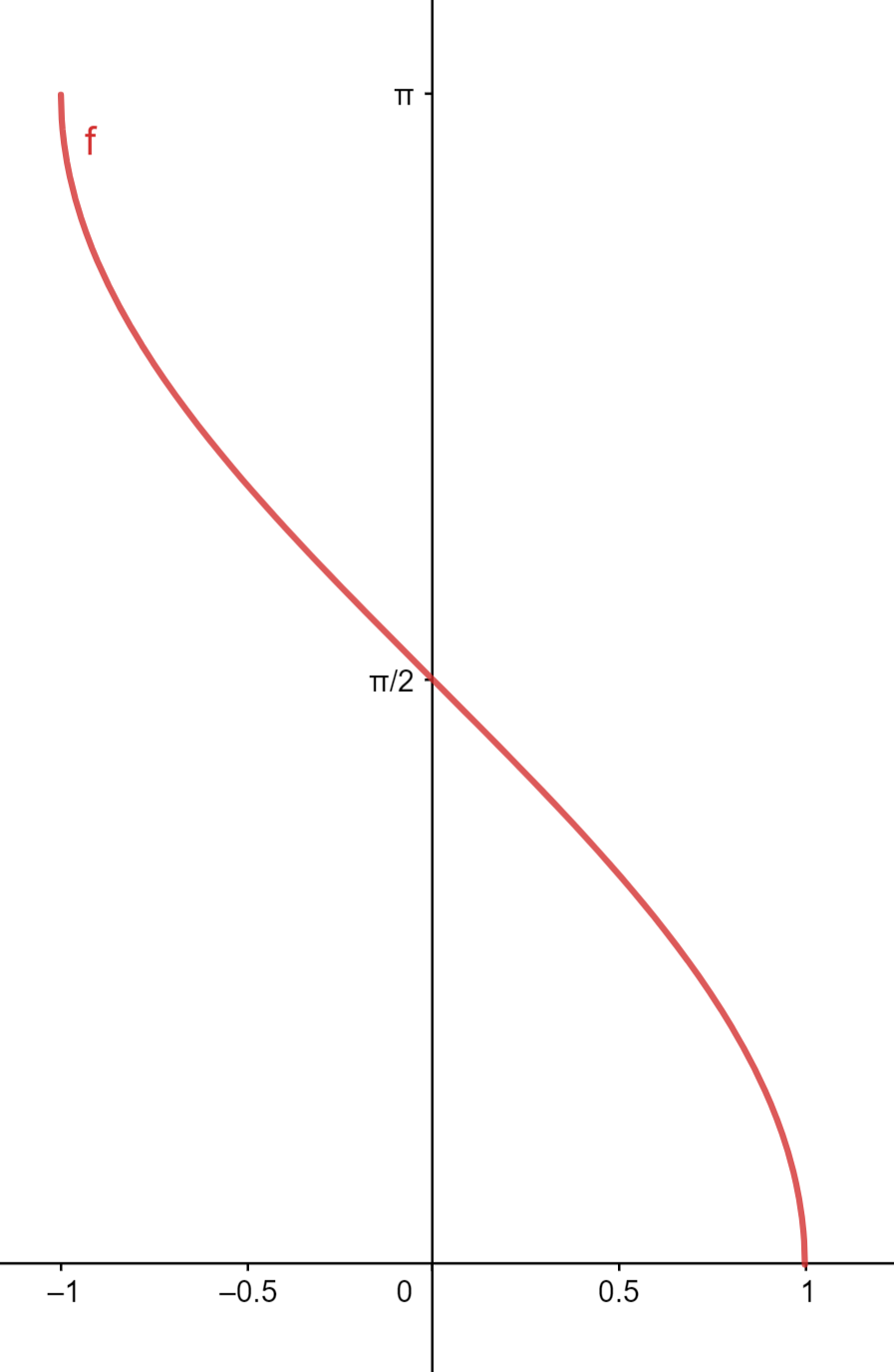
1.5.3 Fonction tangente inverse

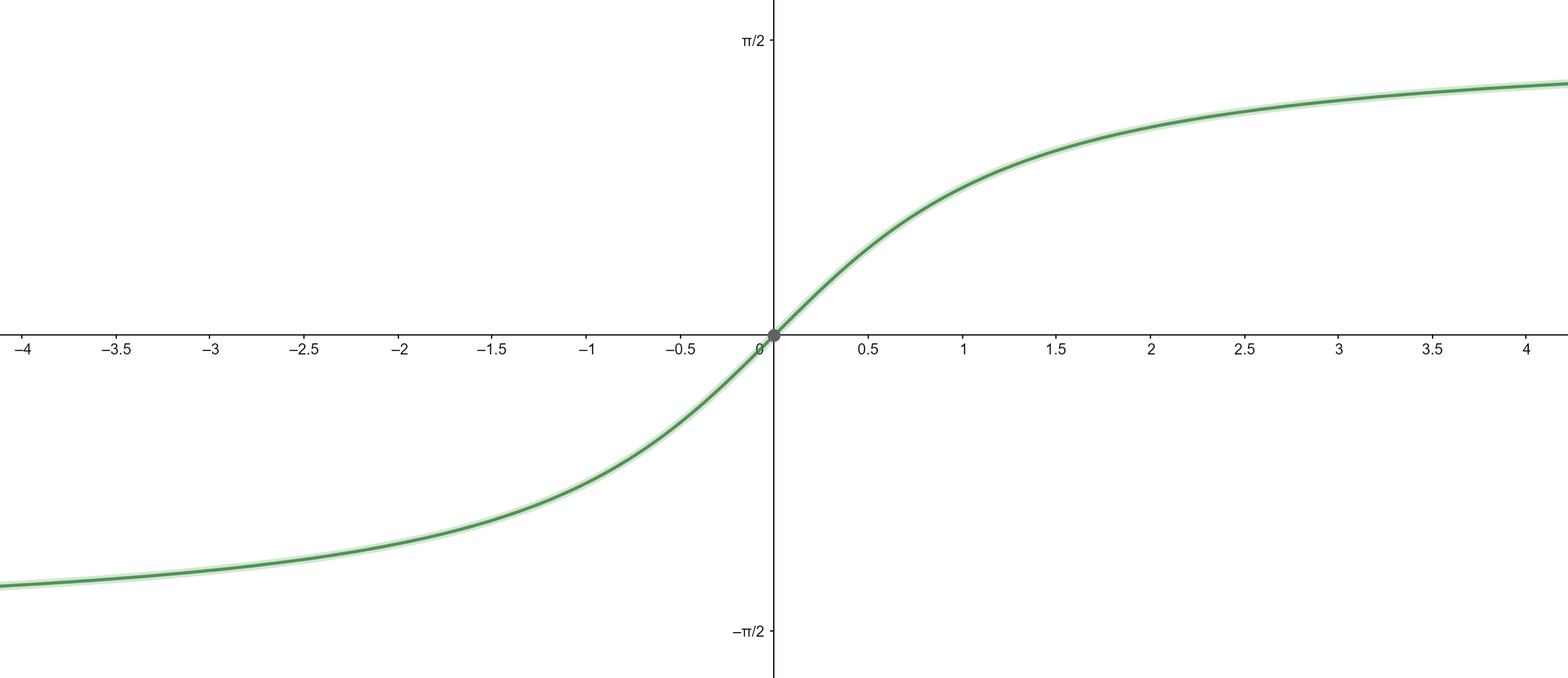
1.6 Fonctions trigonométriques généralisées

→ les exemples sont fait avec la fonction sinus mais sont également valables pour toutes les autres fonctions trigonométriques.

1.6.1 Dilatation et compression verticale

• la multiplication de $\sin \left(x\right)$$\sin(x)$ par un facteur $A\in \mathbb{R}$$A \in \R$ change uniquement l'amplitude de son graphe
• La position verticale ainsi que la période ne changent pas.

1. $y=A\cdot \sin \left(x\right),A>1\Rightarrow$$y = A \cdot \sin(x), \space A>1 \Rightarrow$ dilatation verticale d'un facteur $A$$A$.
2. $y=A\cdot \sin \left(x\right),0<A<1\Rightarrow$$y = A \cdot \sin(x), \space 0<A<1 \Rightarrow$ compression verticale d'un facteur $A^{-1}$$A^{-1}$

1.6.2 Dilatation et compression horizontale

• la multiplication de $x$$x$ par un facteur $\alpha \in \mathbb{R}$$\alpha \in \R$ change uniquement la période de la fonction.

• La position et l'amplitude ne changent pas

1. $y=\sin (\alpha \cdot x),\alpha >1\Rightarrow$$y = \sin(\alpha \cdot x), \space \alpha>1 \Rightarrow$ compression horizontale, division de la période par un facteur $\alpha$$\alpha$ : $T=2\pi \cdot {\alpha }^{-1}$$T = 2\pi \cdot \alpha^{-1}$
2. $y=\sin (\alpha \cdot x),0<\alpha <1\Rightarrow$$y = \sin(\alpha \cdot x), \space 0<\alpha<1 \Rightarrow$ dilatation horizontale, multiplication de la période par un facteur ${\alpha }^{-1}$$\alpha^{-1}$ : $T=2\pi \cdot {\alpha }^{-1}$$T = 2\pi \cdot \alpha^{-1}$

1.6.3 Translation verticale

En ajoutant une constante $b$$b$ à la fonction $\sin \left(x\right)$$\sin(x)$, on obtient une translation verticale du graphe dans le sens du signe de $b$$b$.

• $y=\sin \left(x\right)+b,b>0\Rightarrow$$y = \sin(x) + b, \space b>0 \Rightarrow$ translation verticale de $b$$b$ unités vers le haut
• $y=\sin \left(x\right)+b,b<0\Rightarrow$$y = \sin(x) + b, \space b<0 \Rightarrow$ translation verticale de $b$$b$ unités vers le bas

1.6.4 Translation horizontale

En ajoutant une constante $\phi$$\varphi$ à la variable $x$$x$, on obtient une translation horizontale du graphe dans le sens inverse du signe de $\phi$$\varphi$.

• $y=\sin (x-\phi ),\phi >0\Rightarrow$$y=\sin(x-\varphi), \space \varphi >0 \Rightarrow$ translation horizontale de $\phi$$\varphi$ unités vers la droite.
• $y=\sin (x-\phi ),\phi <0\Rightarrow$$y=\sin(x-\varphi), \space \varphi <0 \Rightarrow$ translation horizontale de $\phi$$\varphi$ unités vers la gauche.

1.6.5 Définition générale / nomenclature

Soit $y=A\cdot \sin (\alpha x-\phi )+b$$y = A \cdot \sin(\alpha x - \varphi) + b$, on nomme alors :

1.7 Equations trigonométriques

1.7.1 Equation de base

Equation du type $A\cdot \cos (\alpha x-\phi )+b=c$$A \cdot \cos(\alpha x - \varphi) + b = c$

Les solutions d'une équation du type $\cos \left(x\right)=c$$\cos(x) = c$ sont :

avec $c\in [-1,1]$$c \in \left[ -1,1 \right]$

Si cette condition n'est pas respectée, l'équation n'admet aucune solution. (En effet, aucune valeur d'angle ne donne un cosinus non-compris entre -1 et 1)

On a alors

On résout ensuite l'équation de cette manière :

Equation du type $A\cdot \sin (\alpha x-\phi )+b=c$$A \cdot \sin(\alpha x - \varphi) + b = c$

Les solutions d'une équation du type $\sin \left(x\right)=c$$\sin(x) = c$ sont :

avec $c\in [-1,1]$$c \in \left[ -1,1 \right]$

Si cette condition n'est pas respectée, l'équation n'admet aucune solution. (En effet, aucune valeur d'angle ne donne un sinus non-compris entre -1 et 1)

On a alors

On résout ensuite l'équation de cette manière :

Equation du type $A\cdot \tan (\alpha x-\phi )+b=c$$A \cdot \tan(\alpha x - \varphi) + b = c$

Les solutions d'une équation du type $\tan \left(x\right)=c$$\tan(x) = c$ sont :

Il n'y pas de restrictions sur $c$$c$, en effet, le domaine de définition de la fonction $\arctan$$\arctan$ vaut $\mathbb{R}$$\R$ .

On résout l'équation de cette manière :

1.7.2 Equation de la forme $f(\sin \left(x\right))=0$$f(\sin(x)) = 0$

La résolution est la même avec les autres fonctions trigonométriques.

C'est une équation qui est fonction du sinus (ou cos, tan, ...).

Par exemple :

L'équation est dans ce cas fonction de $\sin \left(2x\right)$$\sin(2x)$.

Pour résoudre ce type d'équation, il faut effectuer un changement de variable. On remplace la fonction trigonométrique par $u$$u$ (Dans l'exemple, on pose $u=\sin \left(2x\right)$$u = \sin(2x)$).

Désormais, il faut résoudre l'équation de type 2^e degré en $u$$u$.

On trouve alors les solutions $u_1,u_2,...,u_n$$u_1,u_2,...,u_n$

On reprend alors le changement de variable et on résout comme une équation trigonométrique de base en posant $u_i=\sin \left(2x_i\right)$$u_i = \sin(2x_i)$.

1.8 Théorèmes sur les triangles quelconques

1.8.1 Aire d'un triangle quelconque

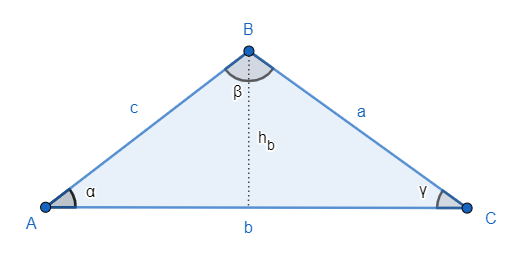
1.8.2 Théorème de l'angle inscrit

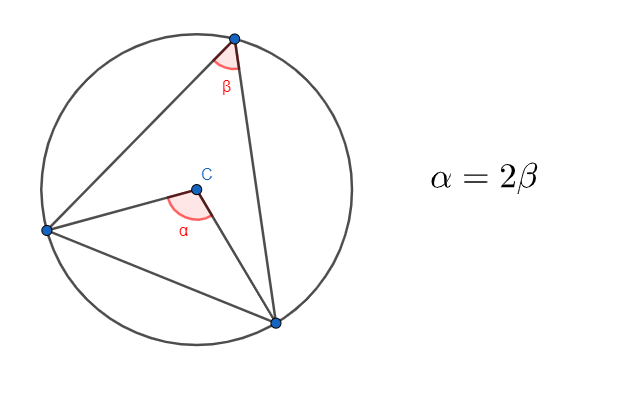
1.8.3 Théorème du sinus

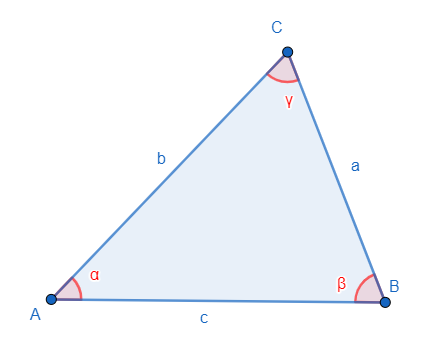
Soit un triangle quelconque $ABC$$ABC$ inscrit dans un cercle de rayon $R$$R$.

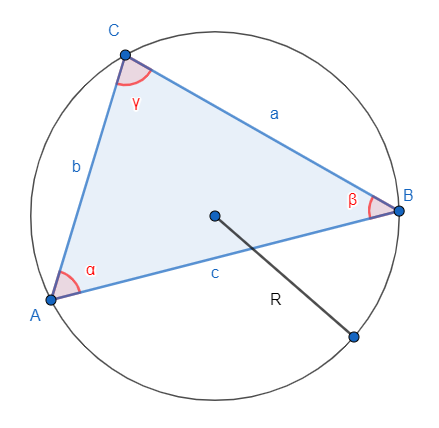
On a alors :

1.8.4 Théorème du cosinus

Soit un triangle quelconque $ABC$$ABC$ :

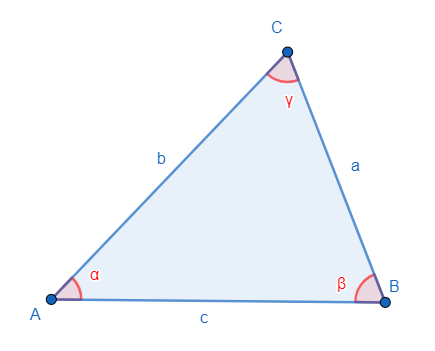
On a alors :

1.8.5 Quand utiliser les différents théorèmes

• On utilise le théorème du sinus quand :

  • On connait deux angles et un côté
  • On connait un angle et deux côté

• On utilise le théorème du cosinus quand :

  • On connait les trois côtés

1.9 Formules trigonométriques

ou identités trigonométriques

Ce ne sont pas des équations mais bien des identités, les graphes d'un côté du signe égal et de l'autre sont les mêmes.

Les deux expressions sont équivalentes.

1.9.1 Formules de base

Ces formules découlent directement des définitions.

1.9.2 Formules simples

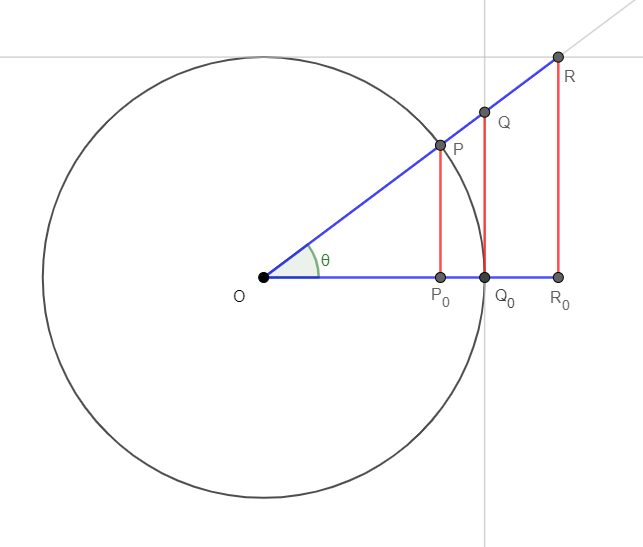
1.9.3 Somme et différence de deux angles

Sinus et cosinus de la somme/différence de deux angles

démonstration

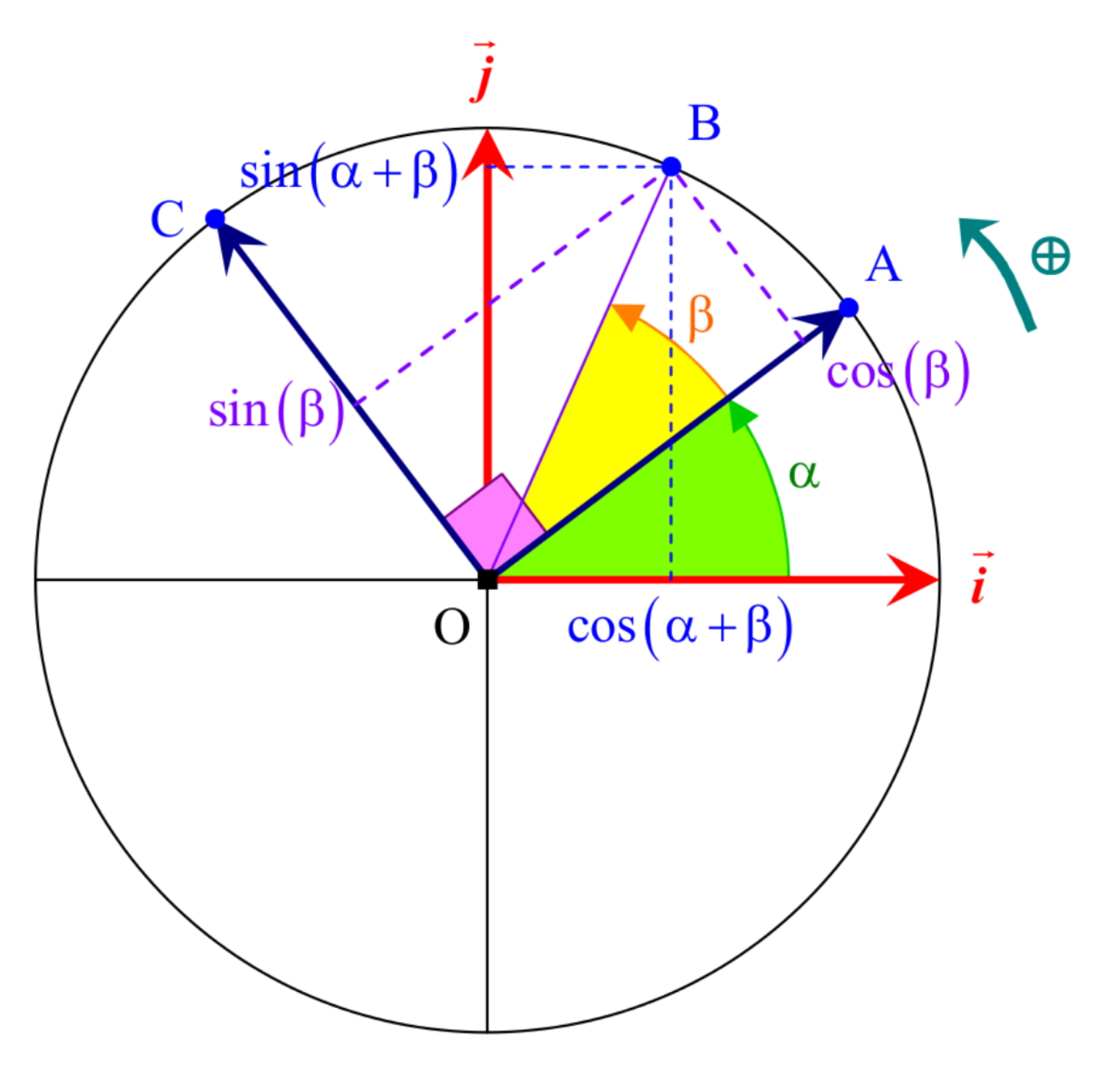
On exprime $\overrightarrow{OB}$$\overrightarrow{OB}$ avec $\overrightarrow{OA}$$\overrightarrow{OA}$ et $\overrightarrow{OC}$$\overrightarrow{OC}$ :

D'après la figure, $\overrightarrow{OB}$$\overrightarrow{OB}$ est aussi :

De ces deux expressions pour $\overrightarrow{OB}$$\overrightarrow{OB}$ on en déduit :

CQFD.

Tangente de la somme/différence de deux angles

1.9.4 Formules des angles doubles

1.9.5 Formules des demis-angles

1.9.6 Transformation produit → somme

1.9.7 Transformation somme → produit