Population : c’est un ensemble d’objets de même nature qui présentent trait caractéristique que l’on souhaite étudier
Individu : un élément unique de la population
Caractère : une des valeurs ou modalité qu’on évalue.
Un caractère est dit qualitatif s’il représente une qualité. C’est le cas quand la réponse donnée est un mot ou une expression.
Un caractère est dit qualitatif ordinal s’il existe une relation d’ordre entre les différentes valeurs possibles et il est dit qualitatif nominal si ce n’est pas le cas.
Un caractère est dit quantitatif s’il représente une quantité. C’est le cas quand la réponse donnée est un nombre.
Un caractère est dit quantitatif discret si la réponse donnée est un nombre naturel et il est dit quantitatif continu si la réponse donnée peut prendre n’importe quelle valeur dans un intervalle donné.
\[ \boxed{ \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i } \]
Attention : La moyenne est très sensible aux valeurs extrêmes, au point qu’elle peut en perdre de sa représentativité !
Ce sont des mesures de dispersion.
La variance est donnée par :
\[ \boxed{ v = \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2 } \]
L’écart-type quant à lui, est égal à la racine carrée de la variance :
\[ \boxed{ \sigma = \sqrt{v} = \sqrt{\frac{1}{n}\sum_{i=1}^n (x_i - \overline{x})^2} } \]
Ces mesures permettent d’évaluer à quel point les mesures s’éloignent de la moyenne \(\overline{x}\).
C’est une mesure de la tendance centrale. La médiane est la valeur qui divise la population en deux parts égales.
Pour la calculer, il faut d’abord trier la série \(X\) par ordre croissant, pour former la série \(\tilde{X}\) telle que :
\[ \tilde{X} : \tilde{x}_1 \leq \tilde{x}_2 \leq \cdots \leq \tilde{x}_{n-1} \leq \tilde{x}_n \]
Ensuite, il suffit de choisir la valeur qui se trouve au milieu. Dans le cas où \(n\) est pair, on prend alors la moyenne des deux valeurs centrales comme valeur de médiane :
Si \(n\) est impair :
\[ m_e = \tilde{x}_{\frac{n+1}{2}} \]
Si \(n\) est pair
\[ m_e = \frac{\tilde{x}_{\frac{n}{2}} + \tilde{x}_{\frac{n}{2}+1}}{2} \]
La médiane n’est pas affectée par les valeurs extrêmes.
C’est une mesure de dispersion.
Sa valeur est donnée par la moitié de la longueur de l’intervalle compris entre les quartiles \(Q_1\) et \(Q_3\) :
\[ isi = \frac{Q_3-Q_1}{2} \]
Le quartile \(Q_1\) sépare les quart des plus petites valeurs de la population des autres tandis que \(Q_3\) sépare le quart des plus grandes valeurs des autres.
La manière de calculer les quartiles est similaire à celle de la médiane.
Il faut commencer par séparer la population en deux ensembles distincts, selon la médiane (si \(n\) impair, la médiane appartient au deuxième groupe).
Ensuite, \(Q_1\) est donné par la médiane du premier groupe et \(Q_3\) par la médiane du deuxième.
Le mode est la valeur la plus fréquente dans une série de données. Il peut exister plusieurs modes dans une même série.
Par définition, le moment d’ordre \(r\) est donné par :
\[ \boxed{ m_r = \frac{1}{n} \sum_{i=1}^n x_i ^r } \]
et le moment centré d’ordre \(r\) est donné par :
\[ \boxed{ \mu_r = \frac{1}{n}\sum_{i=1}^n (x_i - m_1)^r } \]
On remarque par exemple qu’en réalité la moyenne correspond en réalité au moment d’ordre 1 :
\[ \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i = m_1 \]
De la même manière, il se trouve que la variance correspond au moment centré d’ordre 2 :
\[ \sigma ^2 = {1\over n} \sum _{i=1}^n (x_i - \overline{x})^2 = {1\over n} \sum _{i=1}^n (x_i -m_1)^2 = \mu_2 \]
Quand la série de données contient trop de valeurs différentes ou que la nature du caractère est continue, on regroupe les valeurs selon des classes de même amplitude.
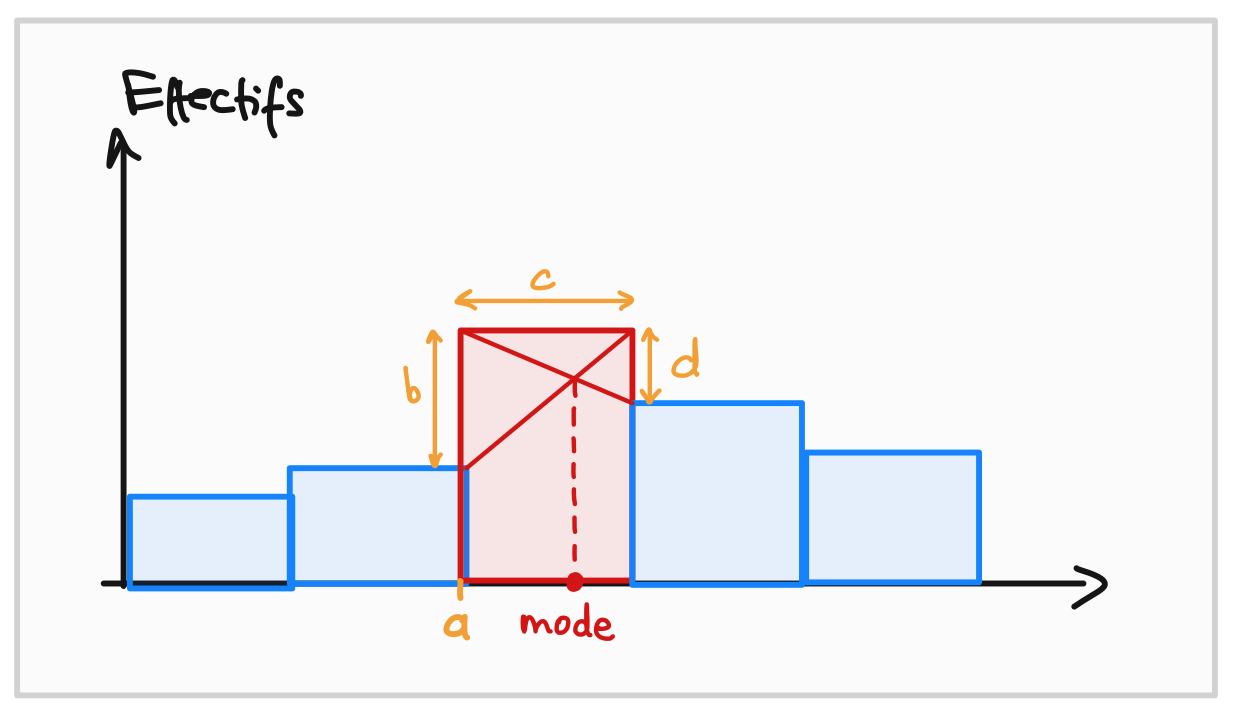
Dans le cas continu, le mode se trouve dans le casse ayant le plus grand effectif (la classe modale). Il se calcule à partir de l’histogramme des effectifs (ou celui des fréquences).

\[ \boxed{ m_o = a + c \cdot \frac{b}{b+d} } \]
La fréquence est la proportion \(f_i\) des individus qui appartiennent à une certaine classe.
Par définition, la fréquence est donnée par :
\[ \boxed{ f_i = \frac{n_i}{n} } \]
où \(n\) est l’effectif total et \(n_i\) l’effectif de la classe en question.
La fréquence cumulée est la proportion \(F(x)\) des individus qui présentes des valeurs inférieures ou égales à \(x\). Elle est calculée en additionnant toutes les fréquences \(f_i\) correspondants aux \(x_i\) tels que \(x_i \leq x\).
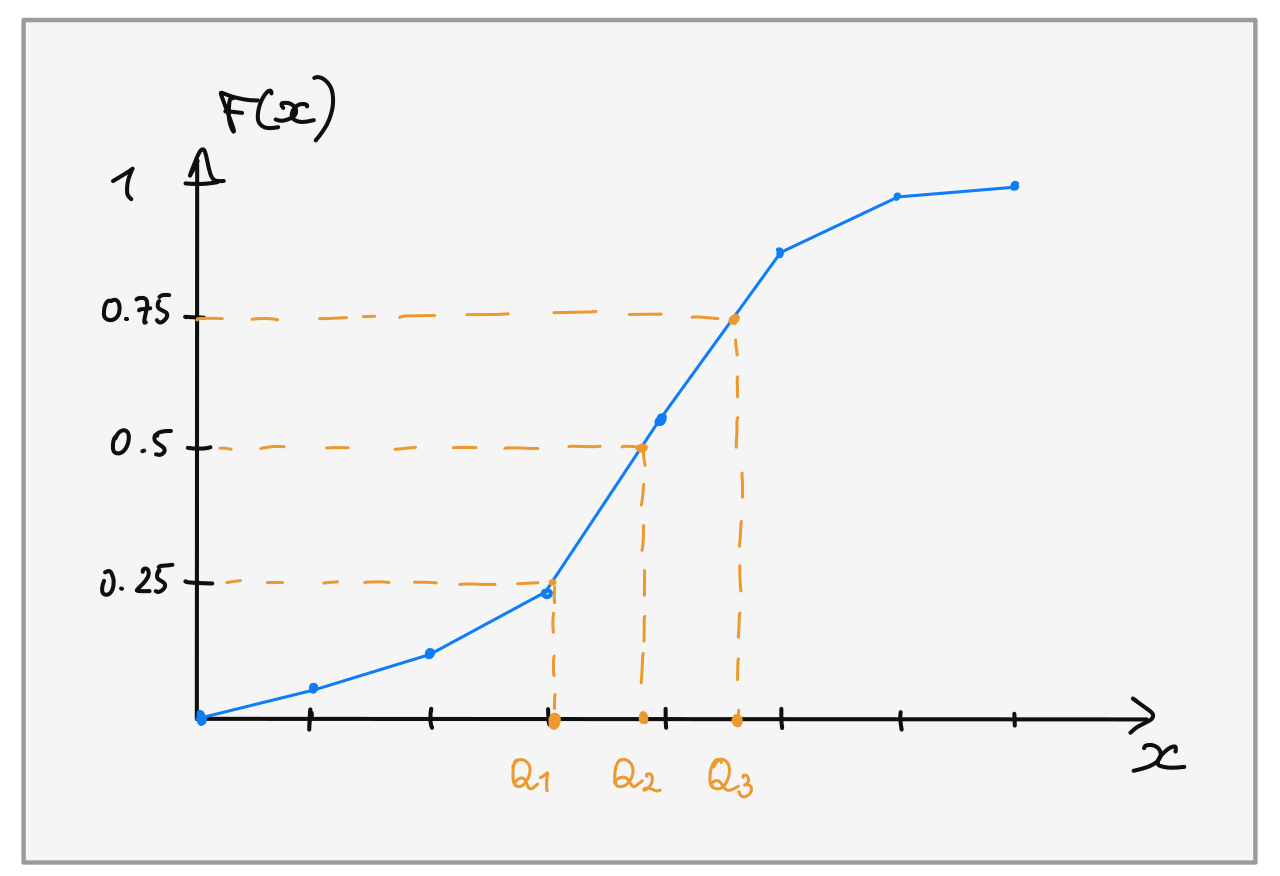
La médiane se calcule à partir du polygone des fréquences cumulées.
Il faut d’abord trouver les segment qui coupe la droite horizontale d’ordonnée \(0.5\), puis on peut en déduire la médiane en effectuant une interpolation linéaire à l’aide du théorème de Thalès.
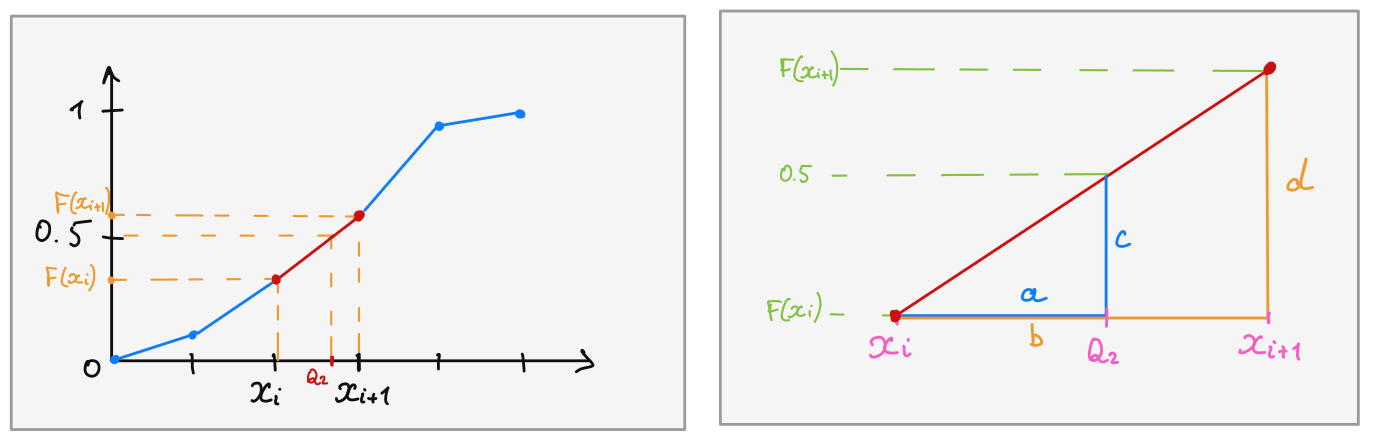
Ainsi, dans le cas général, la médiane est donnée par :
\[ \boxed{ m_e = \frac{0.5 - F(x_i)}{F(x_{i+1}) - F(x_i)} \cdot (x_{i+1} - x_i) + x_i } \]
avec \(x_i\) et \(x_{i+1}\) tels que \(F(x_i) \leq 0.50 \leq F(x_{i+1})\)
Par définition, l’intervalle semi-interquartile est donné par :
\[ \boxed{ isi = \frac{Q_3 - Q_1}{2} } \]
où \(Q_1\) et \(Q_3\) se calculent de manière similaire à la médiane :
\[ Q_1 = \frac{0.25 - F(x_j)}{F(x_{j+1}) - F(x_j)} \cdot (x_{j+1} - x_j) + x_j \]
avec \(x_j\) et \(x_{j+1}\) tels que \(F(x_j) \leq 0.25 \leq F(x_{j+1})\)
\[ Q_3 = \frac{0.75 - F(x_k)}{F(x_{k+1}) - F(x_k)} \cdot (x_{k+1} - x_k) + x_k \]
avec \(x_k\) et \(x_{k+1}\) tels que \(F(x_k) \leq 0.75 \leq F(x_{k+1})\)
Dans le cas continu, on calcule la moyenne et l’écart type de la même manière que dans le cas discret en prenant les valeurs des centres des classes.
Ces mesures vont alors légèrement varier selon la manière dont sont formées les classes.
Si on utilise la moyenne comme mesure de la tendance centrale, il faut utiliser l’écart-type comme mesure de dispersement tandis que si on utilise plutôt la médiane comme mesure de la tendance centrale, il faut utiliser l’intervalle semi-interquartile comme mesure de dispersion.
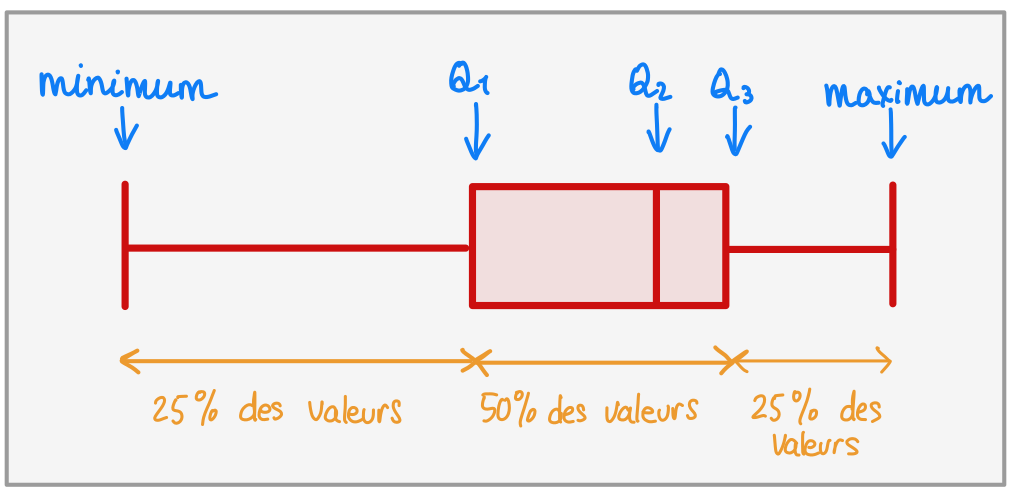
La boîte à moustache est une manière rapide de représenter le profil essentiel d’une série statistique.
Elle résume certaines caractéristiques du caractère étudié, tels que la médiane, le maximum, le minimum, etc.
L’asymétrie évalue si la distribution est, par rapport à une valeur centrale, plus étalée à gauche ou à droite, ou si au contraire, les observation sont équitablement réparties autour de la valeur centrale. Quand une distribution est asymétrique, les valeurs centrales telle que la moyenne, la médiane et le mode ne sont plus confondues au centre de la distribution comme c’est le cas pour une distribution symétrique.
Il existe plusieurs mesures d’asymétries dont les principales sont les suivantes :
\[ \boxed{ \gamma_1 = \frac{\mu_3}{\sigma^3} = \frac{\mu_3}{\sqrt{\mu_2^3}} } \]
\[ \boxed{ \beta_1 = 3\cdot \frac{\overline{x} - m_e}{\sigma} } \]
\(\beta_1\) est généralement compris entre \(-1\) et \(1\).
\[ \boxed{ c_{y} = \frac{Q_3 + Q_1 - 2\cdot m_e}{Q_3 - Q_1} } \]
Dans le cas d’une distribution symétrique on a que \(\gamma_1, c_y = 0\) et que \(\beta_1\) tend vers \(0\).
De plus, \(m_o = m_e = \overline{x}\).
Dans le cas d’une distribution étalée à droite, on a que \(\gamma_1, c_y > 0\) et que \(\beta_1\) tend vers \(1\).
De plus, \(m_o < m_e < \overline{x}\)
Dans le cas d’une distribution étalée à gauche, on a que \(\gamma_1, c_y < 0\) et que \(\beta_1\) tend vers \(-1\).
De plus, \(m_o > m_e > \overline{x}\)
Le coefficient \(\gamma_2\) de Fisher (ou Kurtosis) est donné par :
\[ \boxed{ \gamma_2 = \frac{\mu_4}{\sigma^4} -3 } \]
Dans le cas où \(\gamma_2 >0\), la distribution est dite leptokurtique et elle a une forme de pointe (elle s’élève assez haut et retombe brutalement).
Dans le cas où \(\gamma_2 < 0\), la distribution est dite platykurtique et elle a une forme aplatie (elle possède des queues épaisses).
Finalement, dans le cas où \(\gamma_2 \cong 0\), la distribution est dite mesokurtique.
Exported with pandoc 2.9.2.1 on Sun Nov 06 2022 at 17:29:01 CET. @ylked
All informations are given without warranty. All rights reserved ©